정규분포

이미지 출처: https://www.mathsisfun.com/data/standard-normal-distribution.html

정규분포는 평균 μ을 기점으로 분산이 σ인 대칭을 띄는 종 모양의 그래프이다.

특히 평균 0, 분산이 1 인 정규분포를 표준정규분포라고 한다.

표준화

표준정규분포가 아닌 일반 정규분포를 평균이 0, 분산이 1이 되도록 맞추어 표준정규분포 형태로 바꾸는 것이다.

μ 가 데이터들의 평균이고, σ가 데이터들의 표준편차일 때, 표준화는 다음과 같이 진행된다.

중심 극한 정리

모딥단이 정규분포를 따르지 않는 표본이더라도, 표본들의 수가 30개 이상이면 근사적으로 정규분포를 따른다는 이론이다. (모분산을 모르는 경우에도, 표본의 수 n이 30 이상인 경우 정규분포를 사용한다.)

표본의 크기가 클수록 모집단의 평균에 근사하는 정규분포 형태를 띄게 된다.

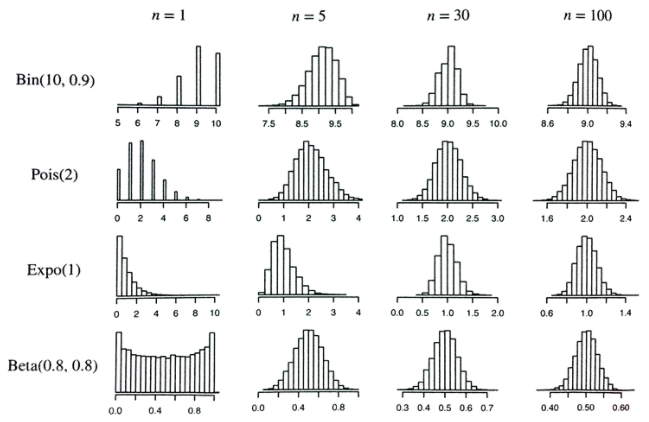
이미지 출처: https://m.blog.naver.com/mykepzzang/220851280035

t 분포

t=0을 중심으로 하는 좌우대칭형 그래프이다.

모집단이 정규분포이지만, 표본의 크기가 30보다 작은 경우에 t 분포를 사용한다. (모분산을 모르는 경우에도 t 분포를 사용하기도 한다.)

따라서 표본의 크기 n이 무한대로 발산하게 되면, 표준 정규분포와 일치하게 된다.

표본 비율의 정규 분포

성공 또는 실패의 두 가지로만 구분되는 이항분포를 따르는 모집단의 표본의 수 n이 충분히 큰 경우, 중심극한정리에 의하여 확률 $\hat{p}=x/n$ 은 근사적으로 정규분포를 따른다. (일반적으로 np>5, nq>5 일 때 n이 충분히 크다고 본다. )

이때 p는 어떤 사건이 일어날 확률이며 q는 일어나지 않을 확률로, 이 둘을 더하면 1이 된다. (p+q=1)

크기가 n인 표본을 추출하여 성공횟수가 x라 할 때, 이를 표본비율이라고 하며 $\hat{p}=\frac{x}{n}$와 같이 나타낸다.

표본비율의 평균, 분산의 값은 기존의 모집단인 이항분포의 평균($E(X)=np$), 분산($Var(X)=npq$)를 이용하여 다음과 같이 계산할 수 있다.

신뢰구간

표본을 통해 추정한 모수를 통해 실제 모수가 있을 구간을 추정한 것이다.

따라서 해당 구간내에 실제 모수가 있을 확률인 신뢰수준을 몇으로 잡느냐에 신뢰구간이 달라진다.

일반적으로 95%와 99%의 신뢰수준을 가질 경우에 대해 신뢰구간을 추정하는 경우가 많다.

신뢰구간은 (하한값, 상한값) 의 형태로 나타낸다. 이는 실제 모수가 하한값 이상과 상한값 이하의 사이에 들어올 것이라고 예상한 것이다.

따라서 모비율 p에 대한 (1-α)*100% 신뢰구간은 다음과 같이 계산된다.

이때 α는 유의수준으로 1종 오류를 범할 최대확률이다.

• 1종 오류: 귀무가설이 맞는데 대립가설을 맞다고 한 경우(연구자가 주장하고자 하는게 대립가설)

또한, 위 식에서 $z_{\frac{\alpha}{2}}\sqrt{\frac{\hat{p}\hat{q}}{n}}$ 은 표본 비율이 모비율과 다를 수 있는 차이인 오차를 나타내는 값이라고 하여, 표본오차라고 불린다. (허용오차, 최대허용오차, 오차범위, 오차한계라고도 불린다.)