행렬(matrix)

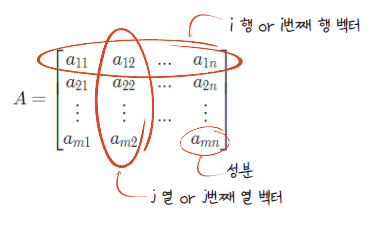
행렬 A의 크기 : m x n (행 개수 x 열 개수)
이러한 행렬 A를 m by n 행렬 또는 m by n matrix 라고 한다.

특히, m = n 일 때의 행렬 A를 n차의 정사각행렬이라고 한다.

$a_{ij}$ 에서 i는 행 번호, j는 열 번호를 의미한다. 이때 $a_{ij}$를 행렬 A의 (i, j) 성분 이라고 한다.

이때 i = j인 성분들을 주대각선 성분이라고 한다. (e.g., $a_{11}$, $a_{22}$, $a_{33}$, ... , $a_{nn}$)

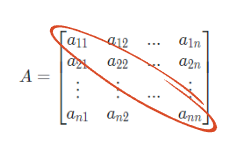
행렬의 연산

[용어 정리]
상등 : 크기가 같은 두 행렬 A, B가 모든 i, j에 대해 $a_{ij}$ = $b_{ij}$일 때 (즉, 모든 성분이 동일한 값을 가질 때), 두 행렬은 서로 같다고 하고, A = B라고 한다.

행렬의 합

A + B = $[a_{ij}+b_{ij}]_{mn}$
각 위치들에 대해서 해당 값들을 상수 덧셈과 동일하게 하면 된다.

※ 행렬의 크기가 같아야 합 연산이 가능하다.

스칼라 배

kᆞA = $[k\cdot a_{ij}]_{mn}$
각 위치들에 대해서 해당 값들을 상수 곱셈과 동일하게 하면 된다.

행렬의 곱

AB = $[c_{ij}]_{mn}$
이때 A = $[a_{ij}]_{m\times p}$ , B = $[b_{ij}]_{p\times n}$이며,
AB = $[c_{ij}]_{mn}$에서 $c_{ij}$는 $a_{i1}b_{1j}+a_{i2}b_{2j}+...+a_{ip}b_{pj}$이다.

※ 행렬 A와 B의 크기에 주의하자. 행렬 A의 크기는 m x p, 행렬 B의 크기는 p x n이다.
즉, 앞에서 곱해지는 행렬의 열의 개수와 뒤에서 곱해지는 행렬의 행의 개수가 서로 같아야 함을 유의하자.

행렬의 곱을 좀 더 직관적으로 이해를 하기위해 다음의 그림을 보자.

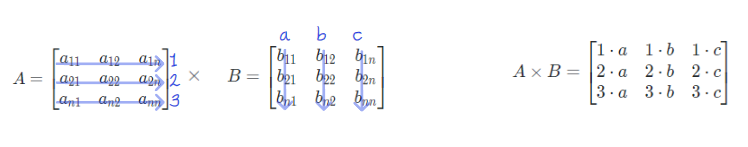
여기서 1ᆞa = $\sum_{i=1}^{3} a_{1i}\times b_{i1}$ = $a_{11}\times b_{11}+a_{12}\times b_{21}+a_{13}\times b_{31}$ 로 계산이 되는 것이다.

$c_{ij}$가 $a_{i1}b_{1j}+a_{i2}b_{2j}+...+a_{ip}b_{pj}$인 것을 위의 행렬 상의 위치와 대조하며 따라가 보면, 보다 쉽게 이해할 수 있다.

<행렬 연산의 기본 성질>
이때 A, B, C는 행렬이며, a, b는 스칼라이다.
1) A+B = B+A
2) A+(B+C) = (A+B)+C
3) A(BC) = (AB)C
4) A(B+C) = AB+AC
5) (B+C)A = BA+CA
6) a(B+C) = aB+aC
7) (a+b)C = aC+bC
8) (ab)C = a(bC)
9) a(BC) = (aB)C = B(aC)

행렬의 거듭제곱

[용어 정리]
단위행렬 ($I_n$) : 주대각선 성분이 모두 1이고, 나머지 성분이 모두 0인 n차 정사각행렬

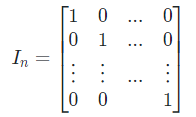
이때 $A^k$ = $A_1A_2 ... A_k$일 때, $A^0$ = $I_n$로 표현된다.
마치 실수에서 $a^0$ = 1인 것과 비슷하게 생각할 수 있다.

👉 단위행렬의 성질 (A가 m x n 행렬일 때)
$I_mA$ = $AI_n$ = $A$

<행렬 거듭제곱의 지수법칙>
1) $A^rA^s$ = $A^{r+s}$
2) $(A^r)^s$ = $A^{rs}$