[백준] 1010. 다리 놓기

김규민·2025년 9월 12일

백준

알고리즘 문제풀이

목록 보기

12/13

다리 놓기

배경 아이디어

처음 문제를 읽었을 때는 다리를 겹치지 않게 배치한다는 말에 빠져서 왼쪽 사이트를 기준으로 문제를 해결하려고 생각했다.

문제 풀이의 편의를 위해 왼쪽 사이트(이하 lsite)와 오른쪽 사이트(이하 rsite)로 부르기로 한다.
또한, 모종의 순서를 부여하여 각 사이트를 생각하도록 한다.

왼쪽 사이트를 기준으로 변수를 선언하고, 경우의 수를 계산하기 위해서는 현재 계산 중인 lsite가 선택할 수 있는 rsite에 대해 기록하고, 그 다음 lsite 는 이전의 사이트의 선택에 따라 각각 경우의 수를 계산해야 한다.
이런 방식으로 문제를 생각하다 보니 지나치게 복잡해지는 것을 깨달았다. 무언가 잘못되었다는 걸 깨달았고, 반대로 riste 를 기준으로 생각을 해보았다.

riste 의 입장에서는 lsite 가 어떤 방식으로 다리를 놓아도 lsite 에 의해 선택받지 않은 사이트가 어디인지가 중요하다.

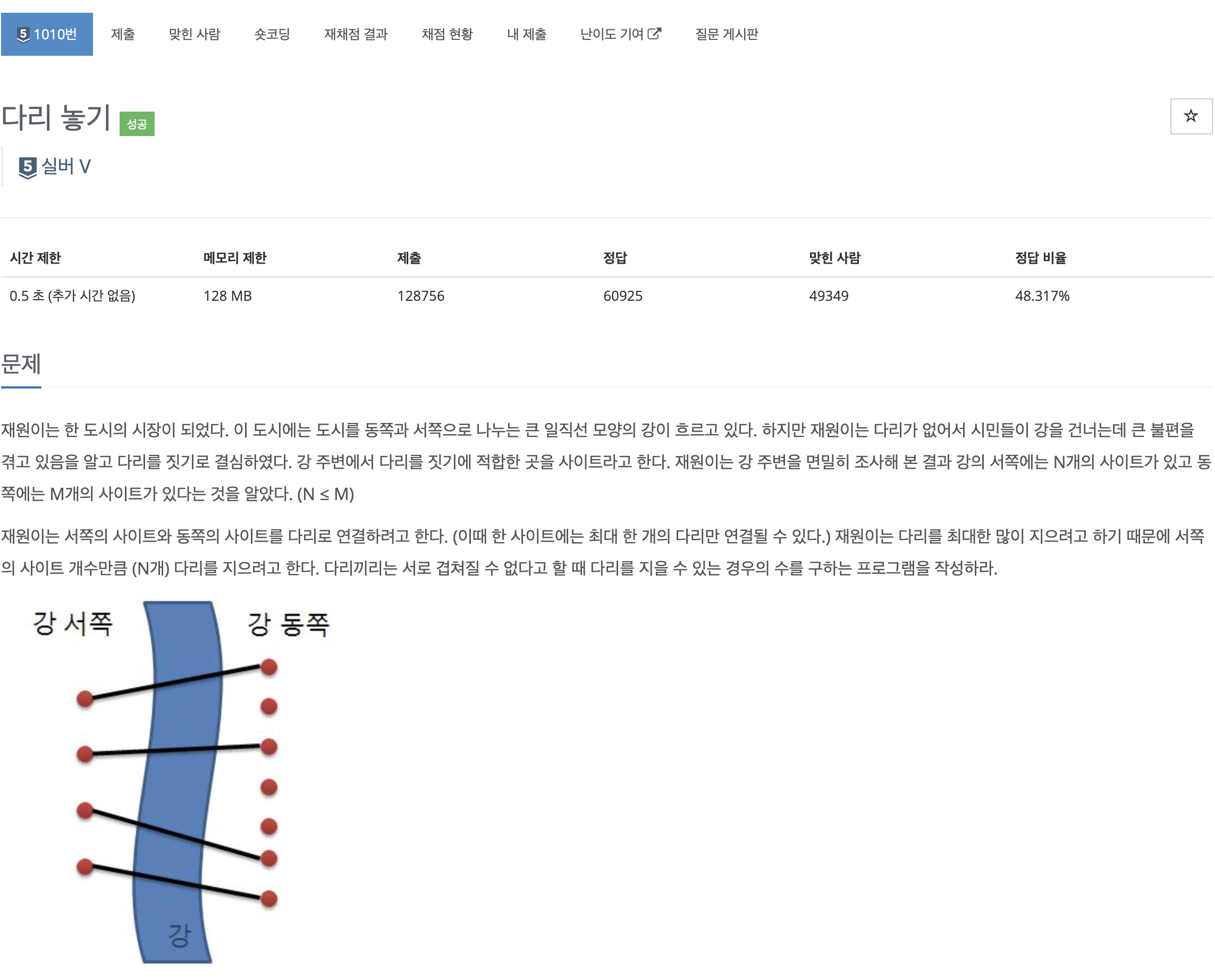
간단한 예시를 통해 이 아이디어를 쉽게 이해할 수 있다.

n = 4, m = 5 라고 하자.
lsite 가 어떤 방식으로 rsite 를 선택하던지,
rsite 의 입장에서 바뀌는 건 몇 번째 사이트가 비어있는지 이다.

예시의 경우에 n과 m의 차이가 1이지만, 그 차이가 1보다 커질 경우에는, m개의 사이트 중 (m-n) 개를 조합하는 경우의 수로 귀결된다.

이때, 앞서 언급했던 "다리를 겹치지 않게 배치해야 한다" 라는 조건이 이 결론에 어떤 영향을 미치는지 확인해야 한다.

다리를 겹치게 지어도 된다면, $m! / (m-n)!$ (ex. 5 x 4 x 3 x 2) 로 계산할 수 있다.
순서를 고려하지 않고, 선택할 수 있는 경우의 수를 모두 고려할 수 있기 때문이다.

하지만 다리를 겹칠 수 없다면, 선택할 수 있는 경우의 수는 이전 lsite 가 선택한 rsite 의 다음 순서들로 제한된다. 이 조건을 반대로 생각하면, 어떤 lsite 가 자기 자신과 다른 순서의 site 를 고를 것인가로 정리된다.

따라서 다리를 겹치지 않게 배치해야 한다는 조건은 결과적으로 선택받지 않은 rsite 의 조합을 고려해야 한다는 전략을 부정하지 않는다.

문제를 해결하는 방법으로 조합의 수를 계산하는 방식을 선택했기 때문에, m개의 site 중 (m-n) 개의 빈 site 를 고르는 조합의 수를 계산해야 한다.
조합의 수 공식은 다음과 같다.

$m!/((m-n)!n!)$

코딩

T = int(input())

def bridge(n, m):
    if n == m: return 1
    if n == 1: return m
    
    r = m - n
    temp = 1
    for i in range(1, r+1):
        temp *= i
    r_pac = temp
    
    not_r = n
    temp = 1
    for i in range(1, not_r+1):
        temp *= i
    not_r_pac = temp
    
    temp = 1
    for i in range(1, m+1):
        temp *= i
    m_pac = temp
    
    return int(m_pac / (r_pac * not_r_pac))

for _ in range(T):
    n, m = map(int, input().split())
    print(bridge(n, m))