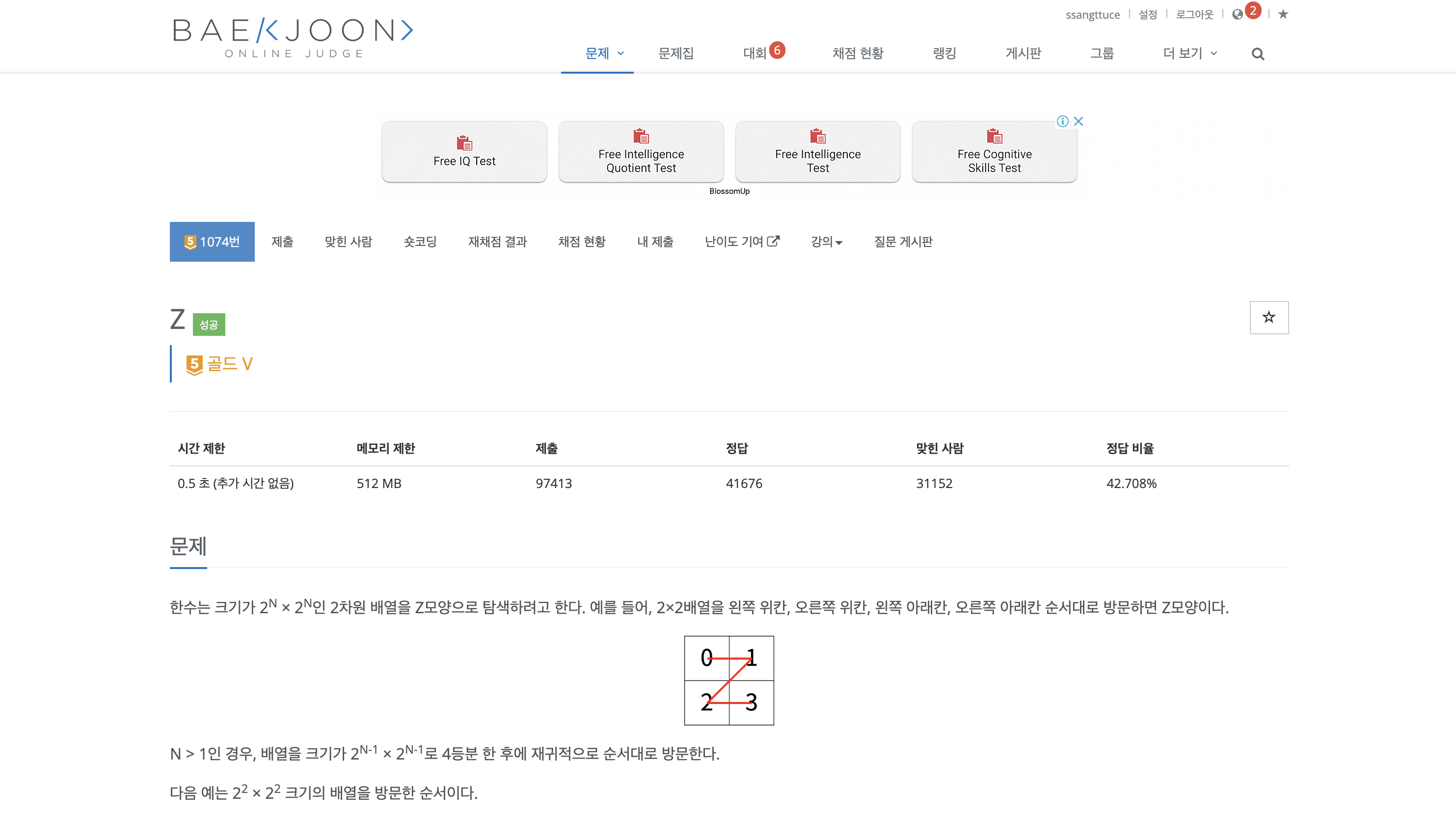
Z

배경 아이디어

문제에서 직접적으로 "재귀" 라는 단어를 사용하였고, "4등분" 이라는 반복적인 구조를 제시하였다.

2차원 배열의 형태

$2^N \times 2^N$ 인 2차원 배열은 사분면으로 나뉘어지는 평면 좌표계의 형태로 바라볼 수 있다. 축의 길이가 $2^N$ 으로 고정되어 있는 자연수 좌표계라고 가정하고 문제를 바라볼 수 있어야 해결할 수 있다.
z 모양으로 방문하는 순서를 활용하여 사분면의 번호를 수학계의 번호와 다르게 매기도록 한다.
왼쪽 위의 사분면을 제 1사분면, 오른쪽 위의 사분면을 제 2사분면, 왼쪽 아래의 사분면을 제 3사분면, 오른쪽 아래의 사분면을 제 4사분면으로 정의한다.

방문 순서의 특징
패턴 자체는 문제에서 직접 언급했지만, 집중해야 하는 부분은 패턴 자체가 아니라 패턴으로 인해 생성되는 방문 순서의 툭징이다.

우선 N = 1 인 경우의 2차원 배열을 통해 순서의 특징을 알아보자.

방문 순서를 따라 수를 매기면,

• 제 1사분면 -> 제 2사분면 의 경우에 1이 증가하고,
• 제 1사분면 -> 제 3사분면 의 경우에 2가 증가하고,
• 제 1사분면 -> 제 4사분면 의 경우에 3이 증가한다.

당연하다고 느껴지지만, 이 패턴을 통해 제 2, 3, 4사분면의 방문 순서는 제 1사분면의 방문 순서에 각각 1, 2, 3 을 더하여 구할 수 있다는 사실을 인지해야 한다.

방문 순서와 N 의 관계
N = 1 인 경우에 각 사분면은 하나의 숫자로 이루어 지지만, 1보다 큰 경우에 전체 배열에 대한 각 사분면은 각각 2차원 배열로 구성된다.

N = 2 인 경우의 2차원 배열의 각 사분면에 대해 확인해보자.
전체 배열에 대한 제 2사분면의 제 1사분면은 4이다.
(이하 2-1사분면)
2-2, 2-3, 2-4사분면은 각각 5, 6, 7이다.
z 모양의 방문 순서가 그대로 유지되는 "재귀적인" 구조이므로, 제 1사분면(N=1 인 2차원 배열과 같다)과 제 2사분면의 방문 순서의 특징은 동일하게 적용되어야 한다.

따라서 1-1 -> 2-1 은 1이 증가되어야 하고, 1-1 -> 3-1 은 2가 증가해야 한다.

재귀적인 규칙 도출
하지만 이 예상은 현실과 다르다. 실제로는 각각 4와 8이 증가한다.
N = 1 인 배열에서 찾았던 사분면의 규칙성은 재귀적인 특징을 만족하지 못 하는 것을 알 수 있다. 규칙이 단순히 1, 2, 3을 더하는 것이 아니라는 것을 알 수 있다.

문제 전체를 아우르는 규칙은 N 과 관련이 있다.
이를 파악하기 위해서는 문제에 제시된 조건을 단계별로 적용해보며 가정했던 규칙을 보완해야 한다.
N 의 경우에 따라 전체 배열에 대한 사분면에 각각 어떤 규칙이 드러나는지 확인해보도록 하자.

• N = 1, 제 1사분면에 1, 2, 3을 더하여 제 2, 3, 4사분면의 방문 순서를 구할 수 있다.
• N = 2, 제 제 1사분면에 4, 8, 12을 더하여 제 2, 3, 4사분면의 방문 순서를 구할 수 있다.
• N = 3, 제 제 1사분면에 16, 32, 48을 더하여 제 2, 3, 4사분면의 방문 순서를 구할 수 있다.

제 2, 3, 4사분면의 방문순서를 구하기 위해 제 1사분면에 더해야 하는 값들의 규칙성을 파악할 수 있다.

$((사분면\space번호)-1)\times2^{(N-1)}\times2^{(N-1)}$

이 수식은 수학에 대한 감각이 좋은 사람이라면 위의 과정이 없이 바로 찾을 수도 있을 것이다.

2차원 배열의 구조를 보고 각 사분면을 한 변의 길이가 $2^{(n-1)}$ 인 정사각형으로 인식한다면 제 1사분면에서 다른 사분면의 방문 횟수를 자연스럽게 생각할 수 있기 때문이다.

코드

def z_order(N, r, c):
    count = 0
    size = 2 ** N
    while size > 1:
        size //= 2
        # 몇 번째 사분면인지 파악
        if r < size and c < size:
            # 1사분면 (왼쪽 위): 아무것도 안 더함
            pass
        elif r < size and c >= size:
            # 2사분면 (오른쪽 위)
            count += size * size
            c -= size
        elif r >= size and c < size:
            # 3사분면 (왼쪽 아래)
            count += 2 * size * size
            r -= size
        else:
            # 4사분면 (오른쪽 아래)
            count += 3 * size * size
            r -= size
            c -= size
    return count


N, r, c = map(int, input().split())
print(z_order(N, r, c))

후기

항상 느끼지만, 재귀 문제는 문제 지문을 통해 수학 개념을 어떻게 끌어내는지가 가장 관건인 것 같다.
이 문제를 해결하는 2가지 방법에 대해 고민할 수 있었는데,

1. 사례를 분석하여 수식을 이끌어내는 과학 실험적인 방법
2. 4등분된 정사각형의 넓이를 더해나가는 과정을 수식으로 작성하는 수학적인 방법

두 방법 모두 의미있는 고민 과정이었던 것 같다.

코드의 작성은 입력된 좌표가 어느 사분면에 해당하는지 판별하는 조건문이 핵심이었다. 이를 위해 배열의 중심을 추출하기 위해 전체 크기의 절반을 좌표로 사용했다.