이런 것, 한 번 쯤은 본적 있지 않은가?

검은 화면, 하얀 색 특수문자들로 돌아가는 3D 도넛을 만든다.
분명 간단한 프로그램 같지만 묘하게 보는 맛이 있다.
이것은 Donut.c이다.
이렇게 ASCII 문자열로 그림을 그리는 것을 ASCII Art라고 한다.

"에이, 그래봤자 콘솔창에 글자 출력하는 건데."

하지만 쉽게 보면 곤란하다.
그래픽에 관련된 만큼, 한 번 파고 들어가보면 심오한 수학의 세계가 펼쳐져 있기 때문.

이 글에서는 그 수학을 한 번 이해해 보려고 한다.

Donut.c

이 콘솔 도넛에 대한 나의 관심은 한 유튜브 동영상에서부터 시작되었다.
그 동영상은 "why you NEED math for programming", 번역하면 "프로그래밍에 수학이 필요한 이유" 라는 영상이다.

이 글의 끝에서 어떻게 도넛이 아스키 코드로 렌더링 되는지를 간략한 수학적 원리로 설명해준다.
그것을 듣고 관심이 생겨 인터넷에 검색해보게 되었다.

놀랍게도, 생각보다 이것에 대한 글이 많이 없었다.
고작 간략한 한국어 소개 글과 복잡한 영어 수학적인 원리를 설명해주는 글 뿐.

처음에는 영어에 복잡한 수학까지 섞여 있어 읽기 꺼려졌지만, 작정하고 읽다보니 읽을 만 했다.

그럼 이제 진짜로 분석을 시작해보자.
여기에 나오는 수학적인 원리는 이 글을 참고했다. (영어 좀 치는 사람은 원문 읽어도 된다)

수학적인 원리

일단, 어떻게 저것을 구현해야 할 지를 생각해 보자.
두 가지가 필요하다.

1. 도넛의 형상을 그리기
2. 도넛의 형상에 밝기를 나타내기

일단 3D 렌더링은 제쳐두고, 일반적인 ASCII Art에서 어떤 방식으로 밝기를 표현하는지를 알아보자.

ASCII Art를 출력할 곳이 터미널인데, 일반적으로 터미널은 바탕이 검정색이고 문자가 흰 색이다.
따라서 한 글자가 차지하는 공간 안에서 픽셀의 밀도가 높으면 밝은 색, 픽셀의 밀도가 낮으면 어두운 색으로 정할 수 있다.
이를 간단한 12 글자로 나타낸 것이 아래의 글자들이다.
.,-~:;=!*#$@
왼 쪽이 가장 어두운 색, 오른 쪽이 가장 밝은 색이다.

자, 이제 3D 1인칭 시점에서 쓰이는 간단한 수학으로 시작해 보자.

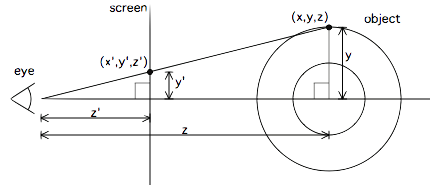
위의 그림은 사람이 스크린 앞에 앉아서 스크린 뒤의 물체를 쳐다보는 그림이다.

3차원의 물체를 2차원에 그리기 위해, 3차원의 각각의 점 (x, y, z)를 시청자의 z’만큼 떨어진 평면에 투영한다.
그러면 그 점은 (x’, y’)이 될 것이다.
3차원 물체의 각각의 점의 좌표를 알고 있는 상황에서 2차원의 어디에 투영해야 할 지를 알아야 하므로 x, y를 가지고 x’, y’을 알아야 한다. (z’은 실수이므로 K1이라고 하자.)

수학 식으로 나타내면 y’ / K1 = y / z
z’을 이항하면 y’ = y * K1 / z

이 식은 x에도 똑같이 적용할 수 있다. (x’ = x * K1 / z)

또한 많은 점들을 투영하면서 x와 y는 같지만 z가 다른 점을 투영해야 할 일이 생길 수도 있으므로, z를 저장하는 zbuffer를 만들 것이다.
이 zbuffer의 기본 값은 z ^ -1 (z의 -1제곱)이 될 것인데, 그 이유는 다음과 같다.

1. z ^ -1 = 0 이면 z는 무한에 가까우므로, 기본값이 0이 되었을 때 배경을 무한대 깊이로 설정해 아무것도 없도록 할 수 있다.
2. x’과 y’을 구할 때 다시 이용할 수 있다. (z ^ -1 = 1 / z, z를 미리 나눠 둠으로서 굳이 z를 두번 나누지 않고 조금 더 효율적으로 연산할 수 있다.)

도넛 (solid of revolution)

자, 그럼 이제 도넛 형상을 어떻게 만들 지를 고민해야 한다.
다행히도, 도넛은 회전체(solid of revolution) 이므로 다음과 같은 원리를 통해 각각의 점을 구할 수 있다.

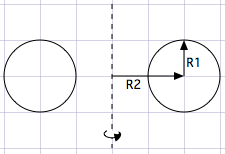
보다시피 (R2, 0, 0) 점을 중심으로 한 R1이 반지름인 원이 있다.
R1을 중심으로 한 원은 0~360도로 돌려줌으로서 그릴 수 있다.
0~360도까지 변하는 변수를 θ(세타)로 두자.

이것을 식으로 나타내면 다음과 같다.
(x, y, z) = (R2, 0, 0) + (R1cosθ, R1sinθ, 0)
이 식으로 원 하나를 구할 수 있다.

이제 이 원을 y축을 따라 돌려보자. 바로 도넛 모양이 나온다는 것을 눈치 챘을 것이다.
이 원을 y축을 따라 회전시키기 위해서는 회전 변환 행렬을 이용해 구할 수 있다.

y축을 따라 돌려야 하므로, 3차원 y축 회전 변환 행렬을 가져와 곱하면 아래와 같은 식이 나온다.

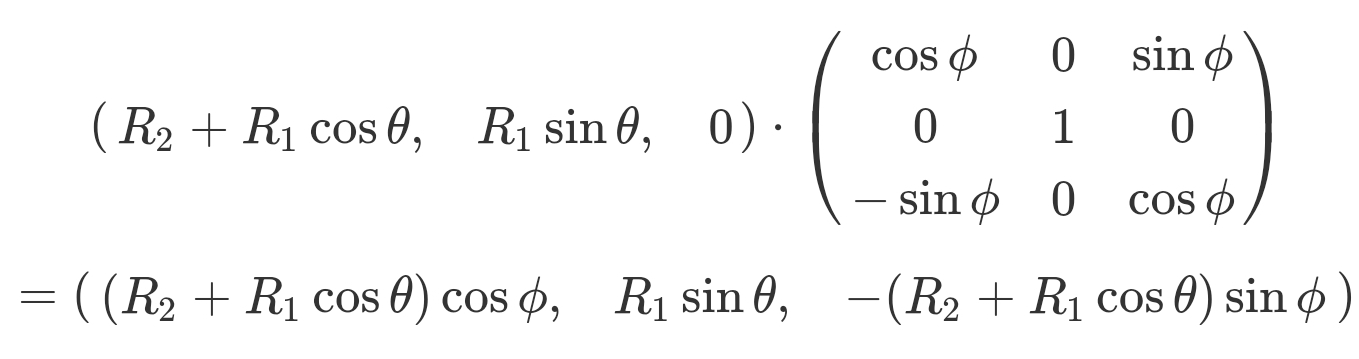
그런데 우리는 이 도넛이 두 개 이상의 축에서 회전하도록 구현하고 싶기 때문에, 2개의 회전 변환 행렬을 더 가져와 곱한다.
또한 가져온 2개의 회전 변환 행렬에서 쓰이는 각도는 A와 B로 칭한다.
식은 다음과 같다.

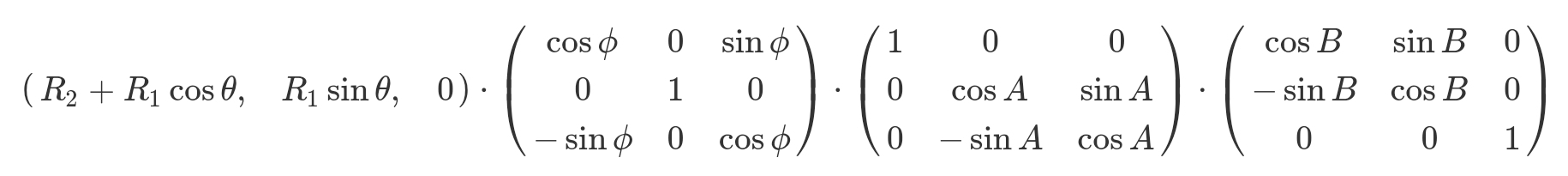
이제 우리는 원점인 (0, 0, 0)을 기준으로 하는, A와 B라는 각에 의해 일정하게 회전하는 도넛의 좌표들을 가지고 있다.

이제 이것을 실제로 화면에 투영하기 위해서는 시청자의 좌표가 (0, 0, 0)이라고 가정하고, 도넛을 시청자의 앞 쪽으로 옮겨야 한다.
도넛을 시청자의 앞쪽으로 옮기기 위해, z에 시청자와 도넛이 떨어진 거리를 더해야 한다.
이 시청자와 도넛이 떨어진 거리를 K2라고 하자.

이제 실제 (x’, y’)을 구하기 위한 식은 다음과 같다.

(x’, y’) = (K1 x / (K2 + z), K1 y / (K2 + z))

그리고, (x, y, z)를 구하기 위한 식은 다음과 같다.

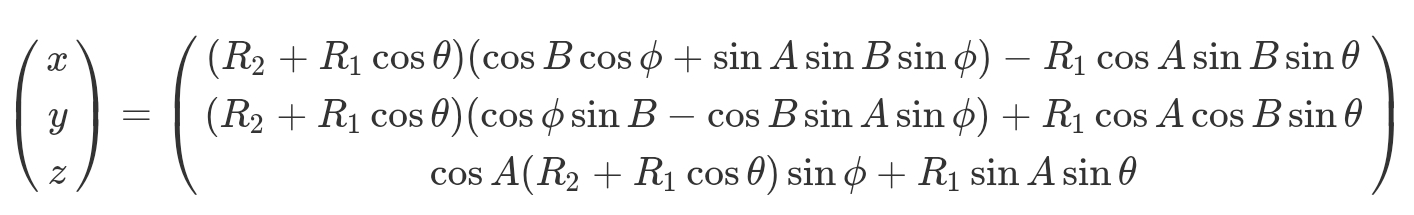
최대한 최적화 하기 위해, 프로그래밍 단계에서는 행렬 곱셈을 쓰지 않고 위의 계산 식을 사용할 것이며, 또한 (R2 + R1 * cosθ)와 같은 값을 미리 계산해 식에서 재사용하도록 할 것이다.

밝기

이제 어느 곳에 점을 둬야 할 지는 알았지만, 그 각각의 점에 대한 밝기는 아직 모른다.
광도를 계산하기 위해 필요한 수학적 개념은 법선surface normal이다.

이 법선을 구하고 나면, 이 법선과 빛의 방향 간의 내적을 구할 수 있게 되고, 이 내적은 법선과 빛의 방향 간의 각도를 코사인한 값을 포함하고 있다.

벡터 a와 벡터 b에 대한 내적은 a · b = |a||b|cosθ 이므로
만약 이 내적이 0보다 크다면 cosθ > 0 이므로 그 위치의 점이 빛을 바라보고 있으므로 밝고, 0보다 작다면 그 위치의 점이 빛을 바라보고 있지 않아 어두울 것이다.
즉, 내적이 크면 클 수록 더 많은 빛이 점에 떨어진다.

그런데, 생각해보면 이 법선 벡터는 구하기 매우 쉽다.
왜냐하면 (0, 0, 0)에서 최종적인 (x, y, z)까지의 벡터가 (x, y, z) 점의 법선벡터가 되기 때문이다.
따라서, 위의 회전 변환 행렬과 같이 식을 다시 쓸 수 있다.

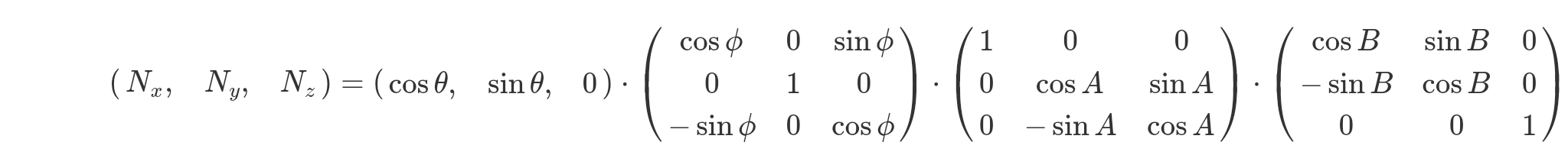
이 식에서 다른 점은, 시작점이 (cosθ, sinθ, 0)이라는 것이다.
이는 정확한 x, y, z의 값이 아니라, 각 θ에 대한 코사인과 사인으로 방향만을 나타낸 것이다. (크기는 정확하지 않다.)

자, 그렇다면 이제 빛의 방향을 정해야 한다.
시청자의 뒤쪽 위에서 빛을 비추는 것은 어떨까?
그렇다면 빛의 벡터는 (0, 1, -1)이 된다.
이제 아까의 법선 벡터와 이 빛의 벡터의 내적을 구해보자.

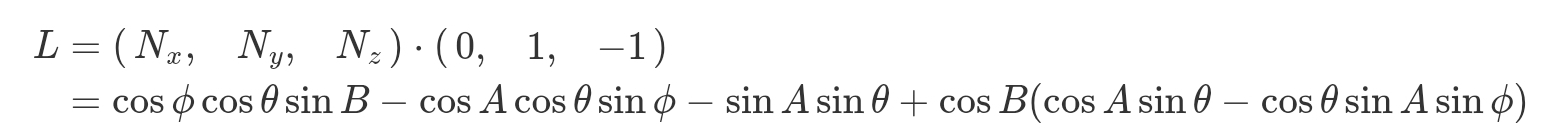
자, 이제 마지막으로 해야 할 일은 상수를 정하는 것이다.
정하지 않은 상수에는 도넛의 전체 크기와 링의 두께를 정할 R1, R2가 있고, 또 크기를 나타낼 K1, 관찰자와 도넛 사이의 거리를 나타낼 K2가 있다.

먼저 R1과 R2는 각각 1과 2로 정하고, K2는 5로 정했다.
K1의 경우 크기를 나타내는데, 화면의 크기(한 화면에 나타낼 수 있는 ASCII 글자의 수)에 따라 달라지므로 다음과 같이 식을 짤 수 있다.

먼저 도넛이 나타낼 수 있는 최대 가로(최대 x 좌표)는 R1+R2이고, z는 0이다.
그 점이 화면의 가로 3/8 지점 쯤에 나타나도록 하려면,

screen_width * 3/8 = K1 * (R1+R2) / (K2 + 0)
screen_width * K2 * 3 / (8 * (R1+R2)) = K1

위와 같이 나타낼 수 있다.

따라서 파이썬과 numpy로 나타낸 최종 코드는 다음과 같다.

import numpy as np
screen_size = 40
theta_spacing = 0.07
phi_spacing = 0.02
illumination = np.fromiter(".,-~:;=!*#$@", dtype="<U1") 
A = 1
B = 1
R1 = 1
R2 = 2
K2 = 5
K1 = screen_size * K2 * 3 / (8 * (R1 + R2)) 
def render_frame(A: float, B: float) -> np.ndarray: 
    cos_A = np.cos(A) 
    sin_A = np.sin(A) 
    cos_B = np.cos(B) 
    sin_B = np.sin(B) 
    
    output = np.full((screen_size, screen_size), " ")
    zbuffer = np.zeros((screen_size, screen_size))
    
    cos_phi = np.cos(phi := np.arange(0, 2 * np.pi, phi_spacing)) # (315,) 
    sin_phi = np.sin(phi)
    cos_theta = np.cos(theta := np.arange(0, 2 * np.pi, theta_spacing)) # (90,)
    sin_theta = np.sin(theta)
    
    circle_x = R2 + R1 * cos_theta
    circle_y = R1 * sin_theta
    
    x = (np.outer(cos_B * cos_phi + sin_A * sin_B * sin_phi, circle_x) - circle_y * cos_A * sin_B).T
    y = (np.outer(sin_B * cos_phi - sin_A * cos_B * sin_phi, circle_x) + circle_y * cos_A * cos_B).T
    z = ((K2 + cos_A * np.outer(sin_phi, circle_x)) + circle_y * sin_A).T
    ooz = np.reciprocal(z) 
    xp = (screen_size / 2 + K1 * ooz * x).astype(int)
    yp = (screen_size / 2 - K1 * ooz * y).astype(int)
    L1 = (((np.outer(cos_phi, cos_theta) * sin_B) - cos_A * np.outer(sin_phi, cos_theta)) - sin_A * sin_theta)
    L2 = cos_B * (cos_A * sin_theta - np.outer(sin_phi, cos_theta * sin_A))
    L = np.around(((L1 + L2) * 8)).astype(int).T
    mask_L = L >= 0 
    chars = illumination[L] 
    for i in range(90): 
        mask = mask_L[i] & (ooz[i] > zbuffer[xp[i], yp[i]]) 
        zbuffer[xp[i], yp[i]] = np.where(mask, ooz[i], zbuffer[xp[i], yp[i]])     
        output[xp[i], yp[i]] = np.where(mask, chars[i], output[xp[i], yp[i]]) 
        return output 
def pprint(array: np.ndarray) -> None:
    print(*[" ".join(row) for row in array], sep="\n") 
    
if __name__ == "__main__": 
    for _ in range(screen_size * screen_size): 
        A += theta_spacing 
        B += phi_spacing 
        print("\x1b[H") 
        pprint(render_frame(A, B))