수포자를 위한 삼각함수와 역삼각함수 (feat. 게임서버)

(그 수포자가 바로...나!😂😂😂)

삼각함수의 정의

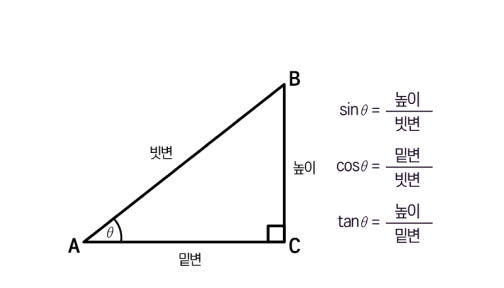
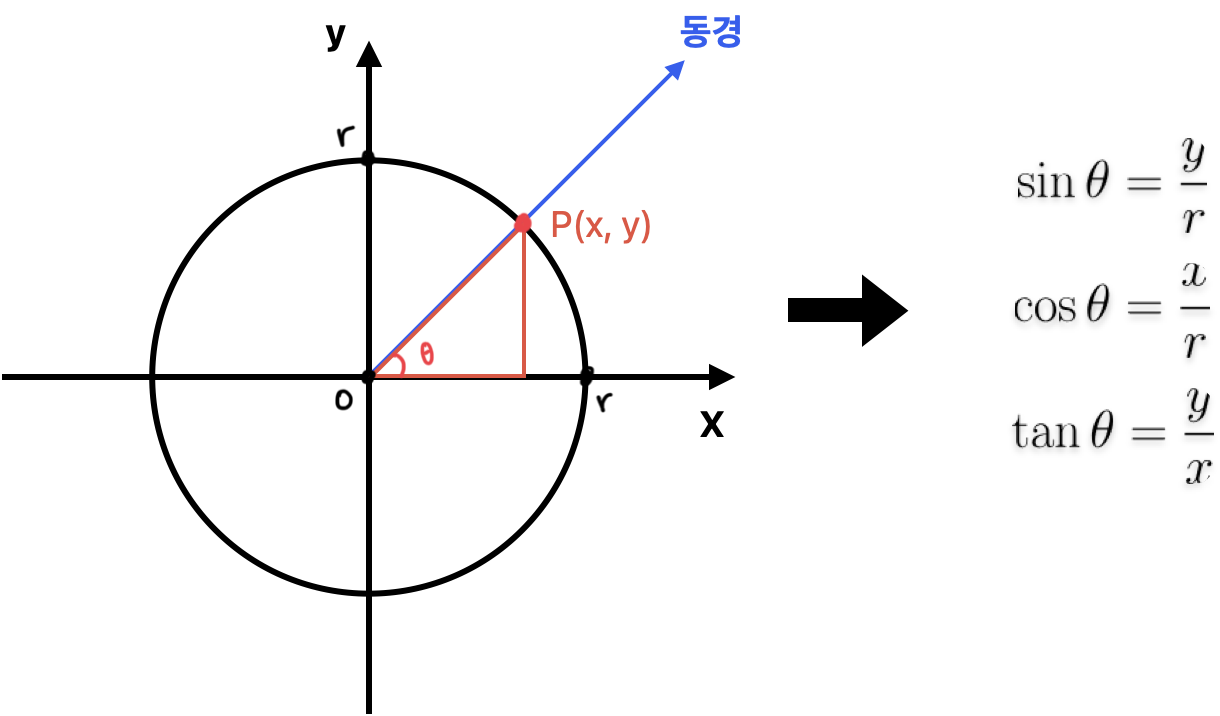
삼각함수란 직각삼각형에서 각도(θ)를 입력받아,
해당 각도의 삼각비(두 변의 길이의 비율)를 반환하는 함수이다.

출력값은 비율이므로 단위가 없는 값이다.

• 주요 삼각함수 : 사인(sin), 코사인(cos), 탄젠트(tan)
• 각도 표현 : 보통 각도는 세타(θ)로 표현하며, 호도법으로 각도를 표현할 때는 일반 함수의 변수처럼 x를 사용한다.

(1) 삼각비란?

삼각비란 삼각형의 세변의 길이 중 두 변의 길이의 비율을 말한다.

멀리 있는 건물의 높이를 알고 싶을 때, 건물까지의 거리와 올려다 보는 각도만 알면, 삼각비를 통해 높이를 구할 수 있다.

✅ 삼각비를 활용한 예제

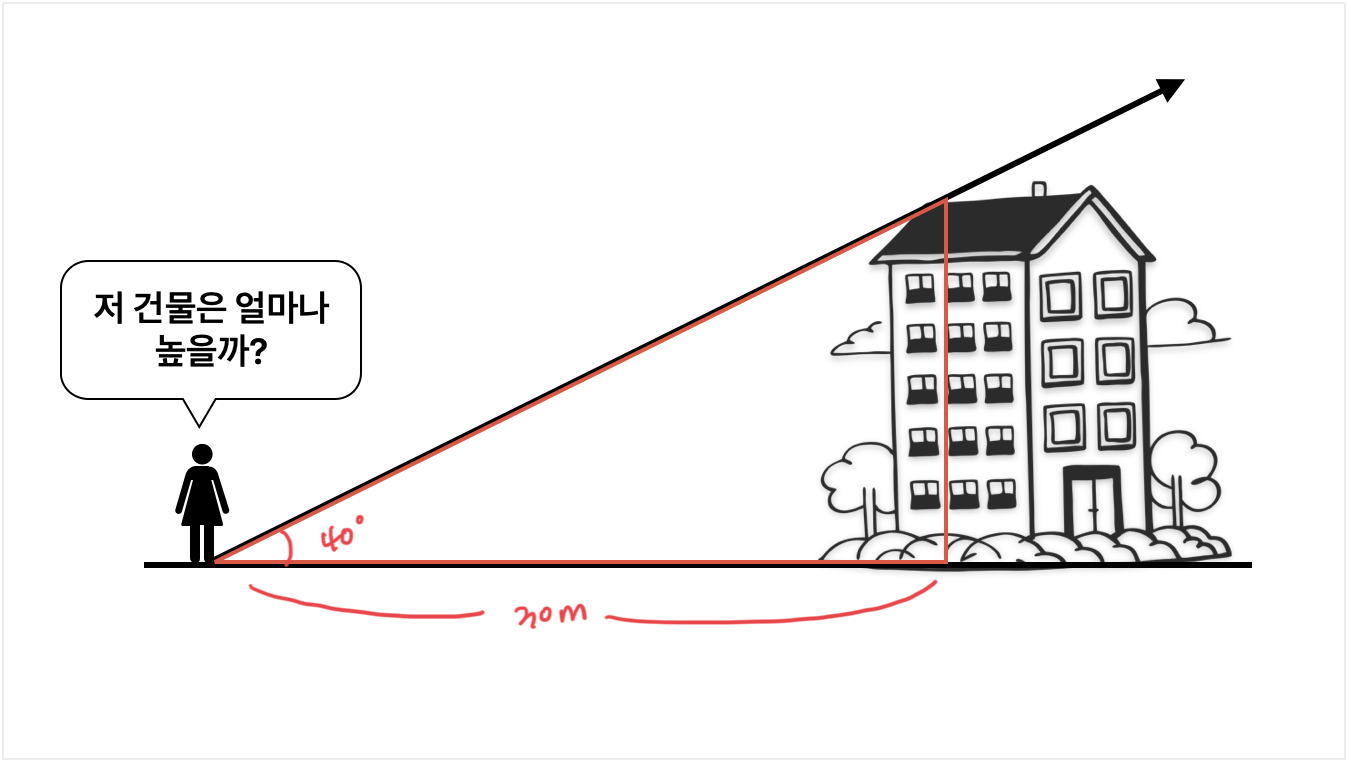
• 건물까지의 거리 (밑변) : 30m
• 올려다보는 각도($\theta$) : 40도
• 건물의 높이는?!

  📝 풀이

  $\tan (\theta) = \frac{\text{높이}}{\text{밑변}}$
  여기서 우리는 세타값과 밑변 값을 알고 있다.

  $\tan (40°) = \frac{\text{높이}}{\text{밑변(30m)}}$
  $\tan (40°) = 0.8391 = \frac{\text{높이}}{\text{밑변(30m)}}$
  $\text{높이} = 0.8391 * 30 = 25.17m$

❓길이의 비율인데, 각도가 무슨 상관인가요?

$\sin\theta = \frac{높이}{빗변의 길이}$

수식을 보면, sin = 이 아닌 sinθ =로 표시되어 있다.

• 각도는 어떤 변이 높이고 어떤 변이 밑변인지 결정하는 기준이 되기에 필수적이다.
• 직각삼각형의 빗변은 언제나 직각인 각과 마주보는 변이므로 절대적이지만, 나머지는 상대적이기 때문이다.
• 기준이 되는 각과 마주보는 변이 높이가 되고, 나머지 하나가 밑변이 된다.

💡 게임 서버에서는 어떻게 활용될까?

• 캐릭터가 보스몬스터를 향해 스킬을 쏠 때, 캐릭터와 보스몬스터 사이의 각도를 계산하는 데 삼각함수를 사용한다.
• 원거리 공격이 실제로 보스몬스터에 맞았는지 계산할 때도 삼각함수가 사용된다.

(2) 호도법이란?

우리가 흔히 쓰는 90°, 180° 대신, 파이(π)를 사용하는 방법이다.

마치 시계에서 1시, 2시처럼 원을 등분해서 사용하는 것으로,
시계의 12시가 0이라면, 3시는 π/2, 6시는 π, 9시는 3π/2라고 생각하면 된다!

• 각도를 라디안으로 변환하려면?
  - radian = (각도 × π) / 180
• 라디안을 각도로 변환하려면?
  - 각도 = radian × 180 / π

TMI
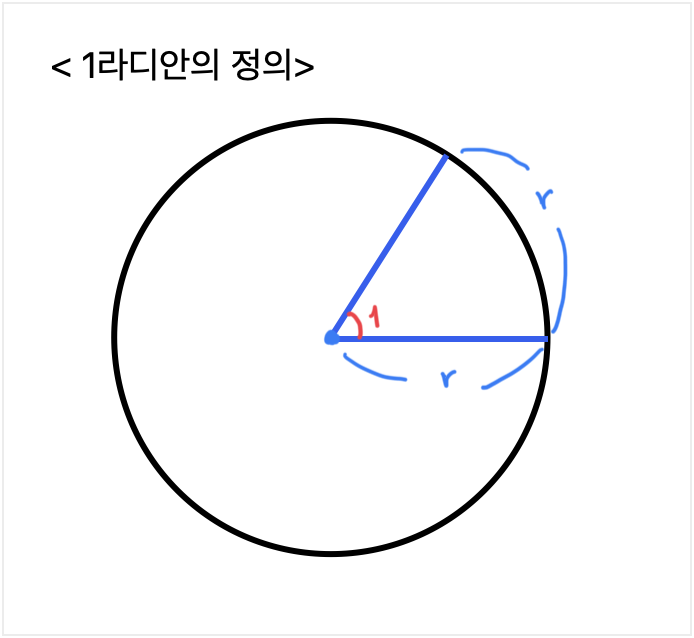
호도법은 각도의 단위를 없애기 위해 수학자들이 창안한 방법으로, 반지름과 호의 길이가 같은 부채꼴이 중심각을 1라디안이라고 정의한다. (라디안은 단위가 아니라 하나의 기호로 생각하면 됨)

💡 게임 서버에서는 어떻게 활용될까?

• 게임에서 캐릭터가 회전할 때 호도법을 사용한다.
• 예를 들어, 캐릭터가 오른쪽으로 90도 회전하면 π/2만큼 회전한다고 계산한다!

(3) 동경이란?

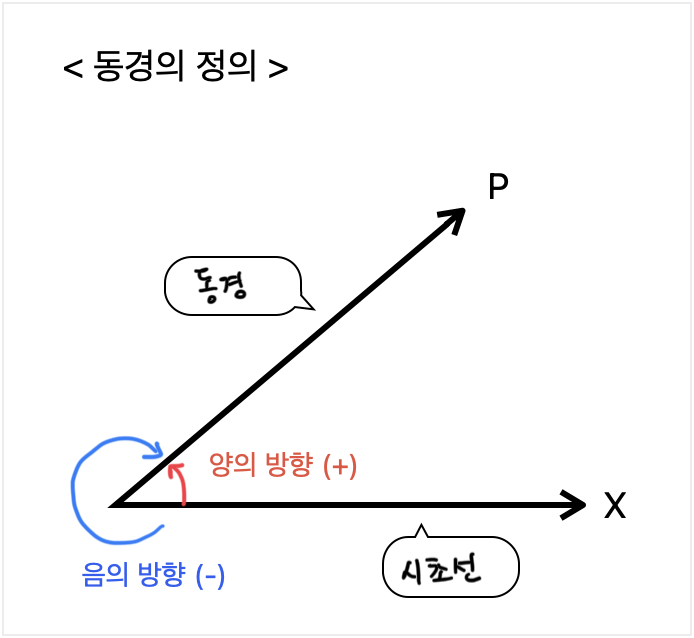
동경은 기본적으로 반직선이다.

쉽게 말해서, 시계의 12시 방향을 기준으로 얼마나 회전했는지를 나타내는 선이라고 볼 수 있다.

역삼각함수의 정의

역삼각함수는 삼각비 값을 입력받아 그에 해당하는 각도를 출력하는 함수이다.
예를 들어, arctan은 주어진 삼각비에 대해 라디안 단위로 각도를 반환한다.

쉽게 설명하면:

• 삼각함수 : "각도를 넣으면 -> 비율이 나옴"
• 역삼각함수 : "비율을 넣으면 -> 각도가 나옴"

• 주요 역삼각함수 : 아크사인(arcsin 또는 sin⁻¹), 아크코사인(arccos 또는 cos⁻¹), 아크탄젠트(arctan 또는 tan⁻¹)
• 정의역과 치역 : 역삼각함수는 정의역의 범위를 제한하여 역함수를 나타낸다.

💡 게임 서버에서는 어떻게 활용될까?

• 마우스로 클릭한 위치(x, y 좌표)가 있을 때, arctan(y/x)로 각도를 구할 수 있다.
• 캐릭터가 어떤 방향을 바라봐야 할지 계산할 때 매우 유용하다.
• 예를 들어 보스몬스터를 자동으로 추적할 때, 몬스터의 위치와 캐릭터의 위치로 각도를 계산한다.

역삼각함수의 특징

1. 입력값 범위가 정해져 있다.
   • arcsin과 arccos는 -1에서 1 사이의 값만 넣을 수 있다.
   • arctan은 어떤 값이든 넣을 수 있다.
2. 결과값(각도)의 범위가 정해져 있다.
   • arcsin: -90도에서 90도 사이
   • arccos: 0도에서 180도 사이
   • arctan: -90도에서 90도 사이

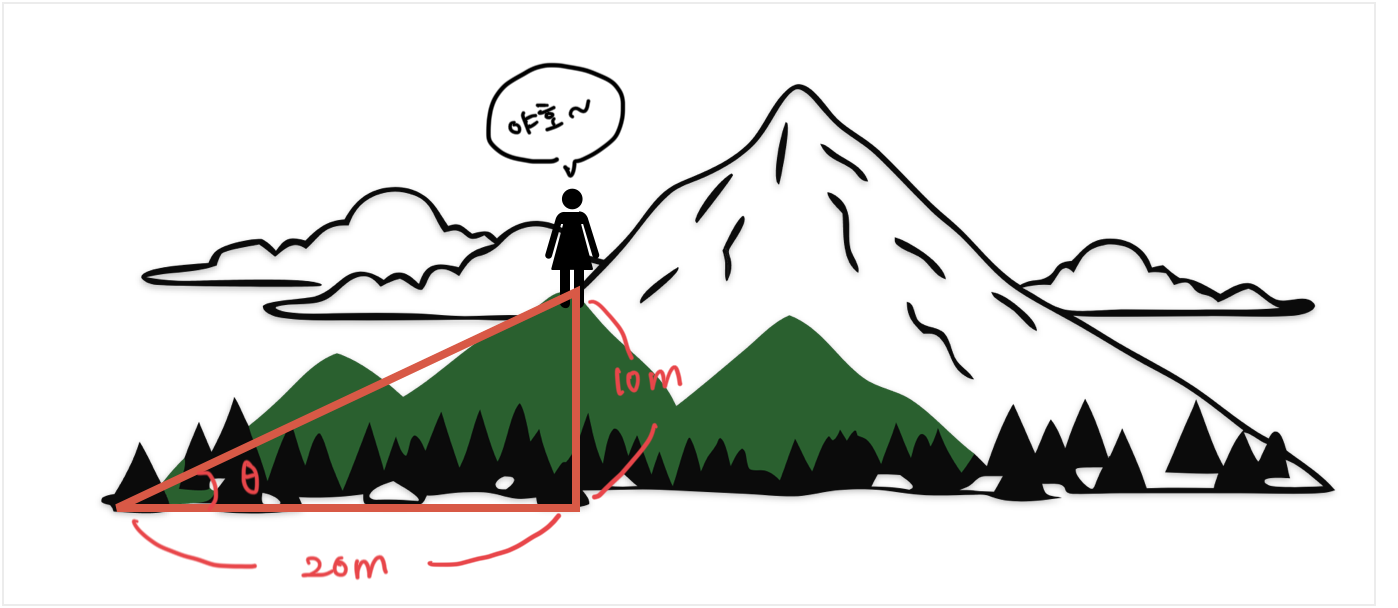
💡 실생활 예시!
등산할 때 경사도를 측정하는 상황을 생각해봅시다.

(문제) 10m 올라갔는데 앞으로 20m 갔다면?
$tan(\theta) = \frac{10}{20} = 0.5$
$\theta = \text{arctan}(0.5) = 0.4636 \text{ rad}$
$0.4636 \times \frac{180}{\pi}$
$\theta \approx 0.4636 \times 57.2958 = 26.57^\circ$
(정답) "길의 경사도는 대략 26.6도구나!!!"

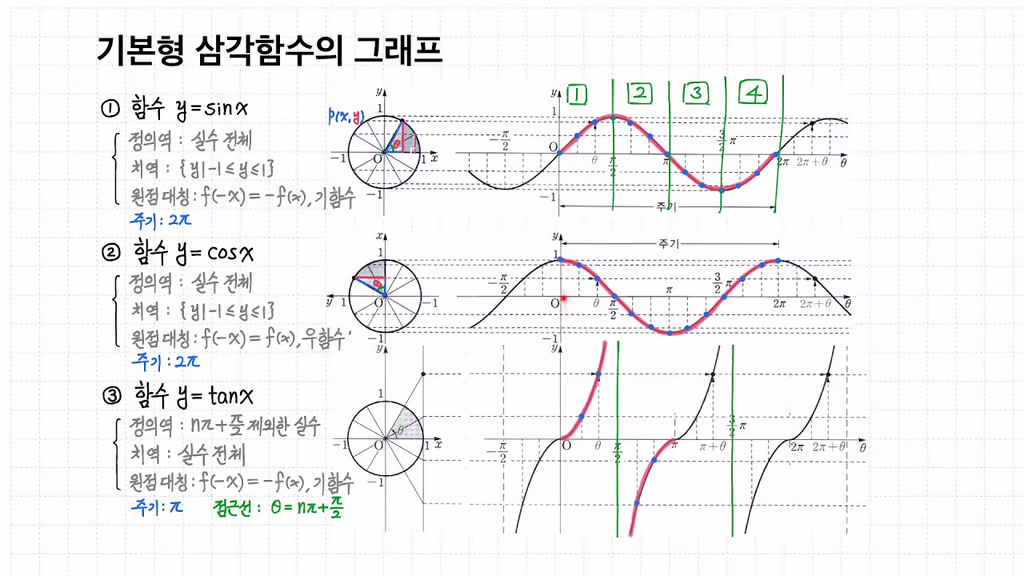
삼각함수의 그래프

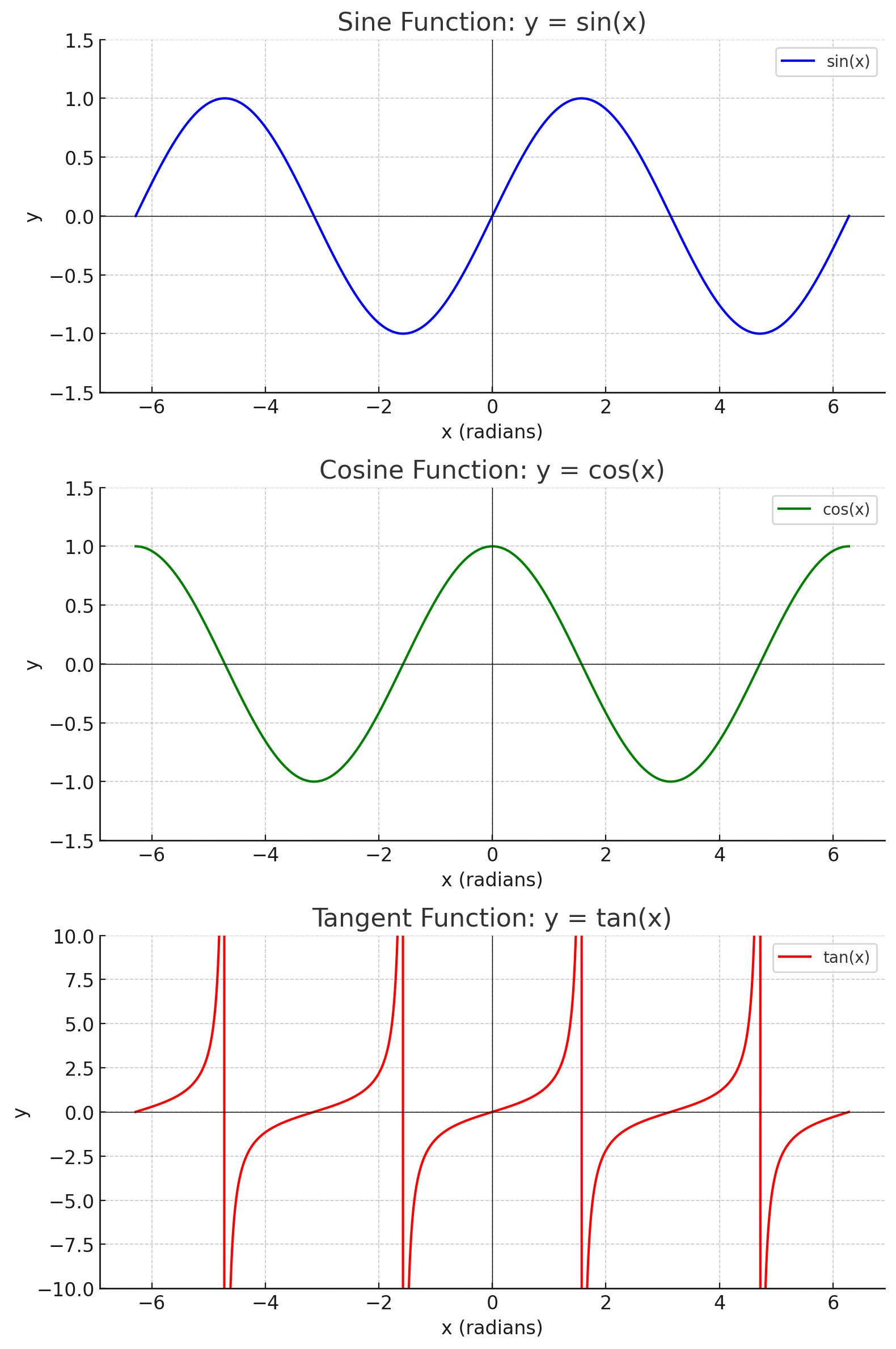
삼각함수의 그래프는 반복되는 패턴을 가지고 있다.

• sin 함수 그래프 : 주기적이며, y축을 중심으로 대칭이다.
• cos 함수 그래프 : 사인 함수와 유사하지만, x축을 기준으로 이동한 형태이다.
• tan 함수 그래프 : 주기적이며, 점근선을 가진다.

삼각함수의 그래프는 일정한 주기를 가진다!

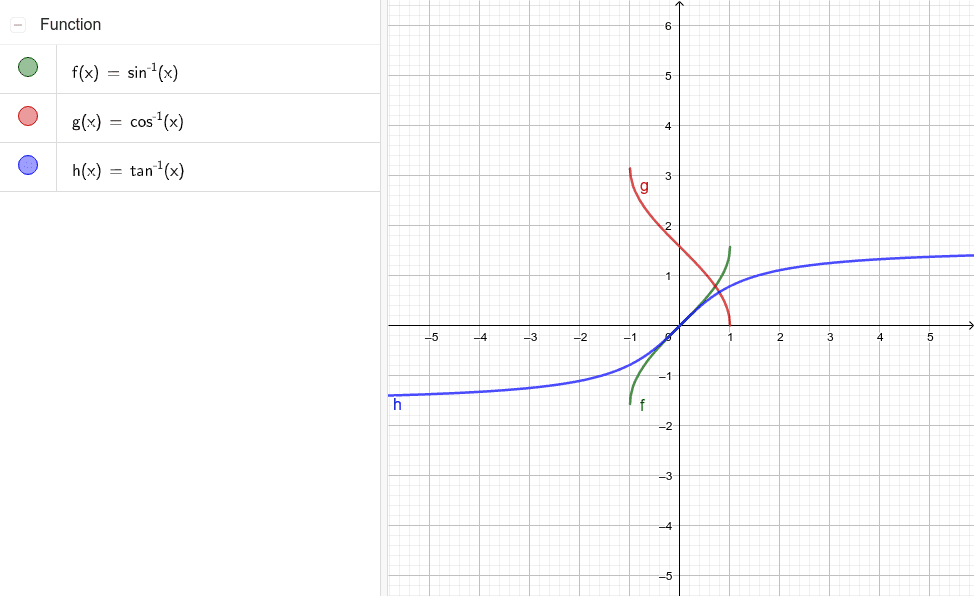
역삼각함수의 그래프

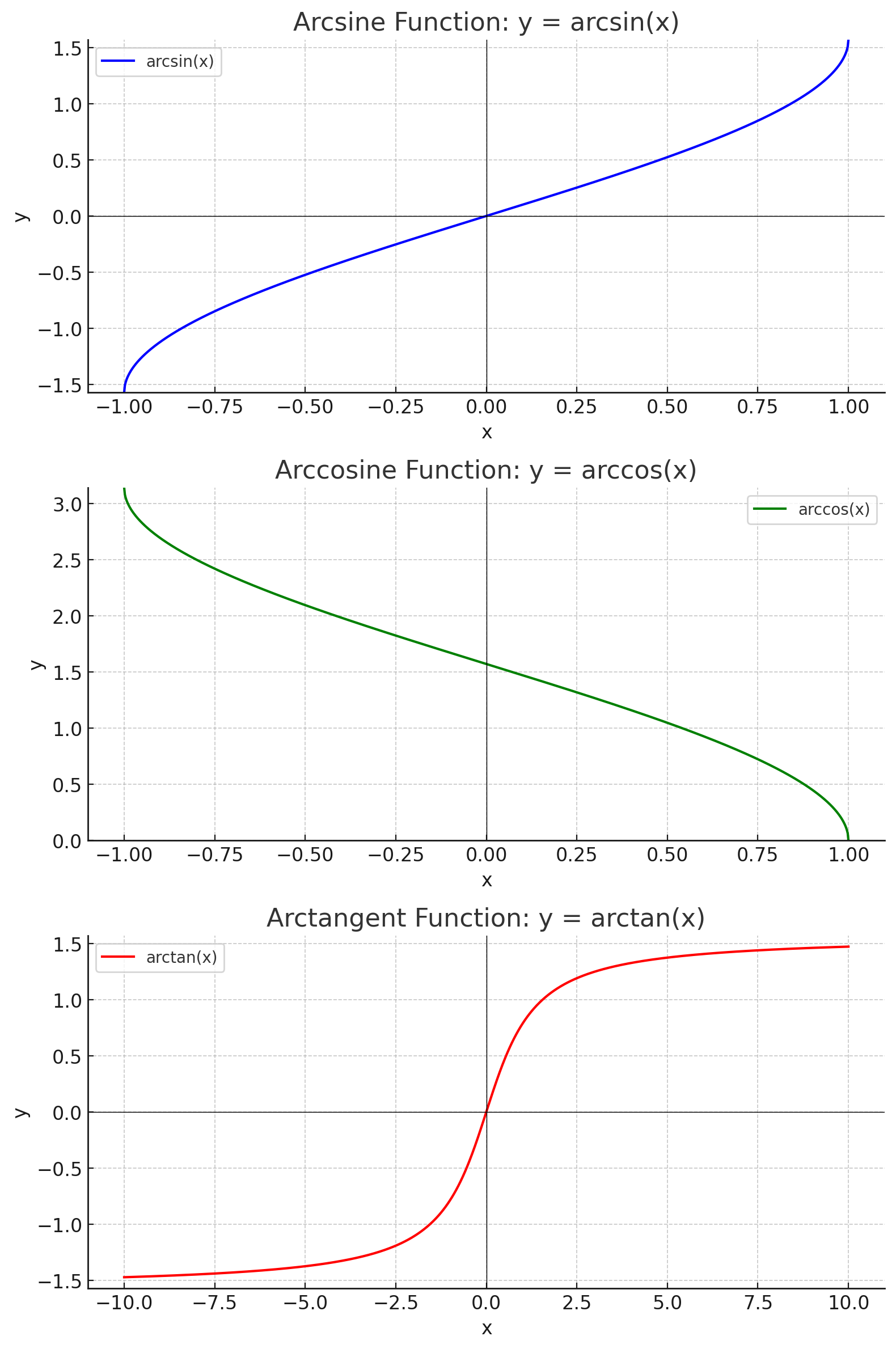
역삼각함수의 그래프는 특정 범위에서만 정의되며, arcsin과 arccos은 점근선을 가지지 않는다. arctan는 정의역이 실수 전체이고, 결과는 점근선 (-π/2, π/2)에 수렴한다.

• 아크사인 함수 그래프: 정의역은 [-1,1], 치역은 [-π/2, π/2]이다.
• 아크코사인 함수 그래프: 정의역은 [-1,1], 치역은 [0, π]이다.
• 아크탄젠트 함수 그래프: 정의역은 실수 전체, 치역은 (-π/2, π/2)이다.

게임 서버에서 삼각함수와 역삼각함수의 활용 예시

1. 삼각함수 활용 예시: 캐릭터 이동 궤적 계산

삼각함수는 캐릭터가 특정 방향으로 이동할 때 좌표를 계산하는데 유용하다.

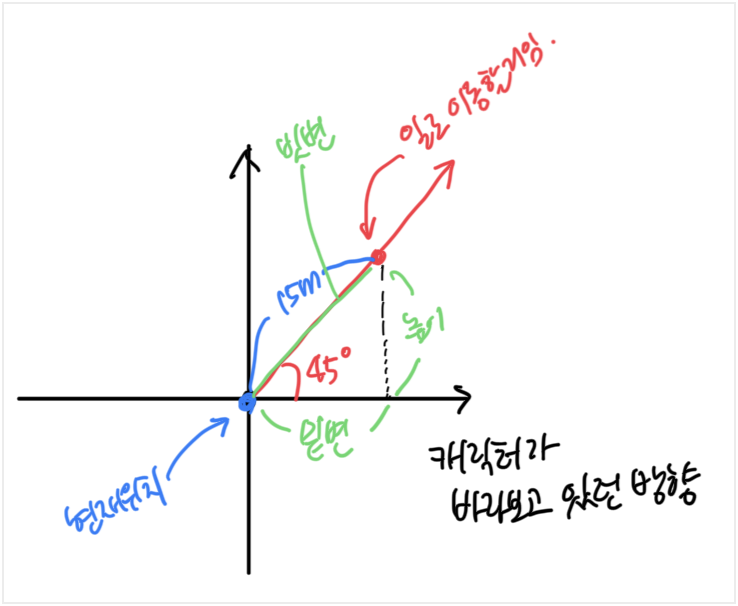
✅ 캐릭터가 $\theta(45^\circ)$ 방향으로 15m 이동하려고 할 때, 이동될 좌표 값은???

• 초기 좌표: $(x₀, y₀) = (100, 100)$
• 이동 거리: 15m
• 이동 방향: $\theta = 45^\circ$
  

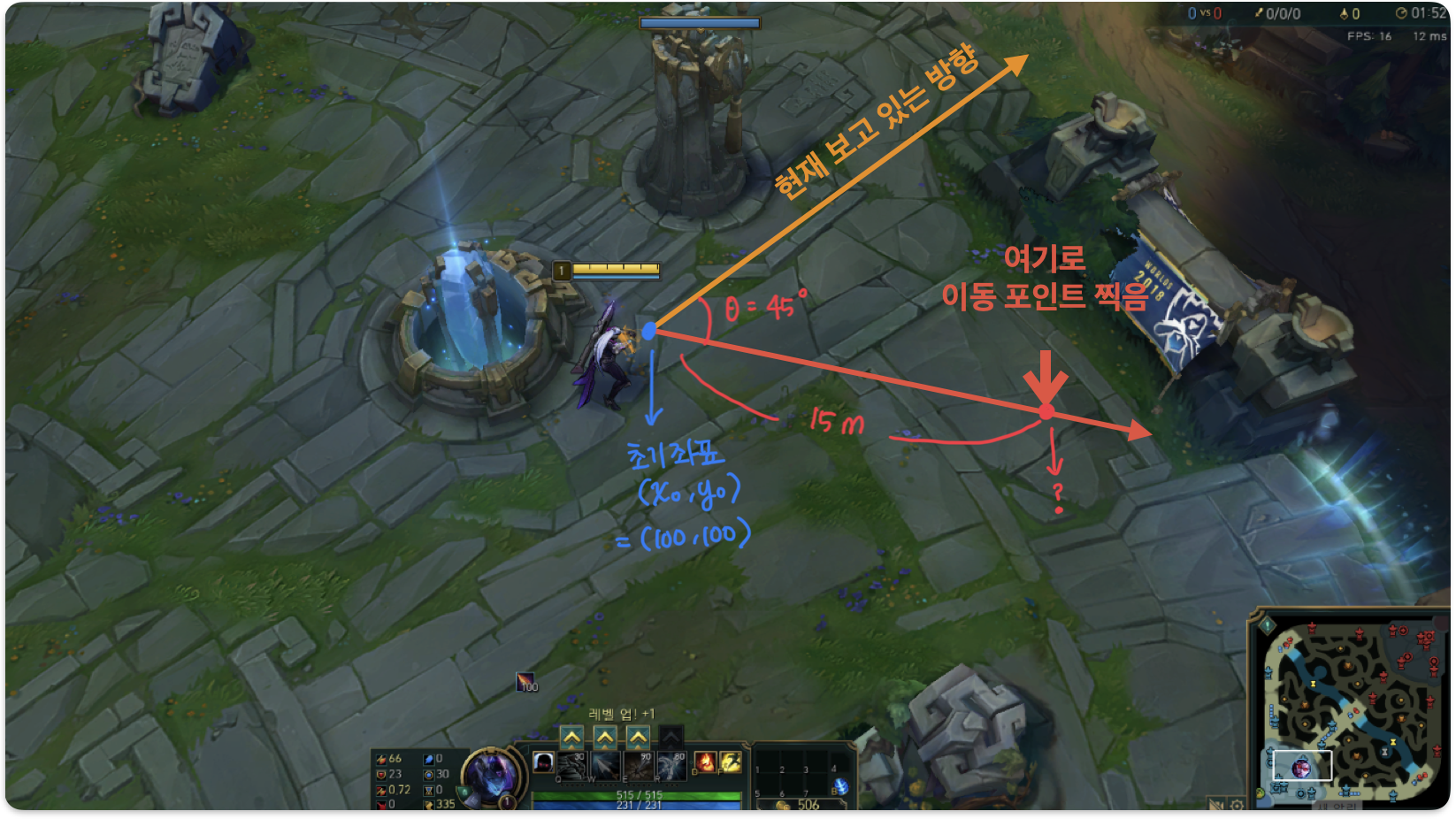
📝 풀이

1. 이동 방향 (각도)을 radian 으로 변환하기
   • 왜냐! 컴퓨터나 프로그래밍 언어에서 삼각함수 계산(예: sin, cos)은 radian 단위를 사용하기 때문!
   • $\theta_{\text{radian}} = 45^\circ \times \frac{\pi}{180} = \frac{\pi}{4} \approx 0.7854 \text{ rad}$
   • 45도는 대략 0.7854 radian이 나온다.
2. x축 방향으로 얼마나 이동했는지 계산하기 (dx)
   • $cos\theta = \frac{\text{밑변}}{\text{빗변}}$ 을 활용!
   • $dx = \text{이동 거리(빗변)} \times \cos(\text{radian})$
   • $dx = 15 \times \cos(0.7854)$
   • $dx = 15 \times 0.7071 \approx 10.61$
   • 따라서!!! 대략 10.61 만큼 x축으로 이동한 것!
3. y축 방향으로 얼마나 이동했는지 계산하기 (dy)
   • $sin\theta = \frac{\text{높이}}{\text{빗변}}$ 을 활용!
   • $dy = \text{이동 거리(빗변)} \times \sin(\text{radian})$
   • $dy = 15 \times \sin(0.7854)$
   • $dy = 15 \times 0.7071 \approx 10.61$
   • 따라서!!! 대략 10.61 만큼 y축으로 이동한 것!
4. 새로운 좌표 계산하기
   • 캐릭터가 이동한 후의 좌표를 구하려면, 원래 좌표에서 x, y축으로 이동한 거리만큼 더하면 된다.
   • $x_1 = 100 + 10.61 = 110.61$
   • $y_1 = 100 + 10.61 = 110.61$
   • 이동 후 좌표: $(x_1, y_1) = (110.61, 110.61)$

2. 역삼각함수 활용 예시: 적 추적 각도 계산

역삼각함수는 캐릭터가 적을 추적할 때 두 점 사이의 각도를 계산하는데 사용할 수 있다.

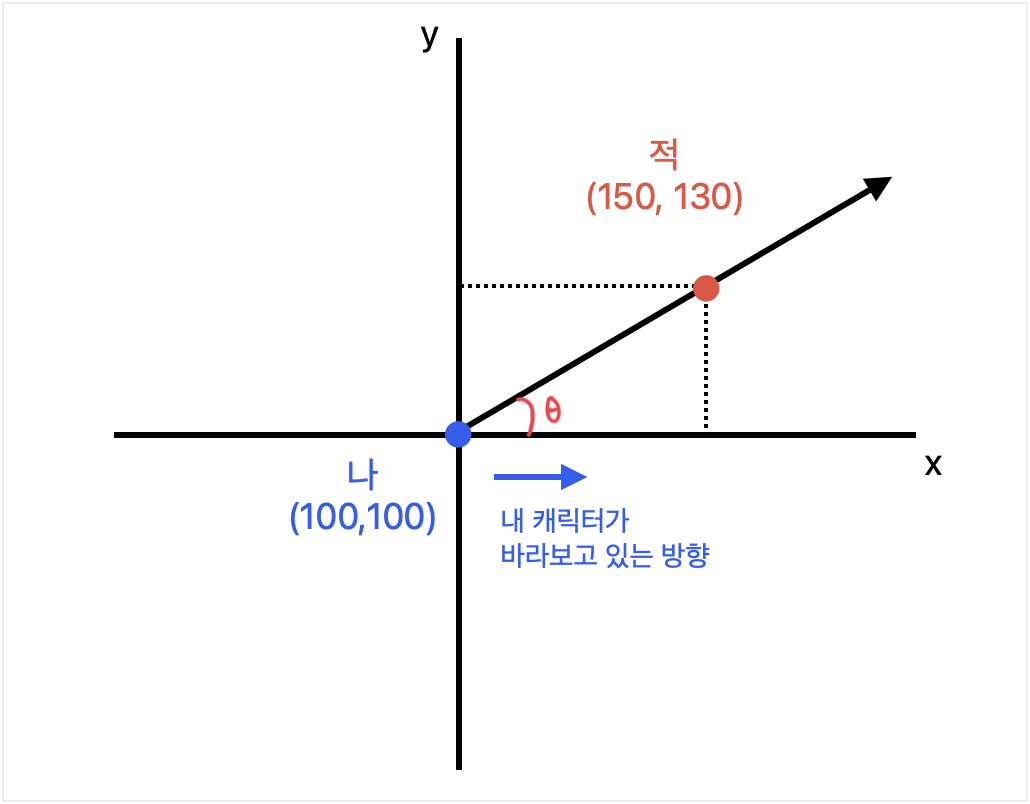
✅ 내 캐릭터가 적 캐릭터에게 가기 위해서는 몇 도를 회전해야 할까?

• 내 캐릭터 좌표: $(x_2, y_2) = (150, 130)$
• 적 캐릭터 좌표: $(x_1, y_1) = (100, 100)$

📝 풀이

각도를 계산하려면 삼각형의 변의 비율이 필요하다.
우리는 이미 밑변과 높이를 알고 있으니 $tan\theta = \frac{높이}{밑변}$ 을 통해 비율을 구할 수 있다.

1. 두 점의 상대적인 x와 y 거리 계산하기
   • $dx = x_2 - x_1 = 150 - 100 = 50$
   • $dy = y_2 - y_1 = 130 - 100 = 30$
2. arctan으로 각도 구하기
   • $\theta = \arctan\left(\frac{30}{50}\right) = \arctan(0.6)$
   • 대략 $\theta \approx 0.5404 radian$ 이 나온다.
3. radian을 degree(도)로 변환하기
   • 변환 공식: $\text{degree} = \text{radian} \times \frac{180}{\pi}$
   • $\text{degree} = 0.5404 \times \frac{180}{3.1416} \approx 30.96^\circ$
   • 결과~~~ 약 31도 이다~!!! ===> 반시계 방향으로 31도를 회전하면 된다~!