개린이가 쓴 글이므로 오류가 있을 수 있음을 미리 알려드립니다 🐹 (꾸벅)
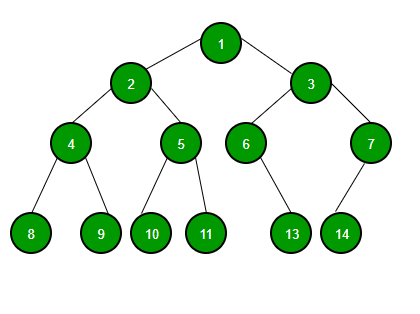
🌲 트리란?
- 트리는 그래프의 단순한 형태이다.
- 트리는 순환하는 것이 없다.
- 부모가 없는 노드를 루트노드라고 하고, 자식이 없는 노드를 잎노드라고 한다.
swift 코드
public class TreeNode<T> {
public var value: T // 노드 안의 값
public weak var parent: TreeNode? // 이 노드의 부모
public var children = [TreeNode<T>]() // 이 노드의 자식들
public init(value: T) {
self.value = value
}
public func addChild(_ node: TreeNode<T>) { // 자식노드 추가
children.append(node) // 자식 배열에 append
node.parent = self // 그 노드의 부모는 나다 !!!
}
}아래의 extension을 통해 tree의 구조를 print 해볼 수 있습니다.
extension TreeNode: CustomStringConvertible {
public var description: String {
var s = "\(value)"
if !children.isEmpty {
s += " {" + children.map { $0.description }.joined(separator: ", ") + "}"
}
return s
}
}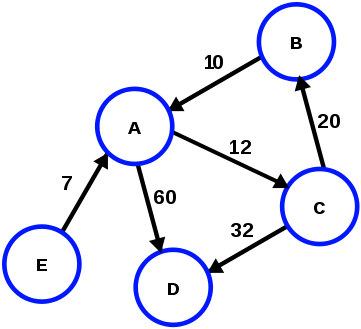
🔄 그래프
- 노드와 그 노드를 연결하는 선을 모아놓은 자료구조
- 방향 / 무방향 그래프 둘 다 존재
- 노드(node) = 정점(vertex)
간선(edge) = 링크 / 브랜치 - 그래프를 그린 후 BFS / DFS 같은 알고리즘을 사용하여 문제를 푼다.
<노드 코드>
public struct Vertex<T>: Equatable where T: Equatable, T: Hashable {
public var data: T
public let index: Int
}<간선 코드>
public struct Edge<T>: Equatable where T: Equatable, T: Hashable {
public let from: Vertex<T>
public let to: Vertex<T>
public let weight: Double?
}이제 그래프 코드를 보자 !!!
그래프를 구현하는 방식에는 2가지가 있다
- 인접 리스트로 구현
- 인접 행렬로 구현
두 개는 각각 장단점이 존재한다.
아래의 표를 통해 확인해보자
여기에서 V는 노드의 개수 / E는 간선의 개수이다.
| 연산 | 인접 리스트 | 인접 행렬 |
|---|---|---|
| 공간 복잡도 | ||
| 노드 추가 | ||
| 간선 추가 | ||
| 연결 확인 |
인접리스트 장점
- 메모리를 덜 차지함. (딱 노드 + 간선 개수만큼만 차지)
- 전체 노드를 다 확인해야 할 때 의 시간복잡도
인접리스트 단점
- 노드와 노드가 연결되어있는지 확인할 때 의 시간이 걸린다.
인접 행렬의 장점
- 노드와 노드가 연결되어있는지 확인할 때 의 시간복잡도
- 구현이 좀 더 간편함
인접 행렬의 단점
- 전체 노드를 다 확인해야 할 때 의 시간복잡도
-> 간선에 비해 노드의 개수가 훨씬 많다면 매우 좋지 않음
1. 인접 리스트로 구현하기
인접 리스트는 그래프의 관계를 벡터 배열로 나타내는 방식
private class EdgeList<T> where T: Equatable, T: Hashable {
var vertex: Vertex<T>
var edges: [Edge<T>]? = nil
init(vertex: Vertex<T>) {
self.vertex = vertex
}
func addEdge(_ edge: Edge<T>) {
edges?.append(edge)
}
}
open override func createVertex(_ data: T) -> Vertex<T> {
// check if the vertex already exists
let matchingVertices = vertices.filter() { vertex in
return vertex.data == data
}
if matchingVertices.count > 0 {
return matchingVertices.last!
}
// if the vertex doesn't exist, create a new one
let vertex = Vertex(data: data, index: adjacencyList.count)
adjacencyList.append(EdgeList(vertex: vertex))
return vertex
}2. 인접 행렬로 구현하기
인접 행렬은 그래프의 연결 관계를 이차원 배열로 나타내는 방법
private class EdgeList<T> where T: Equatable, T: Hashable {
var vertex: Vertex<T>
var edges: [Edge<T>]? = nil
init(vertex: Vertex<T>) {
self.vertex = vertex
}
func addEdge(_ edge: Edge<T>) {
edges?.append(edge)
}
}
open override func createVertex(_ data: T) -> Vertex<T> {
// check if the vertex already exists
let matchingVertices = vertices.filter() { vertex in
return vertex.data == data
}
if matchingVertices.count > 0 {
return matchingVertices.last!
}
// if the vertex doesn't exist, create a new one
let vertex = Vertex(data: data, index: adjacencyMatrix.count)
// Expand each existing row to the right one column.
for i in 0 ..< adjacencyMatrix.count {
adjacencyMatrix[i].append(nil)
}
// Add one new row at the bottom.
let newRow = [Double?](repeating: nil, count: adjacencyMatrix.count + 1)
adjacencyMatrix.append(newRow)
_vertices.append(vertex)
return vertex
}
+ 수정예정 ....


트리도 무향일 수 있답니다!
참고로 시간 복잡도 쓰실 때,
$기호로 감싸주시면 수식 형태로 바뀌어서 좋아요!