Heap
일반적으로 제가 알고있는 힙의 구조는 우선순위 Queue로 알고 있었습니다.
Heap은 완전 이진트리로 구성되어있고, 다음과 같은 규칙을 따릅니다.
- 부모가 자식보다 항상 큰(또는 작은) 값을 가지고 있는 구조
장점
- 일반적인 배열은 우선순위 큐를 표현할 때 삭제와 삽입을 표현할 때 O(1) ~ O(n) 의 시간복잡도를 가집니다.
- 하지만 Heap 자료구조는 Push와 Pop이 동일하게 O(logN)의 시간이 걸립니다.
( 노드의 높이만큼의 시간이 소요 )
구현(Max_Heap)
Heap = [0] * 20
Heap_size = 0
def heap_push(num):
global Heap_size
Heap_size += 1
# 우선 가장 마지막 노드에 값을 집어 넣는다.
Heap[Heap_size] = num
# 마지막 자식 노드부터 해당 부모노드와 값을 비교하는데
c_node = Heap_size
p_node = Heap_size//2
# 자식노드가 최상위 노드(1)거나
while c_node != 1:
# 부모노드가 더 클때까지 노드 값을 교환한다.
if Heap[c_node] <= Heap[p_node]:
break
Heap[c_node], Heap[p_node] = Heap[p_node], Heap[c_node]
c_node = p_node
p_node = c_node // 2
def heap_pop():
global Heap_size
tmp = Heap[1]
Heap[1] = Heap[Heap_size]
Heap_size -= 1
p = 1
# 자식노드 두개 중 더 큰 값을 자식 노드 번호로 쓴다.
c = p * 2
while c <= Heap_size:
if c < Heap_size and Heap[c + 1] > Heap[c]:
c += 1
# 자식 노드보다 부모 노드가 크면
if Heap[c] <= Heap[p]:
break
# 자식 노드가 부모노드보다 크면 교환
Heap[p], Heap[c] = Heap[c], Heap[p]
p = c
c = p * 2
return tmp
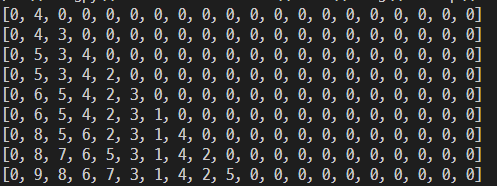
arr = [4, 3, 5, 2, 6, 1, 8, 7, 9]
for num in arr:
heap_push(num)
print(Heap)
while Heap_size:
print(heap_pop())
- Heap에 넣어진 모습은 다음과 같습니다.