
현대 블록암호의 구성 요소
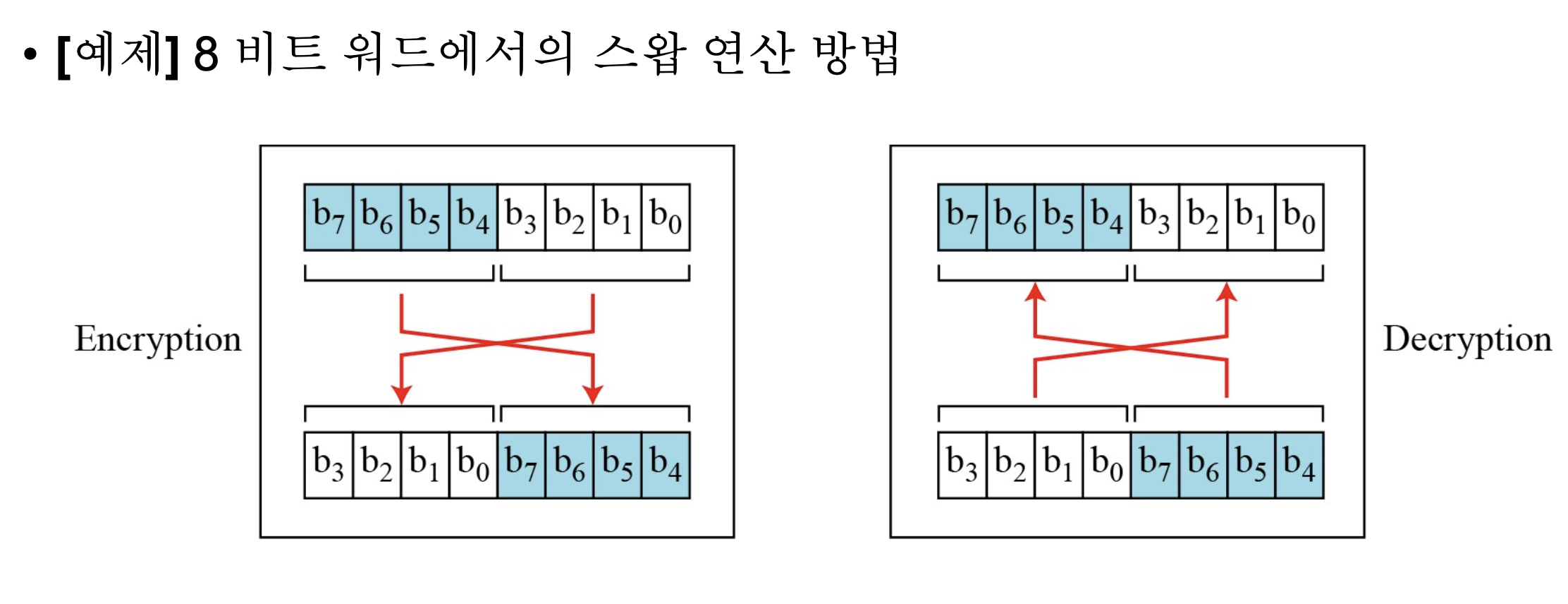
Swap
- k = n/2인 순환 이동 연산의 특수한 경우
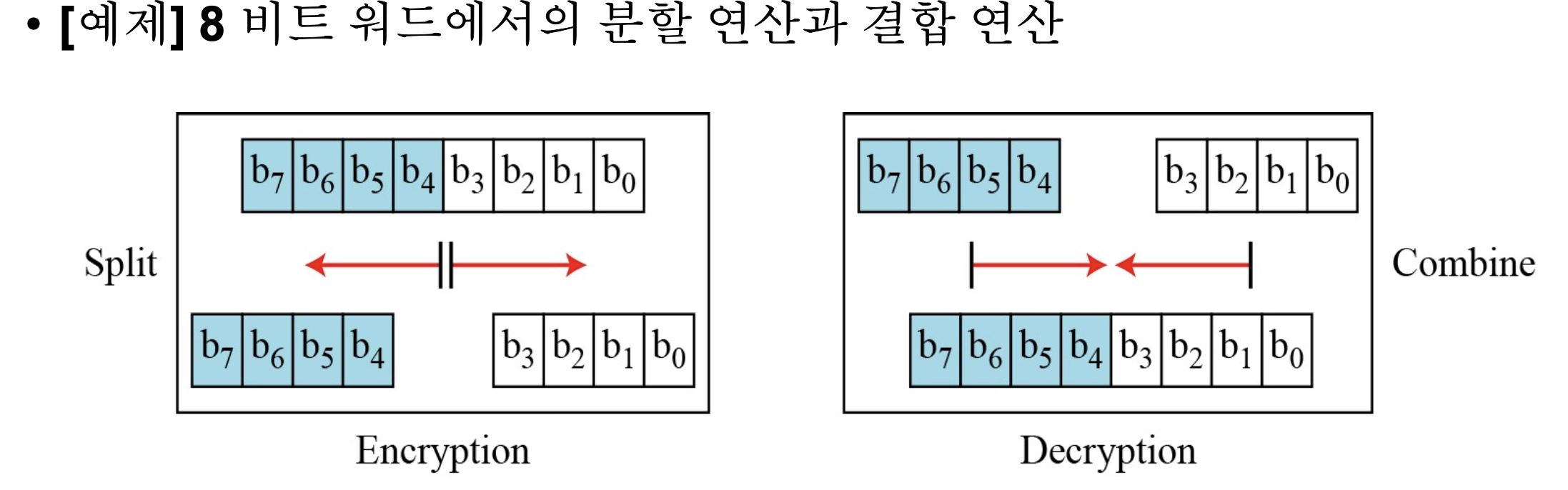
분할과 결합
- n비트 워드를 n/2 비트의 두 워드로 분할하거나 n/2비트의 두 워드를 하나의 n비트로 결합하는 연산
함성 암호
- Shannon에 의해 소개된 개념
- 대치, 치환 그리고 기타의 구성요소들을 결합한 복합적인 암호
- 설계된 블록 암호가 혼돈과 확산의 성질을 갖도록 함
혼돈(Confusion)과 확산(Diffusion)
혼돈
- 암호문과 키의 관계를 숨김
- 암호문을 이용하여 키를 찾고자 하는 공격을 어렵게 하기 위해 키의 단일 비트가 변하면 암호문의 거의 모든 비트들이 변하게 함
키가 조금만 달라져도 키에 의해 생성된 암호문은 완전히 달라지느 게 좋음
확산
- 암호문과 평문 사이의 관계를 숨김
- 통계 테스트를 사용해 암호문에 대한 평문을 찾는 공격을 어렵게 함
- 암호문의 각각의 비트나 문자가 평문의 모든 비트나 특정 비트에 의해 종속적으로 결정되도록 함
- 예를 들면, 평문의 단일 비트가 바뀐다면, 암호문에 있는 특정 비트 또는 모든 비트가 바뀌게 구성함
혼돈: 암호문에서 키를 알아내기 어렵게 하는 성질
확산: 암호문에서 원본 메시지를 알아내기 어렵게 하는 성질
라운드(Rounds)
- 혼돈과 확산은 S-박스와 P-박스 그리고 기타 구성 요소들을 결합하는 합성 암호를 반복적으로 사용해 구현됨
- 이때, 반복적으로 사용되는 합성 암호를 라운드라 함
- 각 라운드에서는
- 키로부터 키 스케줄 또는 키 생성 알고리즘을 통해 생성된 서로 다른 라운드키(서브키(를 사용함
- 이때, 각 라운드에서 생성되는 값을 중간 상태 값(middle text)이라 함
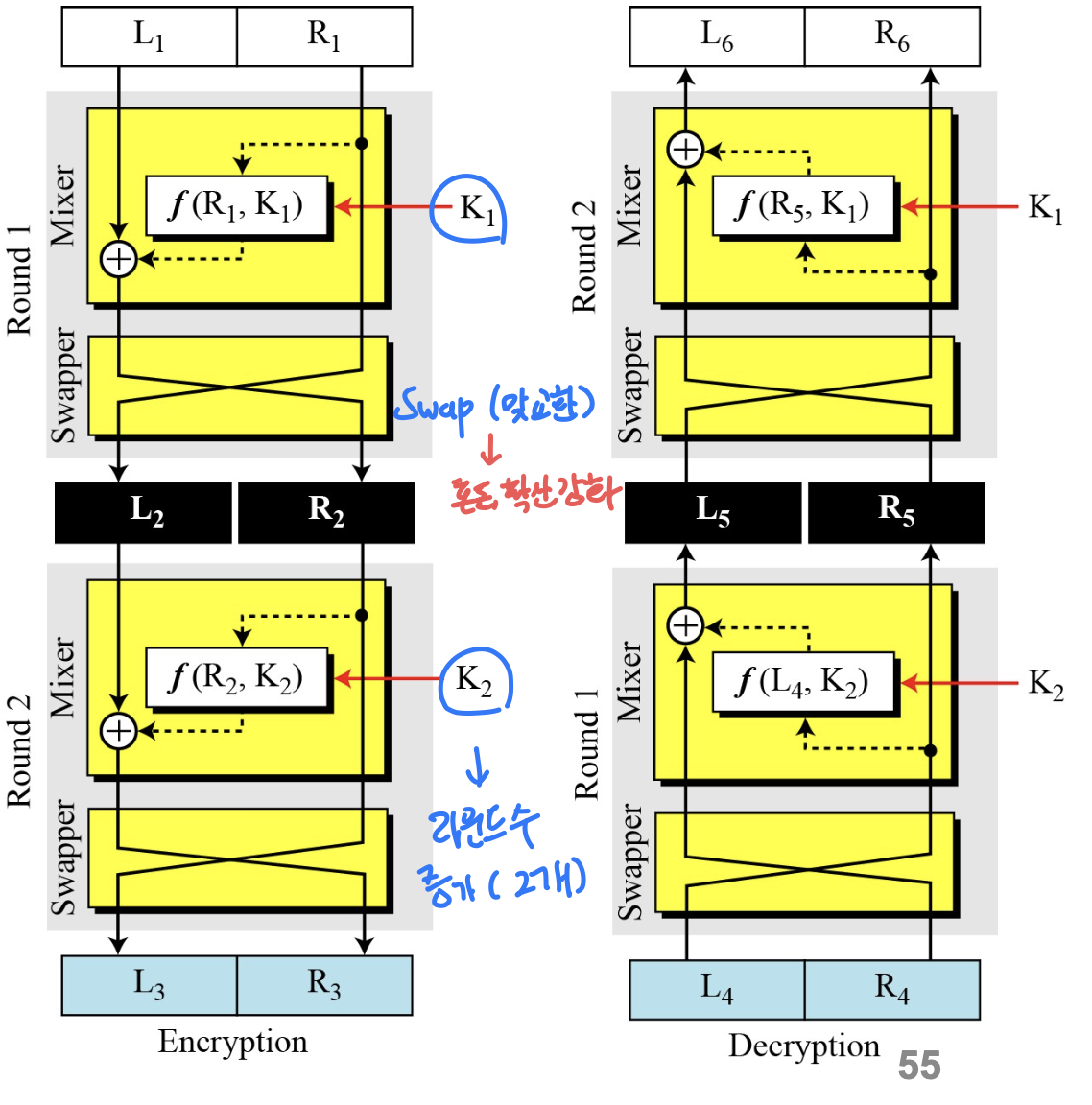
- 두 라운드로 구성된 함성 암호 다이어그램

현대 암호시스템의 구성 방법
- 실제 암호시스템에서는 혼돈과 확산의 효과를 극대화하기 위해 더욱 큰 데이터 블록과 더 많은 S-Box 그리고 더 많은 라운드를 사용함
- 암호문을 더욱 난수처럼(= 유사 난수) 생성되게 함
- 암호문과 평문 사이의 관계를 더욱 알아내기 힘들게 함 (-> 확산)
- 라운드 수의 증가는 라운드 키의 개수를 증가시킴으로써 암호문과 키의 관계를 유추하기 어렵게 함 (-> 혼돈)
라운드 개수 == 라운드 키의 개수
두 종류의 합성 암호
- 현태 블록 암호는 합성 암호임
- Feistel 암호: 역함수가 존재하는 구성요소와 역함수가 존재하지 않는 구성요소 모두를 사용해 설계
- ex) DES
- Non-Feistel 암호: 역함수가 존재하는 구성요소만을 사용하는 설계
- ex) AES
Feistel 암호
- 아래의 세 가지 타임의 요소로 구성됨
- 자기 자신을 역으로 갖는 것(self-invertible)
- 역함수가 존재하는 것(invertible)
- 역함수가 존재하지 않는 것(noninvertible)
- 역이 존재하지 않은 구성요소들을 서로 결합하고, 암호 알고리즘과 복호 알고리즘에서 동일한 구성요소를 사용함
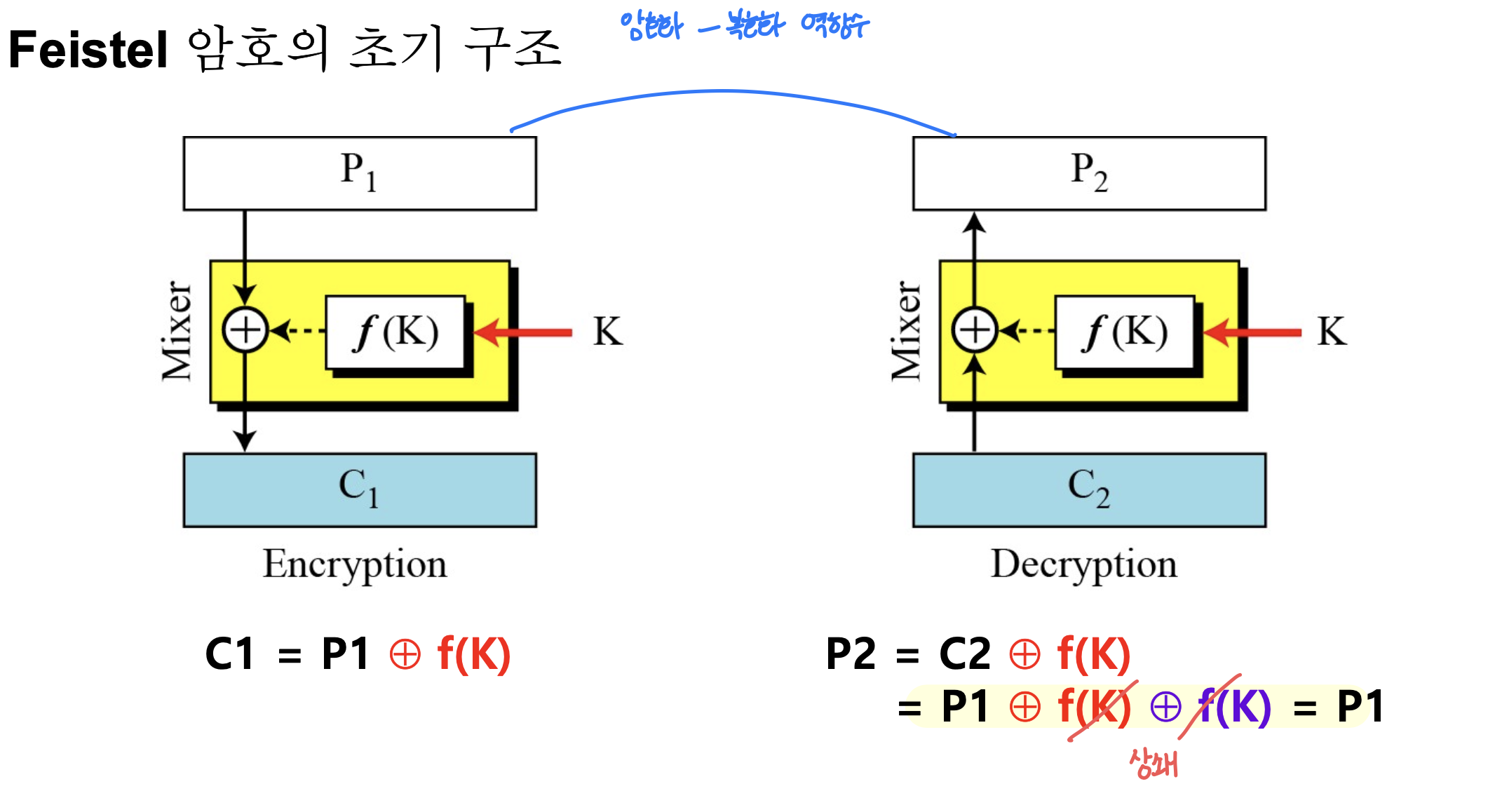
- Feistel 암호의 초기 구조
- 어떻게 역이 존재하지 않는 구성요소로 설계한 암호/복호 알고리즘이 서로 역관계가 될 수 있는가?
- 암호 알고리즘에서 역함수가 존재하지 않는 구성요소의 효과가 복호화 알고리즘에서 상쇄되도록 함

- Feistel 구조에서 믹서는 자기 자신을 역함수로 가짐
- 초기 구조에 대한 향상
- 함수의 입력을 키와 평문으로 복합적으로 구성하기 위해 평문을 두 부분으로 나눔
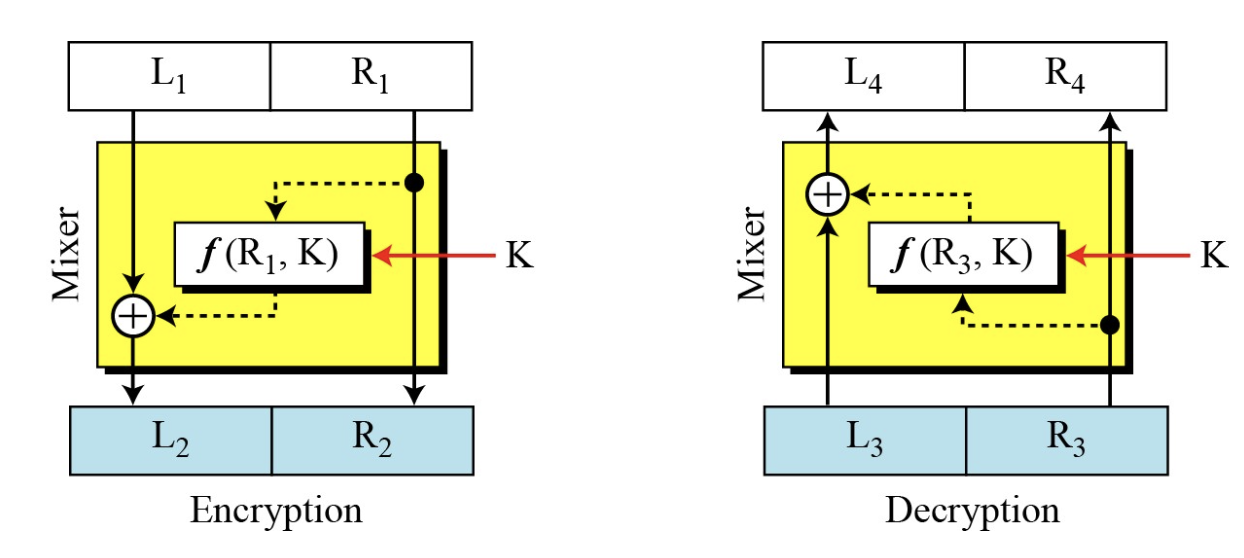
- 함수의 입력을 키와 평문으로 복합적으로 구성하기 위해 평문을 두 부분으로 나눔
- 또한, 암호 알고리즘과 복호 알고리즘은 여전히 서로 역관계
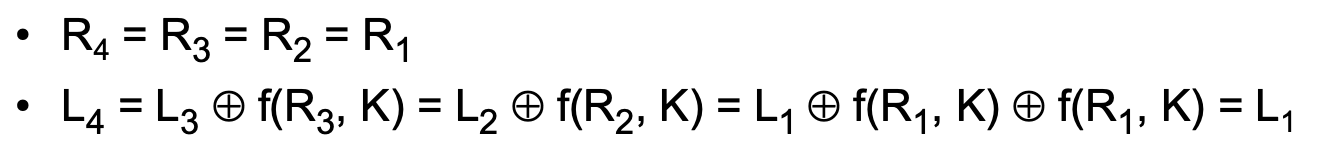
- Feistel 암호
- 이전 버전은 평문의 오른쪽이 암호화되지 않음
- 그러나 Feistel 최종 구조에서는 스와퍼(swapper)를 추가해 각 라운드의 왼쪽과 오른쪽으로 구성
- 총 두 라운드로 구성
- 두 개의 라운드 키 k1, k2를 사용하며, 복호화에서는 역순으로 사용
Non-Feistel 암호
- 역함수가 존재하는 요소만을 사용해 설계
- 암호화를 구성하는 각 요소는 복호화를 구성하는 각 요소에 대응됨
- 주요 특징
- S-Box는 적절하게 동일한 입출력 개수를 가져야 함
- 축소 혹은 확장 P-박스는 역함수가 존재하지 않기 때문에 사용할 수 없음
- 평문이 반씩 분할될 필요 없음
- XOR, 역이 존재하는 2x2 S-Box, 역이 존재하는 단순 P-Box만을 구성요소로 이용
- 복호화에는 라운드 키를 역순으로 이용
블록 암호에 대한 공격 방법
- 블록 암호에는 고전 암호의 공격들이 사용될 수 있음
- 대부분의 공격에 대해 안전
- 특히, 키 사이즈가 매우 크기 때문에 키 전수조사 공격에 안전
- 이에 따라, 블록 암호의 구조에 기반한 새로운 공격 방법이 제한됨
- 차분 분석
- 선형 분석
차분 분석 (Differential Cryptanalysis)
- 선택 평문 공격을 이용
- 공격자는 송신자의 컴퓨터에 어떤 방법으로든 접근해 자신이 선택한 평문에 대한 암호문을 획득함
- 이 공격의 목적은 송신자의 암호화 키를 찾아내는 것
- 분석 순서
- 알고리즘 분석
- 선택 평문 공격의 시작
- 키 값의 추측
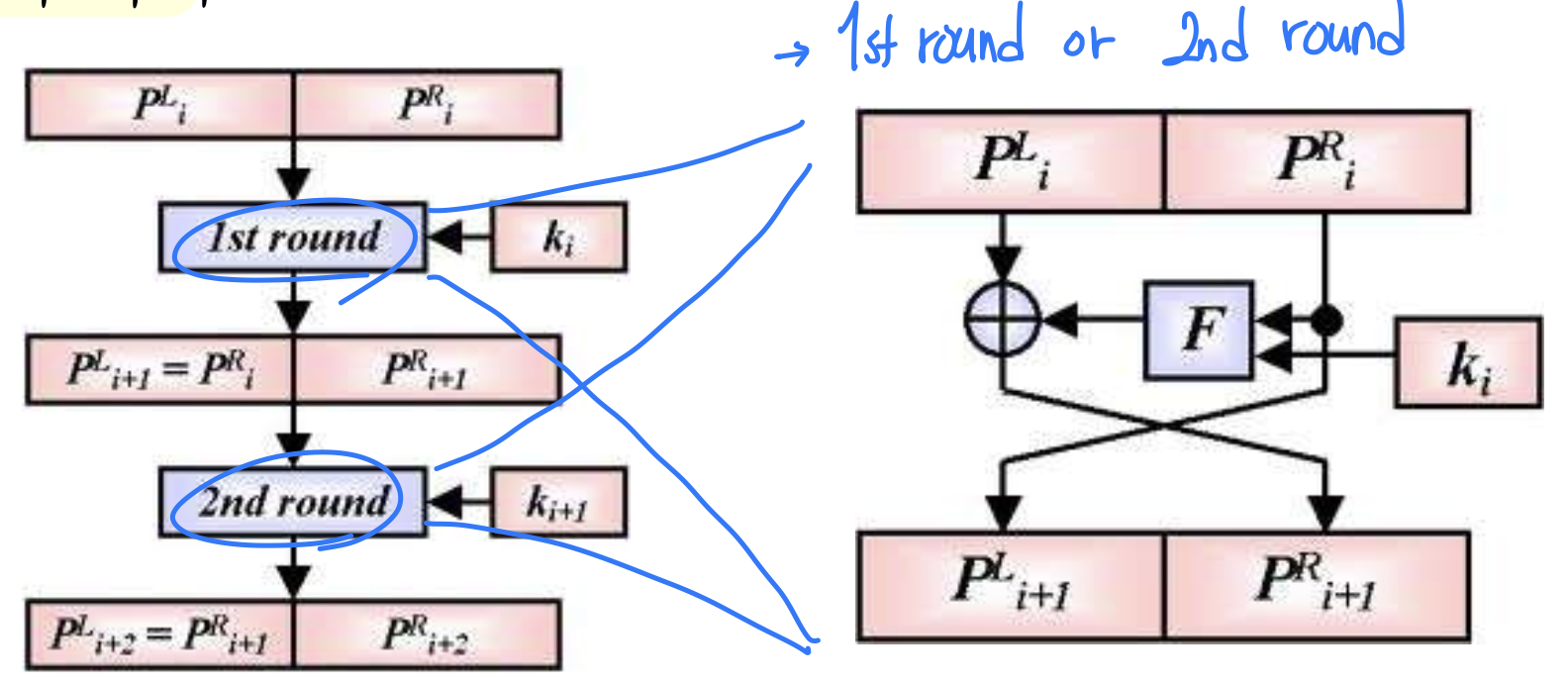
- 차분 분석 알고리즘 분석
- 먼저 암호 알고리즘을 분석해야 함
- 특정 암호는 공격자가 키를 알지 못해도 평문의 차분과 암호문의 차분 사이의 관계를 찾을 수 있는 구조적 취약점을 가짐
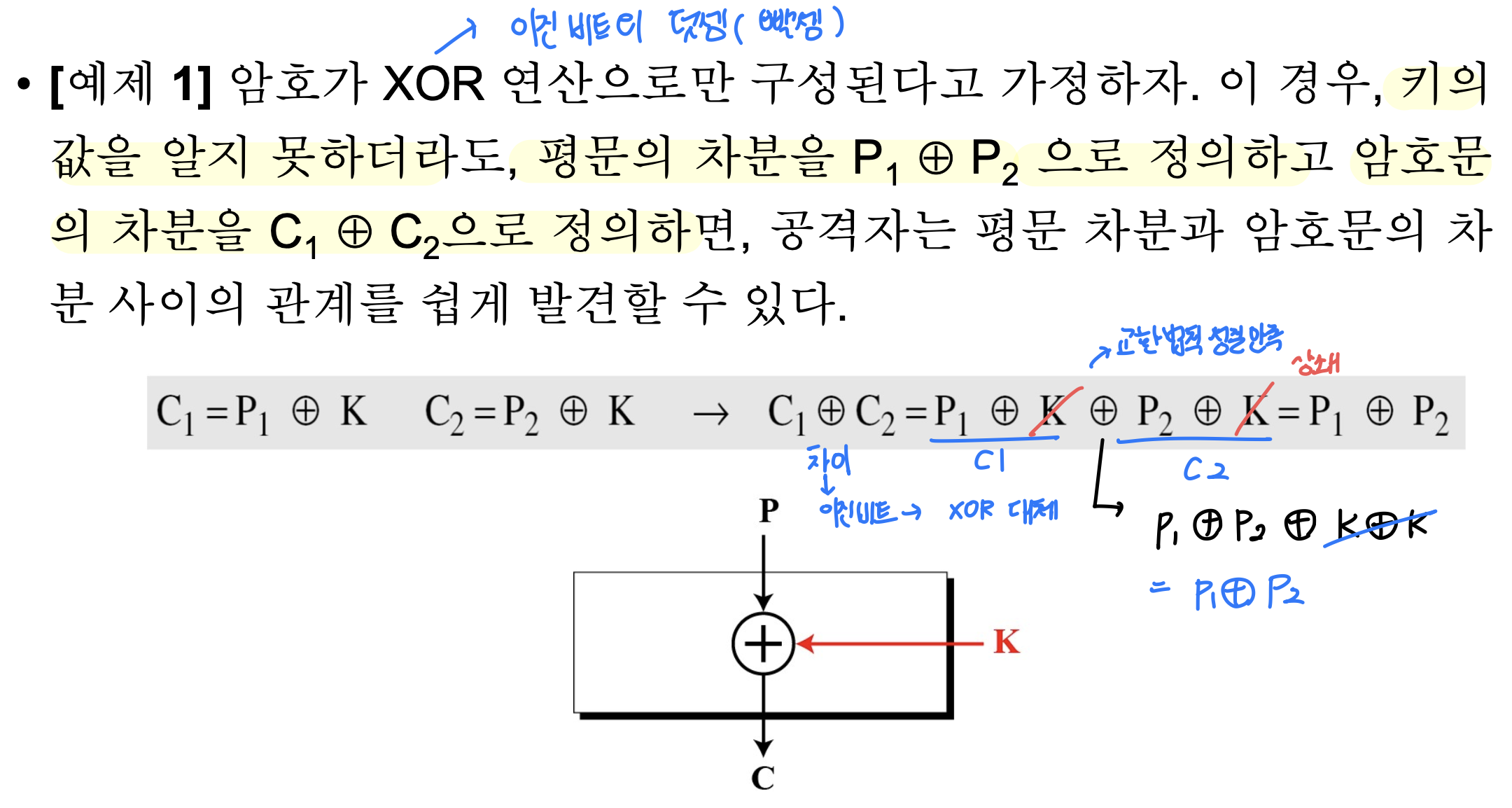
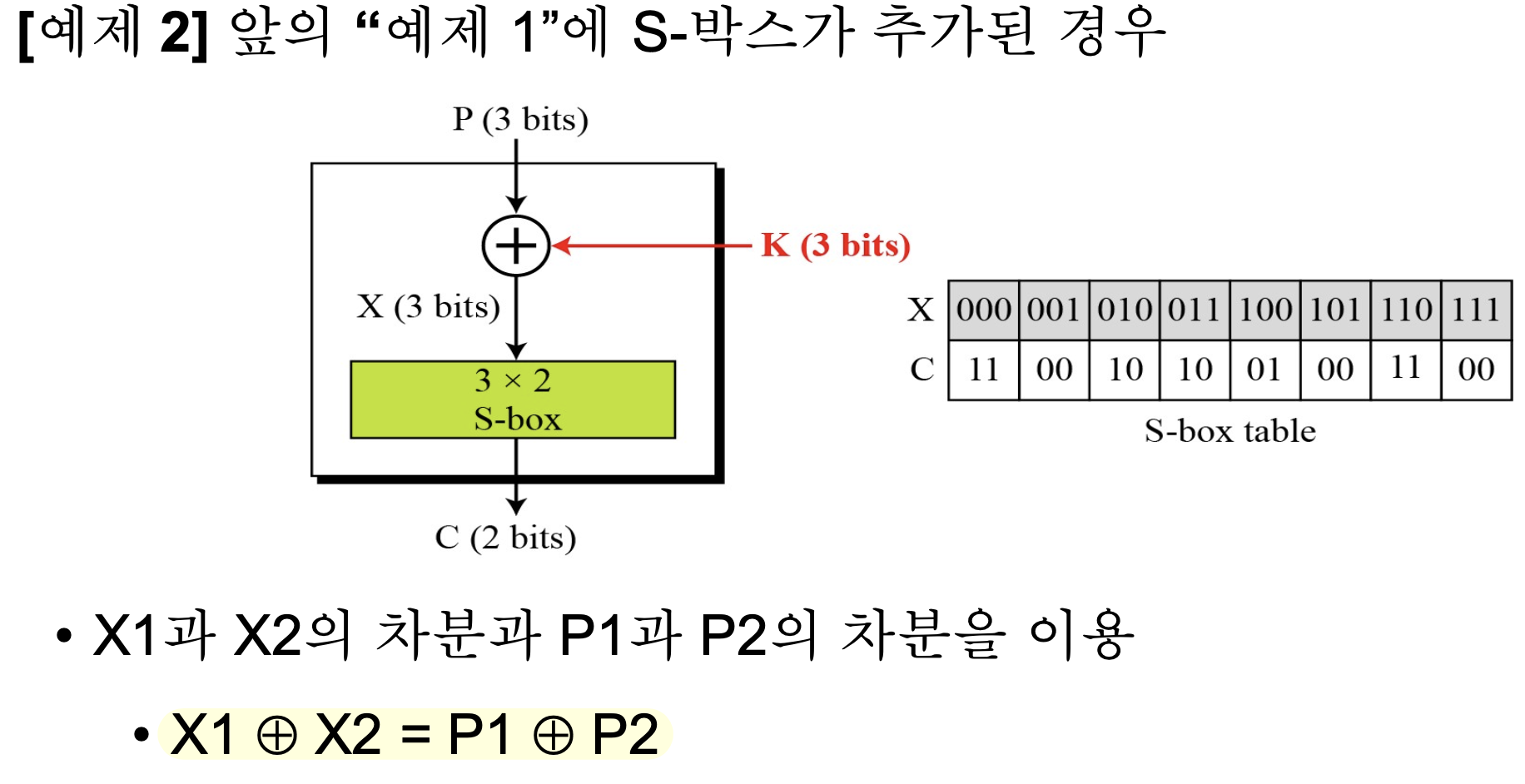
- 공격자는 암호가 각 평문의 차분에 대해 얼마나 많은 암호문 차분을 발생시키는지 확률적 관계를 분석하기 위해 다음과 같이 암호에 대한 입/출력 차분표를 만들 수 있음
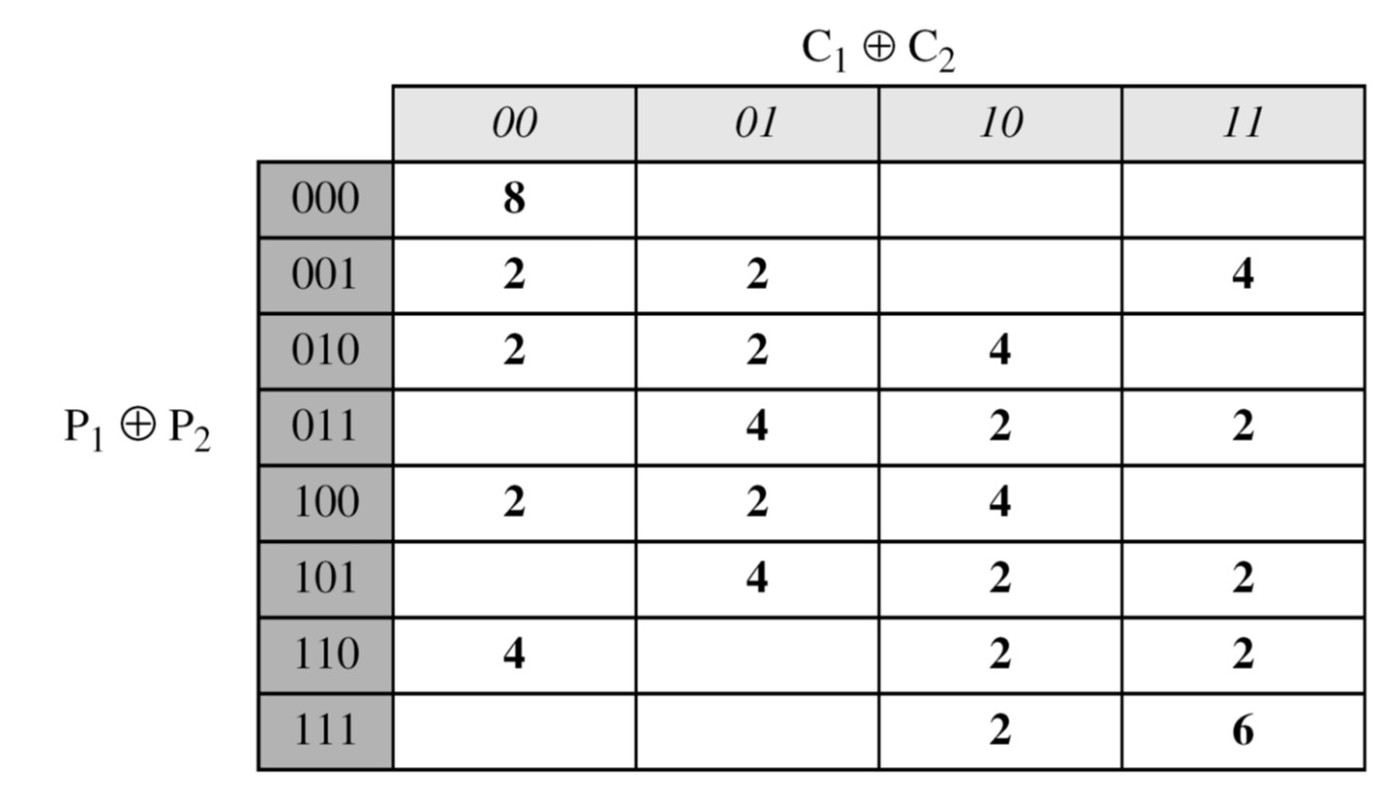
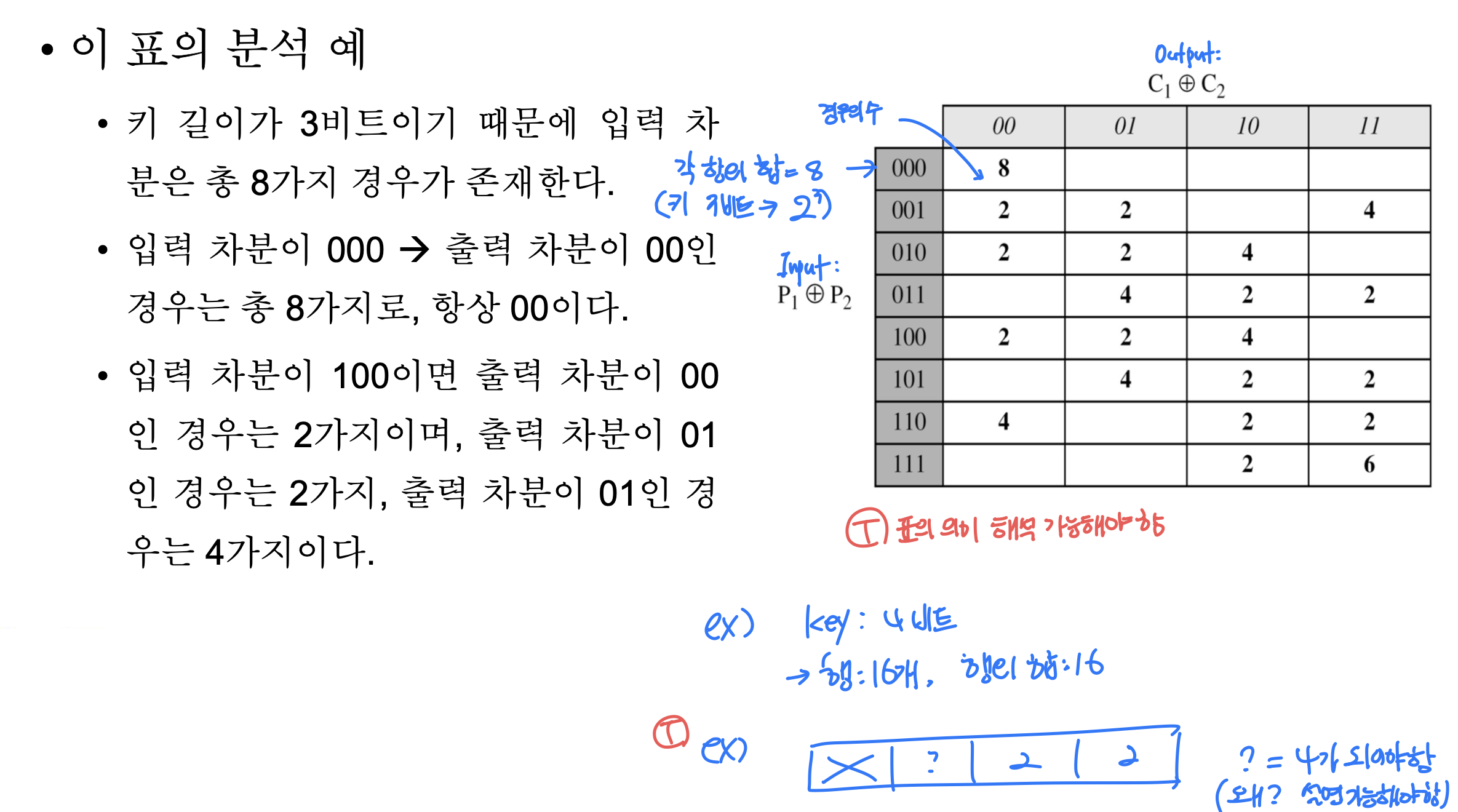
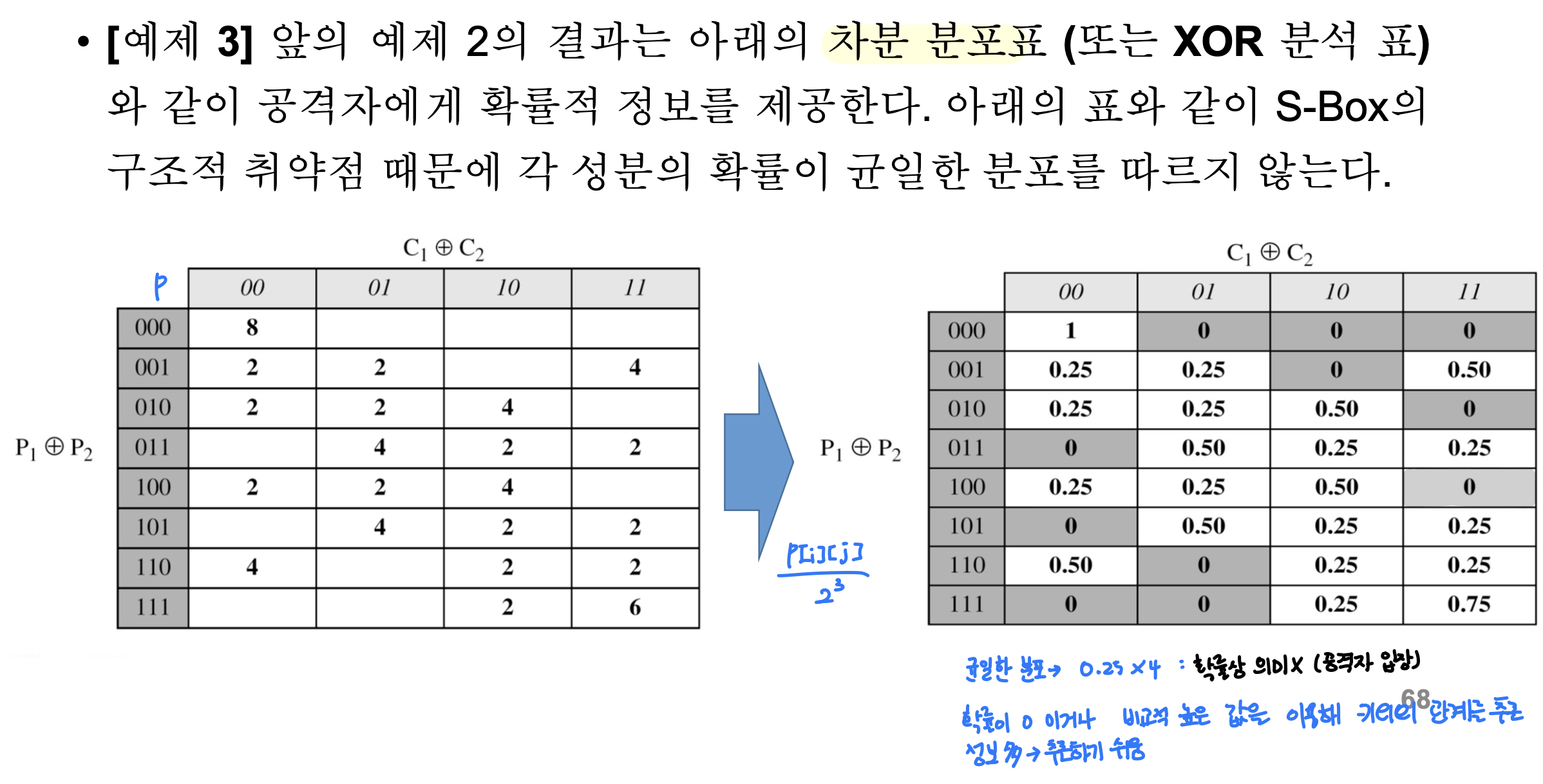
- 차분 분석 - 선택 평문 공격의 시작
- 공격자는 공격을 위해 필요한 평문의 차분을 선택함
- 공격자는 앞서 설명한 차분 확률 분포표를 참조해 가장 높은 확률을 갖는 평문의 차분을 선택할 수 있음
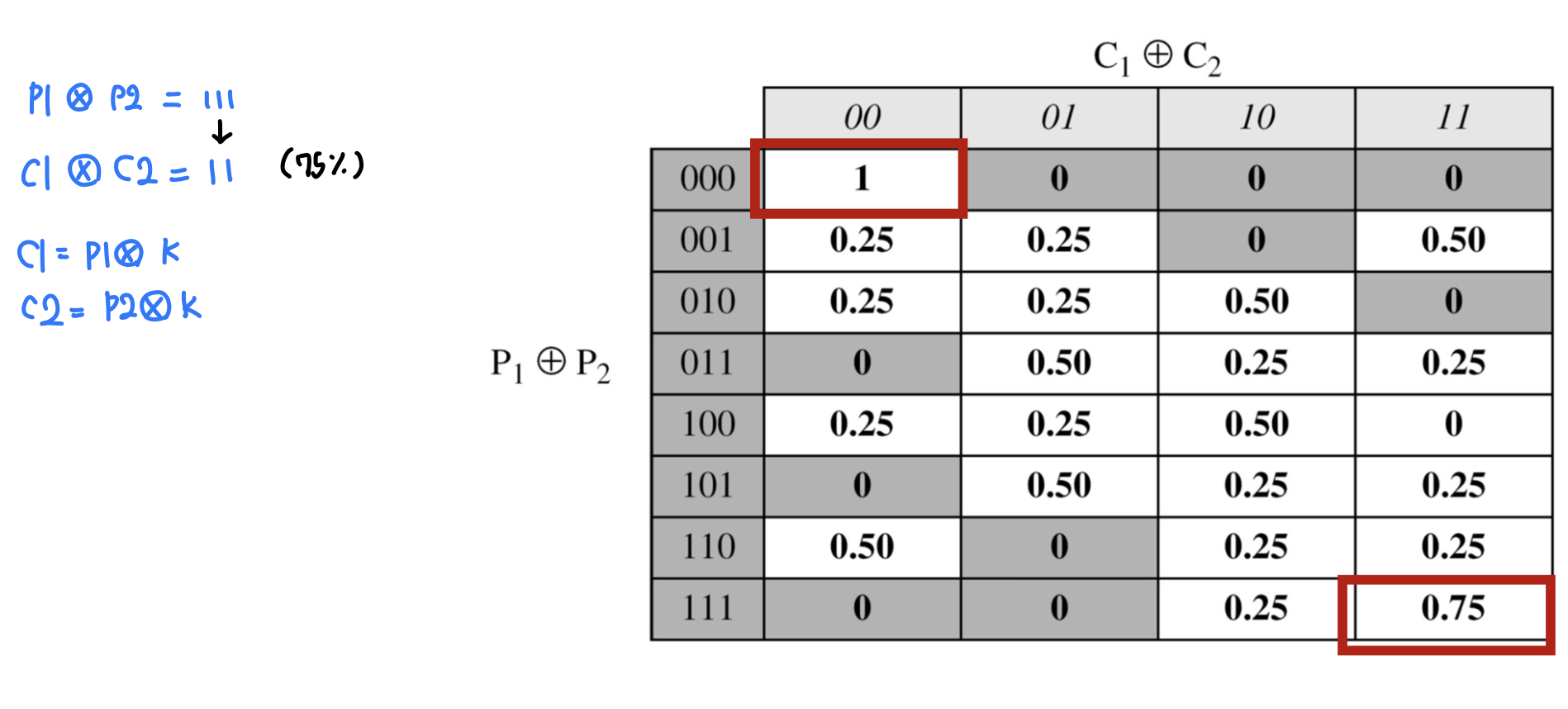
- 차분 분석 - 키 값 추측
- 공격자는 키 값을 추측하기 위해 선택한 특정 평문과 암호문 쌍을 찾음
- 선택 암호문 공격을 통해 암호문 C로부터 평문 P가 생성되도록 수행함
- 차분 분석의 일반적인 절차

선형 암호 분석(Linear Cryptanalysis)
- 기지 평문 공격(알려진 평문 공격) 이용
- 선형 S-Box를 갖는 간단한 암호 체계가 주어졌다고 가정할 때 c2c1c0은 암호문을 구성하는 각각의 비트를, p2p1p0은 평문을 구성하는 세 비트 각각을 나타냄
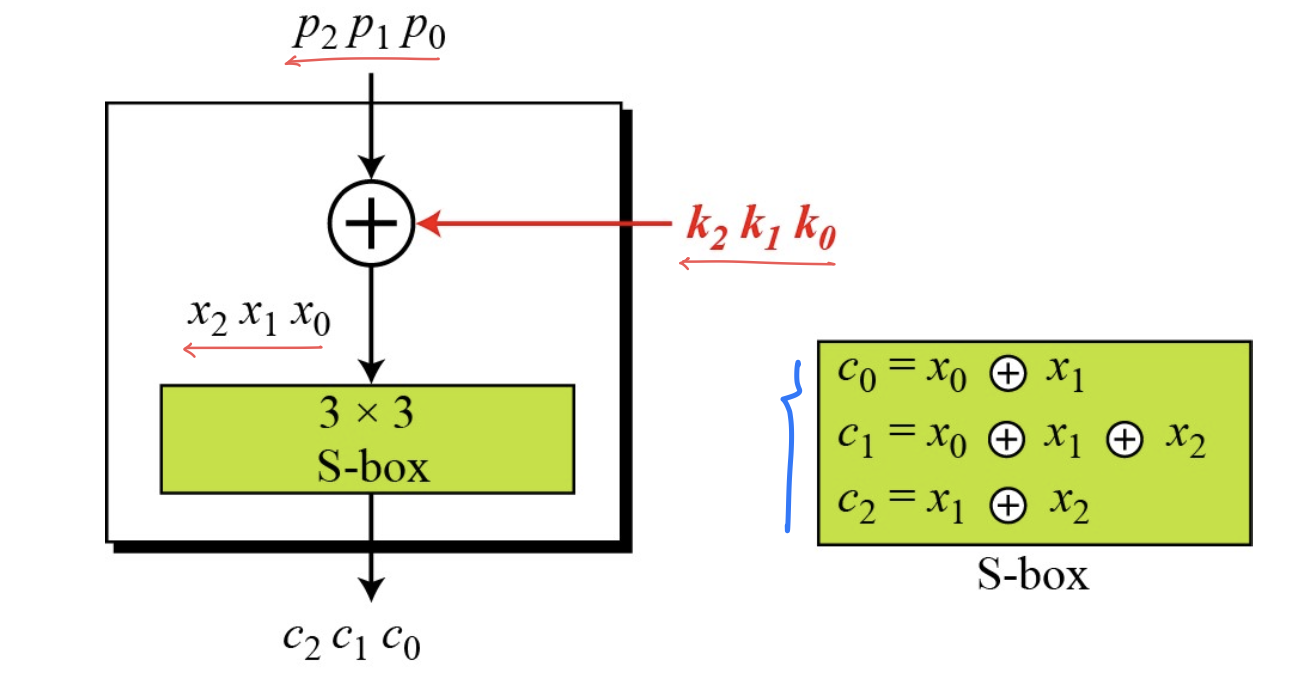
- 그러나 실제 블록 암호는 앞의 예제와 같이 간단하게 구현되지 않으며, 매우 많은구성요소들을 복합적으로 사용함
- 또한 S-Box는 일반적으로 선형으로 구성하지 않음
- 즉, 현대 블록 암호에서 S-Box는 완전한 선형함수가 아님
선형 근사(Linear Approximation)
- 현대 블록 암호에서 몇몇 S-Box는 특성 선형 함수에 의해 확률적으로 근사할 수 있음
- 일반적으로 n비트 평문과 암호문, 그리고 m비트 키가 주어지면 다음 형태의 수식을 찾을 수 있음
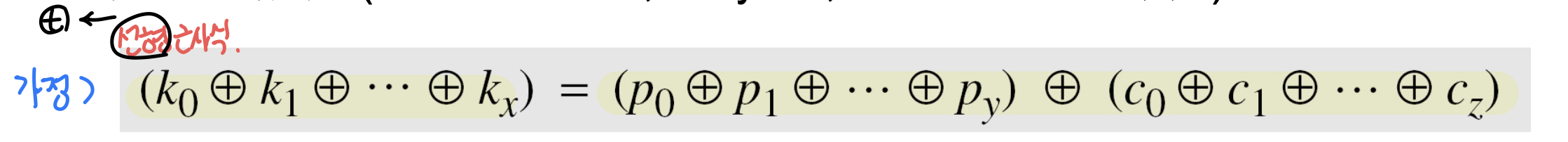
- 상기의 선형 근사식은 가로책 평문과 암호문의 비트는 키를 찾기 위해 사용될 수 있음
- 각 수식은 확률 1/2 + a를 반족해야함 (a = 편차)
