정보처리기사 실기 프로그래밍 기출 프로세스 스케줄링 FCFS / SJF / HRN / SRT / RR 문제 풀이

🔗 페이지교체 알고리즘 문제 풀기
정보처리기사 실기 프로그래밍 기출 프로세스 스케줄링 FCFS / SJF / HRN / SRT / RR 라운드로빈 문제 풀이

💡 프로세스 스케줄링 요약

FCFS : 먼저 들어온 일부터 처리
SJF : 실행시간이 짧은 일부터 처리
HRN : (대기시간+서비스시간)/서비스시간 결과값이 높은 값부터 처리
SRT : 실행시간이 빠른 일부터 선점형으로 처리

선점형 vs. 비선점형 스케줄링

• 선점 스케줄링 (preemptive scheduling)
  한 프로세스가 cpu를 할당받아서 실행하고 있을 때 다른 프로세스가 실행중인 작업을 중지시키고 cpu를 차지하는 기법

• 비선점 스케줄링(non-preemptive scheduling)
  이미 사용중인 cpu를 빼았지 못하고 사용이 끝날 때 까지 기다리는 스케줄링 기법
  

💡 FCFS(First Come First Served) 알고리즘

• 선착순 방식을 사용한 비선점 스케줄링 알고리즘
• = FIFO(First In First Out)

📝 문제풀이

다음과 같은 3개의 작업에 대하여 FCFS 알고리즘을 사용할 때, 임의의 작업 순서로 얻을 수 있는 최대 평균 반환시간을 T, 최소 평균 반환시간을 t라고 가정할 경우 T-t의 값은?

프로세스	실행시간
P1	9
P2	6
P3	12

최대 평균 반환시간 T 구하기

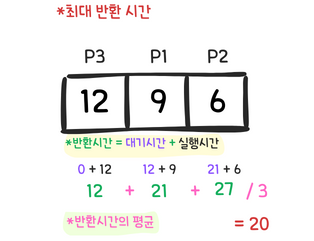
최대 평균 반환시간은 실행시간이 느린 것들부터 먼저 처리했을 경우의 반환시간을 말한다.

따라서 실행시간이 느린 순으로 나열하면 P3, P1, P2가 된다.

P3은 가장 먼저 들어왔으므로 대기 0초로 바로 시작하고, 자신을 12초만큼 실행한다. 그러면 반환시간은 대기 0 + 실행 12 = 12초가 된다.

FCFS는 비선점이므로 P3이 먼저 작업을 시작하면 실행이 끝날 때까지 다른 프로세스가 방해하지 못한다.

따라서 작업을 다 기다리면 P1은 P3이 작업한 만큼 12초를 대기하게 되고, 자신의 작업 9초를 실행하게 된다. 즉 P1의 반환시간은 대기 12초 + 실행 9초 = 21초가 된다.

P2도 마찬가지로 앞의 모든 작업을 기다리고서야 시작되므로 대기 시간 P1의 반환시간 21초 만큼을 전부 기다리고 그제서야 자기 작업 6초를 실행한다. 그러면 P2의 반환 시간은 21 + 6 = 27이 된다.

반환 시간의 평균을 구해야 하므로 반환시간을 모두 더하고, 프로세스의 개수 n으로 나눠야 한다. 따라서 최대 평균 반환시간은 아래와 같다.

(12 + 21 + 27) / 3 = 20

최소 평균 반환시간 t 구하기

최소 평균 반환시간은 반대로 실행시간이 빠른 것부터 처리한 후의 반환시간이다. 따라서 위에서 최대 반환시간을 구한 것과 같이 진행하되, 작업의 순서가 달라진다.

작업의 순서는 실행 시간이 작은 것부터 차례로 P2, P1, P3이며 계산은 생략한다. 따라서 최소 평균 반환시간은 아래와 같다.

(6 + 15 + 27) / 3 = 16

마지막으로 T - t를 하라고 했으므로 20 - 16이 답이 된다.

4

💡 SJF(Shortest Job First) 알고리즘

• 실행시간이 짧은 프로세스를 먼저 실행하는 방식
• 비선점형 스케줄링 방식

📝 문제풀이

다음은 프로세스가 준비 상태 큐에 도착한 시간과 프로세스를 처리하는데 필요한 실행 시간을 보여준다. 비선점형 SJF(Shortest Job First) 스케줄링 알고리즘을 사용할 경우, 프로세스들의 대기시간 총합을 구하시오. (단, 프로세스 간 문맥 교환에 따른 오버헤드는 무시하며, 주어진 4개 프로세스 외에 처리할 다른 프로세스는 없다고 가정한다)

프로세스	도착시간	실행시간
P1	0	30
P2	5	10
P3	10	15
P4	15	10

SJF는 비선점형이므로 한번 실행되면 중간에 뺄 수 없다.

도착시간이 없는 문제라면 무관하지만, 위와 같이 도착시간이 고려되는 문제의 경우 프로세스가 가장 먼저 도착하여 바로 실행할 수 있는 것이 최우선 순위가 된다.

따라서 실행시간이 가장 짧은 프로세스(SJF)가 아니더라도, 바로 작업을 시작할 수 있는 프로세스인 P1이 먼저 실행된다.

이제 실행시간이 짧은 순, 도착시간을 고려해서 프로세스 실행순서대로 정렬해보면 P1 - P2 - P4 - P3 순서가 된다.

프로세스 스케줄링의 최우선 순위*
만약 실행시간이 짧은 프로세스이더라도, 도착시간이 앞 프로세스 실행시간보다 늦을 경우에는 할당될 수가 없으므로 우선순위에서 밀려난다. 이는 바로 실행할 수 있는 작업이 최우선 순위라는 위의 설명과 같은 이치이다.

프로세스 실행순서대로 표를 다시 그려보자.

프로세스의 도착시간과 실행시간은 문제에서 주어진 값이고, 이 문제에서는 전체 프로세스의 대기시간을 알아야 한다. 반환시간은 답을 구하는데 필요 없지만 다른 문제에서 출제될 수 있으므로 함께 넣는다.

사실 프로세스가 처리되는 순서만 잘 정렬했다면 게임 끝이다. 더하기 빼기만 남았다.

프로세스	도착시간	실행시간	대기시간	반환시간
P1	0	30	0	0 + 30 = 30
P2	5	10	30 - 5 = 25	10 + 25 = 35
P4	15	10	(30 + 10) - 15 = 25	10 + 25 = 35
P3	10	15	(30 + 10 + 10) - 10 = 40	40 + 15 = 55

대기시간 구하는 법은 아래와 같다.

대기시간 = 이전 프로세스들의 실행시간 - 자신의 도착시간

예로 P1의 대기시간은 0이다. 이전에 할당된 프로세스가 없기 때문에 대기시간 없이 바로 실행되기 때문이다.

P2의 대기시간은 이전 프로세스인 P1의 실행시간에 본인의 도착시간을 뺀 만큼이다. P3, P4의 대기시간도 마찬가지로 구할 수 있다.

그럼 이 대기시간들을 다 더하면 문제의 요구사항이 충족된다. 정답은 아래와 같다.

90

이 문제에는 반환시간을 구하라는 요구는 없지만, 반환시간을 묻는 문제도 있으니 알아두자.

반환시간 = 대기시간 + 실행시간

💡 HRN(Highest Response-ratio Next) 알고리즘

• 응답률이 높은 작업부터 처리하는 알고리즘
• (대기시간+서비스시간)/서비스시간의 결과값이 높은 값부터 처리하는 방식

📝 문제풀이

HRN 방식으로 스케줄링 할 경우, 입력된 작업이 다음과 같을 때 우선순위가 높은 순서부터 차례로 옳게 나열하라.

프로세스	대기시간	서비스(실행)시간
A	40	20
B	20	20
C	70	10
D	120	30

말그대로 위의 공식을 대입하여 계산한 결과에서 값이 높은 것이 우선순위이다. 아래와 같이 나타낼 수 있다.

프로세스	우선순위
A	(40 + 20) / 20 = 3
B	(20 + 20) / 20 =2
C	(70 + 10) / 10 = 8
D	(120 + 30) / 30 = 5

높은 순으로 나열하면 정답은 아래와 같다.

C -> D -> A -> B

💡 SRT(Shortest Remaining Time) 알고리즘

• 실행시간이 빠른 작업부터 처리하는 SJF 기법을 선점형으로 전환한 형태
• 현재 작업중인 프로세스와 대기 큐의 프로세스의 실행시간을 비교하여 남은 실행시간이 더 적은 작업을 먼저 처리

📝 문제풀이

다음은 프로세스가 준비 상태 큐에 도착한 시간과 프로세스를 처리하는 데 필요한 실행시간을 보여준다. 선점형 스케줄링 알고리즘은 SRT 알고리즘을 사용할 경우, 프로세스들의 대기시간 총합은? (단, 프로세스 간 문맥 교환에 따른 오버헤드는 무시하며, 주어진 4개의 프로세스 외에 처리할 다른 프로세스는 없다고 가정한다)

프로세스	도착시간	실행시간
P1	0	30
P2	5	10
P3	10	15
P4	15	10

앞의 SJF 문제와 같은데, 알고리즘만 SRT로 바뀐 경우다. 여기서 선점형의 작업 방식을 확인할 수 있다. 어떻게 다른 결과가 나오는지 알아보자.

프로세스	P1	P2	P4	P3	P1
수행시간	5	10	10	15	25
남은시간	25	0	0	0	0

일단 가장 먼저 도착해있는 P1이 들어간다. 그런데 P1이 수행하고 5초 지나자 P2가 도착하는데, P2를 보니 실행시간이 10초라서 이미 실행중인 P1의 전체 실행시간 30-5=25를 하고도 P2보다 작업시간이 길다. 그러면 선점형 스케줄링은 이걸 교체해버린다. 즉 실행 중이지만 실행시간이 더 많이 남은 P1을 중단시키고 P2를 실행시키는 거다.

그러면 P2를 실행중이다. 실행하다보면 또 얼마 후에 P3이 도착하는데 이때도 둘의 실행시간을 비교한다. P2는 실행시간 10초에서 P3의 도착시간 -5를 해서 5초 가량만 남아있고, P3은 실행시간이 15초로 길기 때문에 교체 대상에서 제외된다.

P1 - P2 까지의 총 실행시간 5 + 10이 지나고 나면 P4가 도착하는데, 대기큐에 남아있던 P1의 나머지 작업 25초, P3의 작업 15초, P4의 작업 10초를 비교해서 가장 짧은 P4가 선점한다.

그러면 P1 - P2 - P4 순서로 프로세스를 바꿔 수행하고, P4 실행이 끝났을 때 P3을 실행한다. 그리고 마지막 남은 P1을 다시 실행하고 모든 프로세스가 종료된다.

모든 작업의 순서를 알았으니 대기시간을 구해보자. 선점형 스케줄링의 대기시간을 구할 때는 명심할 점이 있다. 자신의 모든 작업을 제외(조각난 작업 포함)하고, 그 앞에 실행된 작업시간들을 모두 더하면 된다.

아래 표는 프로세스가 처리되는 순서대로 각 시간을 정리한 표이다.

프로세스	P1	P2	P4	P3	P1
수행시간	5	10	10	15	25
도착시간	0	5	15	10	0
대기시간		5 - 5 = 0	(5 + 10) - 15 = 0	(5 + 10 + 10) - 10 = 15	(10 + 10 + 15) - 0 = 35
반환시간		10 + 0 = 10	10 + 0 = 10	15 + 15 = 30	25 + 35 = 65

여기서 주의깊게 볼 부분은 P1인데, P1은 처음 작업을 수행하다가 P2에게 선점당한 후 마지막에 다시 남은 작업을 처리하게 됐기 때문에 대기시간을 구할 때 자기 자신의 수행시간을 제외한 나머지 이전 프로세스들의 수행시간을 더해야 한다는 점이다. 실수하지 않도록 유의하자.

정답은 아래와 같다.

50

💡 RR(Round Robin) 알고리즘

• FCFS를 선점 형태로 변형한 기법
• 대기 큐에 도착한 순서에 따라 차례로 CPU 할당
• 각 프로세스는 할당된 시간 만큼만 실행 후 다음 프로세스에 CPU를 넘겨주고 완료되지 않았을 경우 큐의 가장 뒷자리에 배치됨

라운드 로빈 문제풀 때*
실행이 끝난 작업의 시간과 다음 들어올 작업의 도착시간을 비교하여 대기 큐를 쌓을 것!

📝 문제풀이

다음 표에서 보인 4개의 프로세스들을 시간 할당량(Time Quantum)이 5인 라운드 로빈(Round Robin)스케줄링 기법으로 실행시켰을 때 평균 반환시간을 구하시오.

프로세스	도착시간	실행시간
P1	0	10
P2	1	15
P3	3	6
P4	6	9

라운드 로빈 기법은 특정 시간 할당량을 두고 순서대로 작업을 수행하고 넘긴다. 이와 관련해 문제를 풀 때 주의할 것은, 프로세스는 순서대로 넘어가지만 그 순서가 왔을 때 다음 작업이 대기 큐에 있어야만 실행한다는 것이다. 그렇지 않다면 실행이 끝난 프로세스가 대기 큐에 쌓이게 된다.

문제를 통해 이 부분을 확인해보자.

프로세스	P1	P2	P3	P1	P4	P2	P3	P4	P2
수행시간	5	5	5	5	5	5	1	4	5
남은시간	5	10	1	5	4	5	0	0	0

일반적으로 차례로 할당한다고 하면 P1 - P2 - P3 - P4가 들어오고 작업이 끝날 때까지 순서대로 작업큐에 들어와야겠지만 위의 표는 그렇게 되지 않고 있다. P1 - P2 - P3 - P1 - P4의 작업 순서인 것을 볼 수 있다.

이는 P1이 5초 실행할 동안 P4가 대기큐에 도착해있지 않기 때문이다. P4는 도착시간이 6초이므로 P1의 할당시간 5초가 끝나고 대기큐에 먼저 올라가고 난 후에야 도착한다.

나머지는 할당량 5초 내에서 순서대로 쌓이며 작업을 마치게 된다. 대기시간과 반환시간을 구해보면 아래와 같다.

프로세스	도착시간	실행시간	대기시간	반환시간
P1	0	10	10 - 0 = 10	10 + 10= 20
P2	1	15	25 - 1 = 24	15 + 24 = 39
P4	3	6	25 - 3 = 22	6 + 22 = 28
P3	5	9	26 - 6 = 20	20 + 9 = 29

그리고 반환시간의 평균은 (20 + 39 + 28 + 29) / 4로 아래와 같다.

29

🙋🏻‍ 참고한 곳
🔗 홍달쌤 유튜브 🔗 홍달쌤의 정보처리기사 실기 책
🔗 스케줄링 기법(선점 스케줄링, 비선점 스케줄링)
🔗 [운영체제] FCFS 스케줄링 알고리즘 vs RR 스케줄링 알고리즘
🔗 프로세스 선점/비선점 스케줄링 기법