탐색

• 여러 개의 자료 중에서 원하는 자료를 찾는 작업
• 컴퓨터가 가장 많이 하는 작업 중의 하나
• 탐색을 효율적으로 수행하는 것은 매우 중요
• 탐색키(search key)
  - 항목과 항목을 구별해주는 키
• 탐색을 위하여 사용되는 자료구조
  - 배열, 연결 리스트, 트리, 그래프 등
  

순차 탐색

• 탐색 방법 중에서 가장 간단하고 직접적인 탐색 방법
• 정렬되지 않는 배열을 처음부터 마지막까지 하나씩 검색하는 방법
• 평군 비교 횟수
  - 탐색 성공 : (n + 1) / 2 번 비교
  • 탐색 실패 : n 번 비교

int seq_search(int key, int low, int high){
	int i;
    for( i = low; i <= high; i++ ){
    	if( list[i] == key )
        	return i;
    return -1;
}

개선된 순차 탐색

반복문의 리스트 끝 테스트 배제

• 리스트 끝에 탐색 키 저장
• 키 값을 찾을 때 반복문 탈출

int seq_search2(int key, int low, int high){
	int i;
    list[high+1] = key;
    for(i = low; list[i] != key; i++){
    	if( i = low; list[i] != key; i++ )
        	return -1;
        else
        	return i;
    }
}

이진탐색

• 정렬된 배열의 탐색에 적합
• 배열의 중앙에 있는 값을 조사하여 찾고자 하는 앙목이 왼쪽 또는 오른쪽 부분 배열에 있는지를 알아내어 탐색의 범위를 반으로 줄여가며 탐색 진행

이진 탐색의 알고리즘

재귀

int search_binary(int key, int low, int high){
	int middle;
    if( low <= high ){
    	middle = (low + high) / 2;
        if( key == list[middle] )
        	return middle;
        else if(key < list[middle] )
        	return search_binary(key, low, middle-1);
        else
        	return search_binary(key, middle+1, high);
    }
    return -1;
}

반복

int search_binary2(int key, int low, int high){
	int middle;
    while( low <= high ){
    	middle = (low + high) / 2;
        if( key == list[middle] )
        	return middle;
        else if( key > list[middle] )
        	low = middle + 1;
        else
        	high = middle - 1;
    }
    return -1;
}

색인 순차탐색

• 인덱스(index) 테이블을 사용하여 탐색의 효율 증대
  - 주 자료 리스트에서 일정 간격으로 발췌한 자료 저장
• 주 자료 리스트와 인덱스 테이블은 모두 정렬되어 있어야 함

보간 탐색

• 사전이나 전화번호부를 탐색하는 방법
  - 'ㅎ'으로 시작하는 단어는 사전의 뒷부분에서 찾음
  • 'ㄱ'으로 시작하는 단어는 앞부분에서 찾음
• 탐색키가 존재할 위치를 예측하여 탐색하는 방법
• 보간 탐색은 이진 탐색과 유사하나 리스트를 불균등 분할하여 탐색
• 보간 탐색은 데이터가 균등하게 분포되어 있을 때 유리

균형 이진 탐색 트리

이진 탐색과 이진 탐색 트리의 차이점

• 이진 탐색과 이진 탐색 트리는 근본적으로 같은 원리에 의한 탐색 구조
• 이진 탐색은 자료들이 배열에 저장되어 있으므로 삽입/삭제가 매우 비효율
  - 자료의 삽입/삭제 시 원소들을 모두 이동시켜야 함
• 이진 탐색 트리는 매우 빠르게 삽입/삭제 수행
• 삽입, 삭제가 빈번히 이루어진다면 이진탐색트리가 유리함

AVL 트리

• 모든 노드의 왼쪽과 오른쪽 서브트리의 높이 차가 1이하인 이진탐색트리

• 트리가 비균형 상태로 되면 스스로 노드들을 재배치하여 균형 상태 유지

• 균형 인수
  = (왼쪽 서브 트리의 높이 - 오른쪽 서브 트리의 높이)

• 모든 노드의 균형 인수가 +-1 이하면 AVL 트리

AVL 트리 연산

• 탐색 연산 : 이진탐색트리와 동일
• 삽입 연산과 삭제 연산 시 균형 상태가 깨질 수 있음
• 삽입 연산
  - 삽입 위치에서 루트까지의 경로에 있는 조상 노드들의 균형 인수 영향
  • 삽입 후에 불균형 상태로 변한 가장 가까운 조상 노드(균형 인수가 +-2가 된 가장 가까운 조상 노드의 서브 트리들에 대하여 다시 재균형
  • 삽입 노드부터 균형 인수가 +-2가 된 가장 가까운 조상 노드까지 회전

삽입 연산

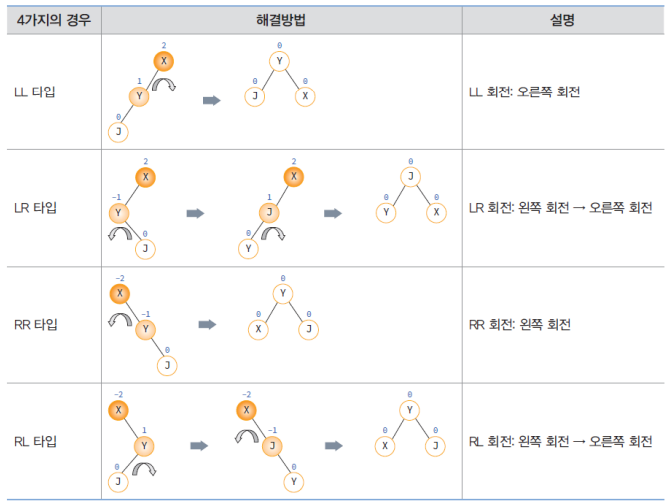
구조체

typedet struct AVLNode{
	int key;
    struct AVLNode *left;
    struct AVLNode *right;
} AVLNode;

LL 회전 방법

AVLNode *rotate_right(AVLNode *parent){
	AVLNode *child = parent->left;
    parent->left = child->right;
    child->right = parent;
    
    return child;
}

RR 회전 방법

AVLNode *rotate_left(AVLNode *parent){
	AVLNode *child = parent->right;
    parent->right = child->left;
    child->left = parent;
    
    return child;
}

LR 회전 방법

AVLNode *rotate_left_right(AVLNode *parent){
	parent->left = rotate_left(parent->left);
    return rotate_right(parent);
}

RL 회전 방법

AVLNode *rotate_right_left(AVLNode *parent){
	parent->right = rotate_right(parent->right);
    return rotate_left(parent);
}