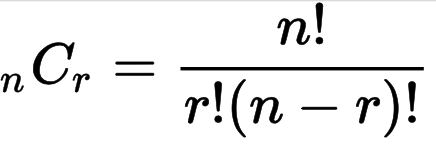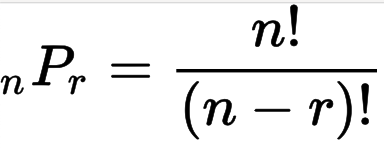TIL_ Algorithm

Today 공부
- 순열 / 조합
- GCD / LCM
- 멱집합
순열/조합
순열 : n개 중에서 일부만을 선택해서 순서를 지키면서 나열
- 순열은 일반화 과정을 거쳐, Permutation의 약자 P로 표현합니다.
- 일반식 : nPr = n! / (n - r)!
- ex) 5장에서 3장을 선택하는 모든 순열의 수
= 5P3 = (5 X 4 X 3 X 2 X 1) / (2 X 1) = 60
조합 : n개 중에서 순서를 생각하지 않고 나열
* 순열로 구할 수 있는 경우를 찾습니다.
* 순열로 구할 수 있는 경우에서 중복된 경우의 수를 나눕니다.
- 조합은 일반화 과정을 거쳐, Combination의 약자 C로 표현합니다.
- 일반식: nCr = n! / (r! * (n - r)!)
- ex) 5장에서 3장을 무작위로 선택하는 조합에서 모든 경우의 수
= 5C3 = 5! / (3! * 2!) = 10
조합공식 순열공식
GCD/LCM
| - | - |
|---|---|
| 약수 | 어떤 수를 나누어떨어지게 하는 수 |
| 배수 | 어떤 수의 1, 2, 3, ...n 배하여 얻는 수 |
| 공약수 | 둘 이상의 수의 공통인 약수 |
| 공배수 | 둘 이상의 수의 공통인 배수 |
| 최대 공약수(GCD) | 둘 이상의 공약수 중에서 최대인 수 |
| 최소 공배수(LCM) | 둘 이상의 공배수 중에서 최소인 수 |
GDC
나누어서 나머지가 없이 떨어지는 수들을 나열한 뒤,
공통된 수만 모으면 공약수를 구할 수 있습니다.
멱집합
어떤 집합이 있을 때, 이 집합의 모든 부분집합을 멱집합이라 합니다.
집합 {1, 2, 3}의 모든 부분집합은 {}, {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}, {1, 2, 3} 으로 나열할 수 있고, 이 부분집합의 총 개수는 8개입니다. 그리고 이 모든 부분집합을 통틀어 멱집합이라고 합니다.
마치며,
알고리즘 문제에 수학적 개념이 필요할 때도 있다고 한다
이 부분을 문제에서 잘 파악하면 해결방안을 더 쉽게 이해 도출해 낼 수 있는거 같다.
알고리즘문제에서 자주 다루는 최소한의 수학을 익혀 적재적소에 활용할 수 있는 능력을 길러야 할 것 같다.