[Algorithm] Divide and Conquer

1. 분할정복(Divide and Conquer)

• 대표적인 알고리즘 설계 기법 중 하나
• 여러 알고리즘의 기본이 되는 해결방법으로, 기본적으로는 엄청나게 크고 방대한 문제를 조금씩 조금씩 나눠가면서 용이하게 풀 수 있는 문제 단위로 나눈 다음 그것들을 다시 합쳐서 해결하자는 개념
• 대표적인 알고리즘 설계 기법: 분할정복(divide-and-conquer) 방법, 동적 프로그래밍 방법(dynamic programming) 방법, 그리디(greedy) 방법

1-1) 분할정복 방법의 원리

• 순환적(recursive)으로 문제를 푸는 하향식(top-down)접근 방법
  : 주어진 문제의 입력을 더 이상 나눌 수 없을 때까지 순환적으로 분할하고 분할된 작은 문제들을 해결한 후 그 해를 결합하여 원래 문제의 해를 구하는 방식

1-2) 분할정복 방법의 특징

• 분할된 작은 문제는 원래 문제와 성격이 동일하다. -> 입력 크기만 작아짐
• 분할된 문제는 서로 독립적이다. -> 순환적 분할 및 결과 결합 가능

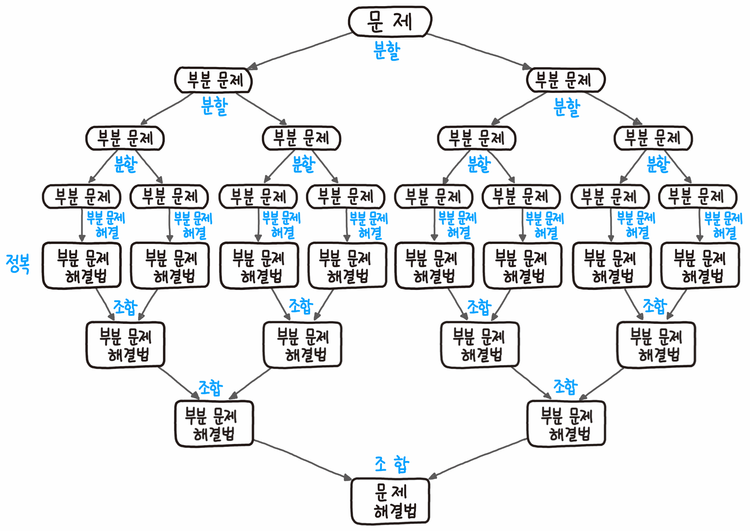
1-3) 분할정복 방법의 처리 과정: 분할 -> 정복 -> 결합

• 분할 정복은 상단에서 분할하고, 중앙에서 정복하고, 하단에서 결합하는 형태로 도식화 할 수 있다.

  • ⭐️분할: 문제를 더 이상 분할할 수 없을 때까지 동일한 유형의 여러 하위 단위로 나눈다.
  • ⭐️정복: 가장 작은 단위의 하위 문제를 해결하여 정복한다.
  • ⭐️결합: 하위 문제에 대한 결과를 원제 문제에 대한 결과로 조합한다.

[출처] 파이썬 알고리즘 인터뷰

1-4) 해당 강의록 부분 참고

Type D&C (P){
  if small(P) return solution(P); // 임계값보다 작다면 그냥 풀기
  else{ // 임계값보다 크면
    divide P into smaller instances P1, P2, ... , Pk (k>=1) // divide
    // divide D&C to Pi
    return combine(D&C(p1), ... , D&C(pk)); // merge (merge할 때에도 divide할 때와 마찬가지로 똑같이 적용 - recursive)
  }
}

---

2. 이진 탐색(Binary Search)

• 🔥정렬된 데이터🔥에 대한 효과적인 탐색🔍 방법
• 입력이 정렬된 리스트에 대해서만 적용 가능

2-1) 이진 탐색의 원리

• 배열의 가운데 원소와 탐색 키 x를 비교
• 1) 탐색 키 == 가운데 원소 ➡️ 탐색 성공
• 2) 탐색 키 < 가운데 원소 ➡️ '이진 탐색(크기 ½의 왼쪽 부분배열)' 순환 호출
• 3) 탐색 키 > 가운데 원소 ➡️ 이진 탐색(크기 ½의 오른쪽 부분배열)' 순환 호출

2-2) 이진 탐색의 특징

• 탐색을 반복할 때마다 대상 원소의 개수가 ½씩 감소
• ⭐️성능: Θ(logn)

2-3) 이진 탐색의 분할정복 과정

• 분할 정복은 상단에서 분할하고, 중앙에서 정복하고, 하단에서 조합하는 형태로 도식화 할 수 있다.

  ⭐️분할: 배열의 가운데 원소를 기준으로 왼쪽, 오른쪽 부분배열로 분할. 탐색 키와 가운데 원소가 같으면 반환 및 종료
  ⭐️정복: 탐색 키가 가운데 원소보다 작으면 왼쪽 부분배열을 대상으로 이진 탐색을 호출, 크면 오른쪽 부분배열을 대상으로 이진 탐색을 순환호출
  ⭐️조합: 탐색 결과가 직접 반환되므로 결합 불필요

2-4) 이진 탐색의 시간복잡도 분석

• 최악의 경우 시간복잡도 분석
  

• 시간복잡도: Θ(logn)

2-5) 이진탐색 코드

int BinarySearch(int left, int right, int target){
  if(left>right) return 0; // 못 찾은 경우
  else{
    int mid = (left+right)/2;
    
    if(target==v[mid]) return 1;
    else if(target<v[mid]) return BinarySearch(left, mid-1, target);
    else return BinarySearch(mid+1, right, target);
  }

}

---

3. 합병 정렬(Merge Sort)

• 기본적으로 🔥분할 정복🔥알고리즘을 기반으로 정렬되는 방식으로, 분할 정복 그 자체라고도 볼 수 있다.

3-1) 합병 정렬의 처리 과정: 분할 -> 정복 -> 결합

• 분할 정복은 상단에서 분할하고, 중앙에서 정복하고, 하단에서 결합하는 형태로 도식화 할 수 있다.

  • ⭐️분할: 입력 배열을 같은 크기의 2개의 부분 배열로 분할한다.
  • ⭐️정복: 부분 배열을 정렬한다. 부분 배열의 크기가 충분히 작지 않다면 순환 호출(recursive recursion)을 이용하여 다시 분할 정복 방법을 적용한다.
  • ⭐️결합: 정렬된 부분 배열들을 하나의 배열에 합병한다.
    (결합할 때에는 결합을 위한 임시 배열이 필요)

• 강의록 참조 설명

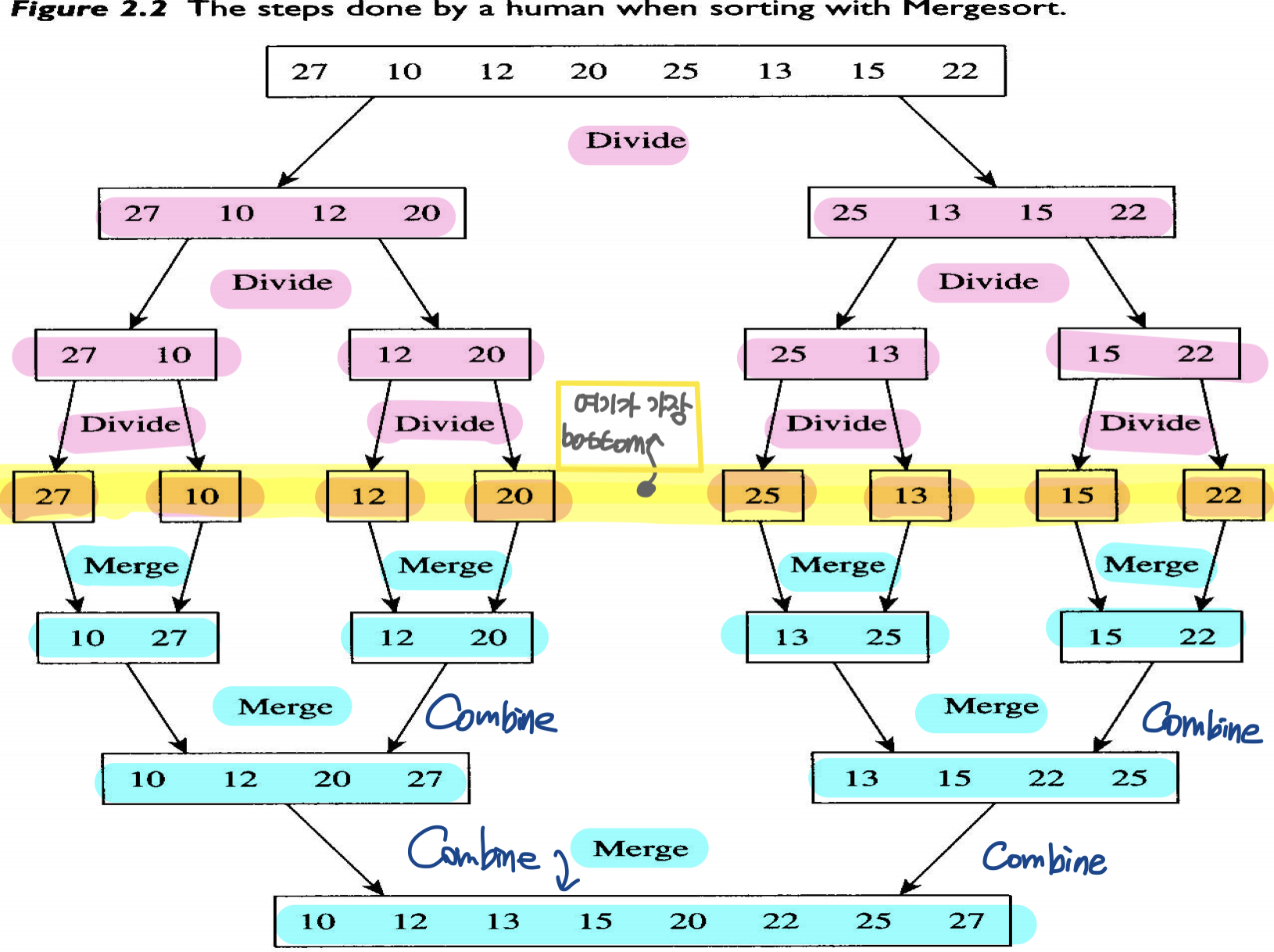
• Divide the array into two subarrays
• Conquer each subarray by sorting it (may use recursion)
• Combine the two subarrays by merging

• 강의록 그림 설명 참조

3-2) 합병 정렬 소스코드

• 강의 코드 -> Divide와 Combine의 과정을 두 개의 함수로 나눔.
• 내 코드 -> Divide와 Combine을 하나의 함수로 만들면 더 깔끔하지 않을까?

void mergeSort(int l, int r){ // l:left,  r:right를 의미
  if(l==r) return;

  int m = (l+r)/2;
  mergeSort(l, m);
  mergeSort(m+1, r); // Divide 끝

  // combine 수행
  vector<int> tmp; int i=l, j=m+1;
  while(i<=m && j<=r){
    if(a[i]<a[j]) tmp.emplace_back(a[i++]);
    else tmp.emplace_back(a[j++]);
  }
  while(i<=m) tmp.emplace_back(a[i++]);
  while(j<=r) tmp.emplace_back(a[j++]);

  for(int k=0, i=l; k<tmp.size(); k++) a[i++]=tmp[k]; // 배열에 원상 복귀
}

3-3) 합병 정렬 시간복잡도 분석

• merge할때의 time complexity 분석

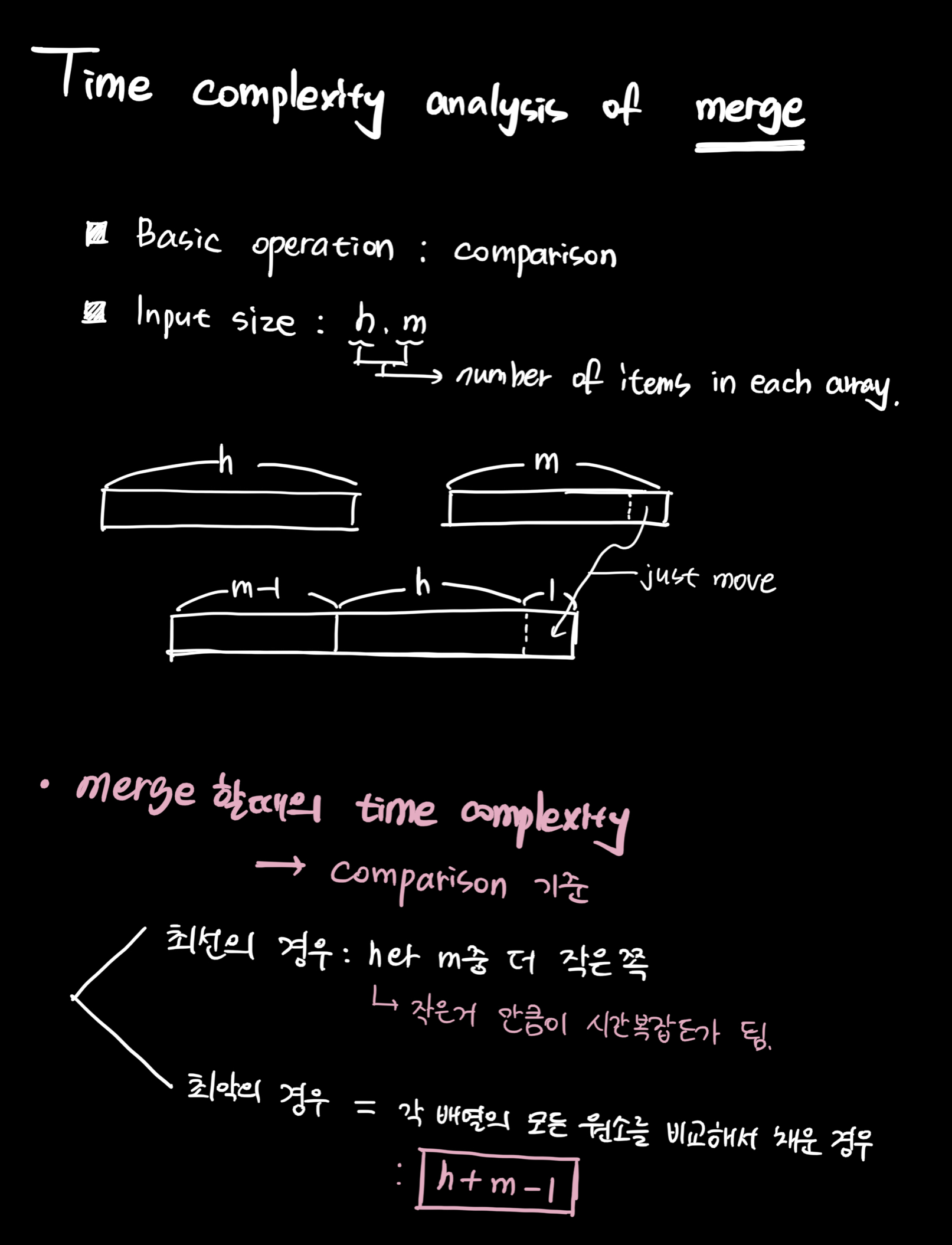
• worst case's time complexity analysis

위의 점화식을 풀고, W(n)에 대해서 정리하면
w(n) = nlogn - (n-1) 이 나오고 이는 nlogn의 시간복잡도라 할 수 있다.

병합 정렬 분석

• (최악의 경우) 시간복잡도: O(nlogn)
• 공간복잡도: O(n) -> n만큼의 공간 할당이 필요

---

4. 퀵 정렬(Quick Sort)

• 퀵 정렬도 🔥분할 정복🔥알고리즘을 기반으로 정렬되는 방식으로, 평균적으로 매우 빠른 수행 속도를 자랑하는 정렬 기법입니다
• 퀵 정렬은 불안정 정렬에 속하며, 다른 원소와의 비교만으로 정렬을 수행하는 비교 정렬에 속합니다
• 리스트 안에 pivot(피벗) 원소를 기준으로 pivoting이 진행되며, 한 번의 pivoting이 진행되고 나면 해당 pivot 원소는 자기 위치를 찾게 됩니다

4-1) 퀵 정렬의 처리 과정

• 먼저, 퀵 정렬은 🔥분할 정복🔥방법을 통해 리스트를 정렬합니다.

  • 1. 리스트 가운데서 원소를 하나 고릅니다. 이렇게 고른 원소를 피벗(pivot)이라고 합니다. (리스트의 가장 첫 원소를 피벗이라고 설정)
  • 2. 피벗 앞에는 피벗보다 값이 작은 모든 원소들이 오고, 피벗 뒤에는 피벗보다 값이 큰 모든 원소들이 오도록 피벗을 기준으로 리스트를 둘로 나눕니다.
       이렇게 리스트를 둘로 나누는 것을 분할이라고 합니다.
       분할을 마친 뒤에 피벗은 더 이상 움직이지 않습니다.
       -> (한 번의 pivoting이 완료된 후로, pivot 원소는 자기 위치를 찾게 됩니다.)
  • 3. pivot을 기준으로 분할된 두 개의 작은 리스트에 대해 재귀적으로 이 과정을 반복합니다.

✅ 재귀 호출이 한 번 진행될 때마다(한 번의 pivoting이 완료된 후) 피벗으로 정한 원소의 위치가 정해지게 됩니다

• 기존 내 풀이 방식

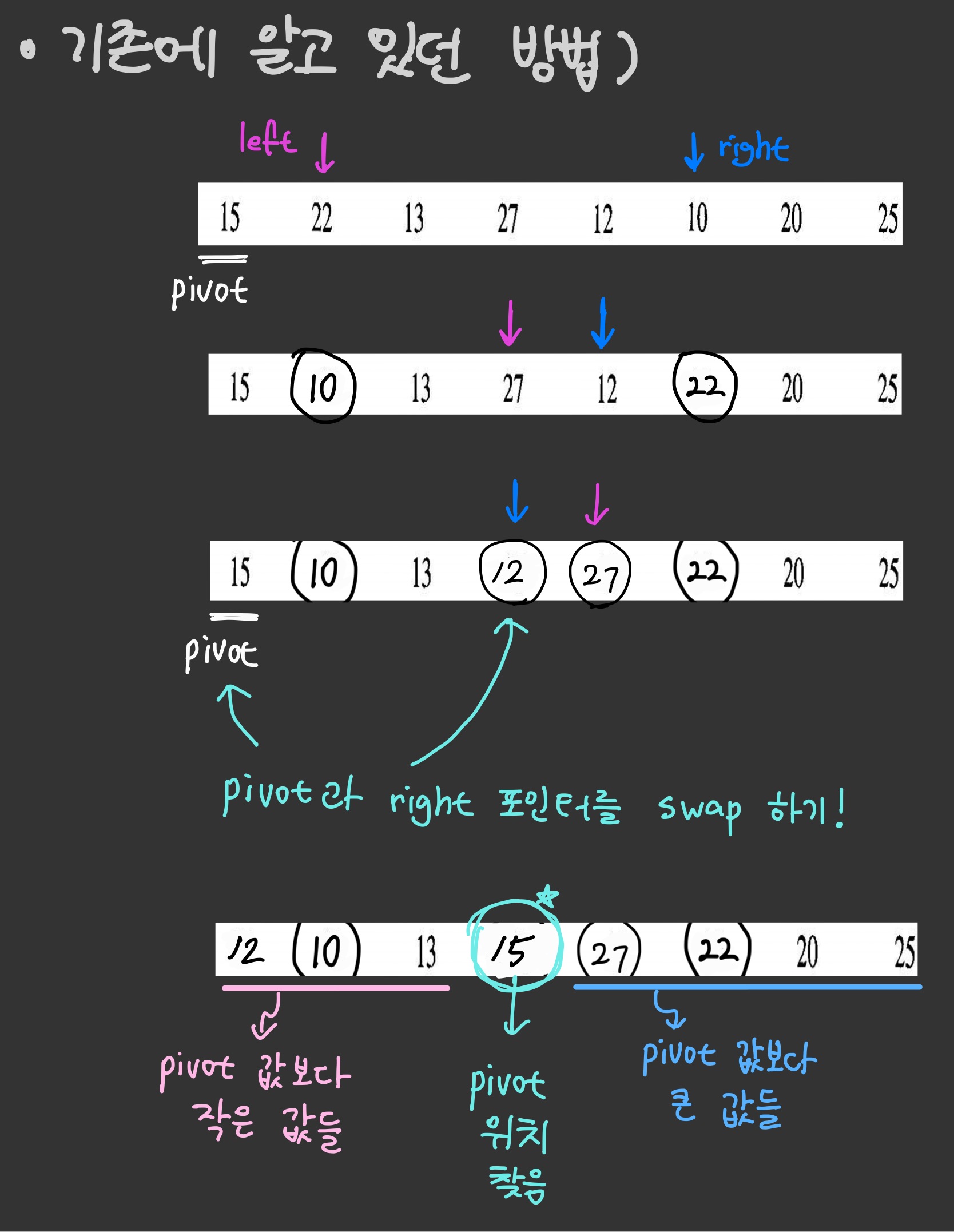
• 해당 소스코드

void quickSort(int l, int r){
  if(l>=r) return;
  else{
    int p1 = l+1, p2 = r;

    while(p1<=p2){
      while(a[p1]<a[l] && p1<=r) p1++;
      while(a[p2]>a[l] && l<=p2) p2--;

      if(p1<p2) swap(a[p1], a[p2]);
      else{
          swap(a[l], a[p2]);
          break;
      }
    }
    // 한 번의 pivoting 과정 수행

    if(l<p2-1) quickSort(l, p2-1);
    if(p2+1<r) quickSort(p2+1, r);
  }
}

• 새로운 방법 (강의록 내용)

• 해당 소스코드