[Algorithm] Sorting / Merge Sort

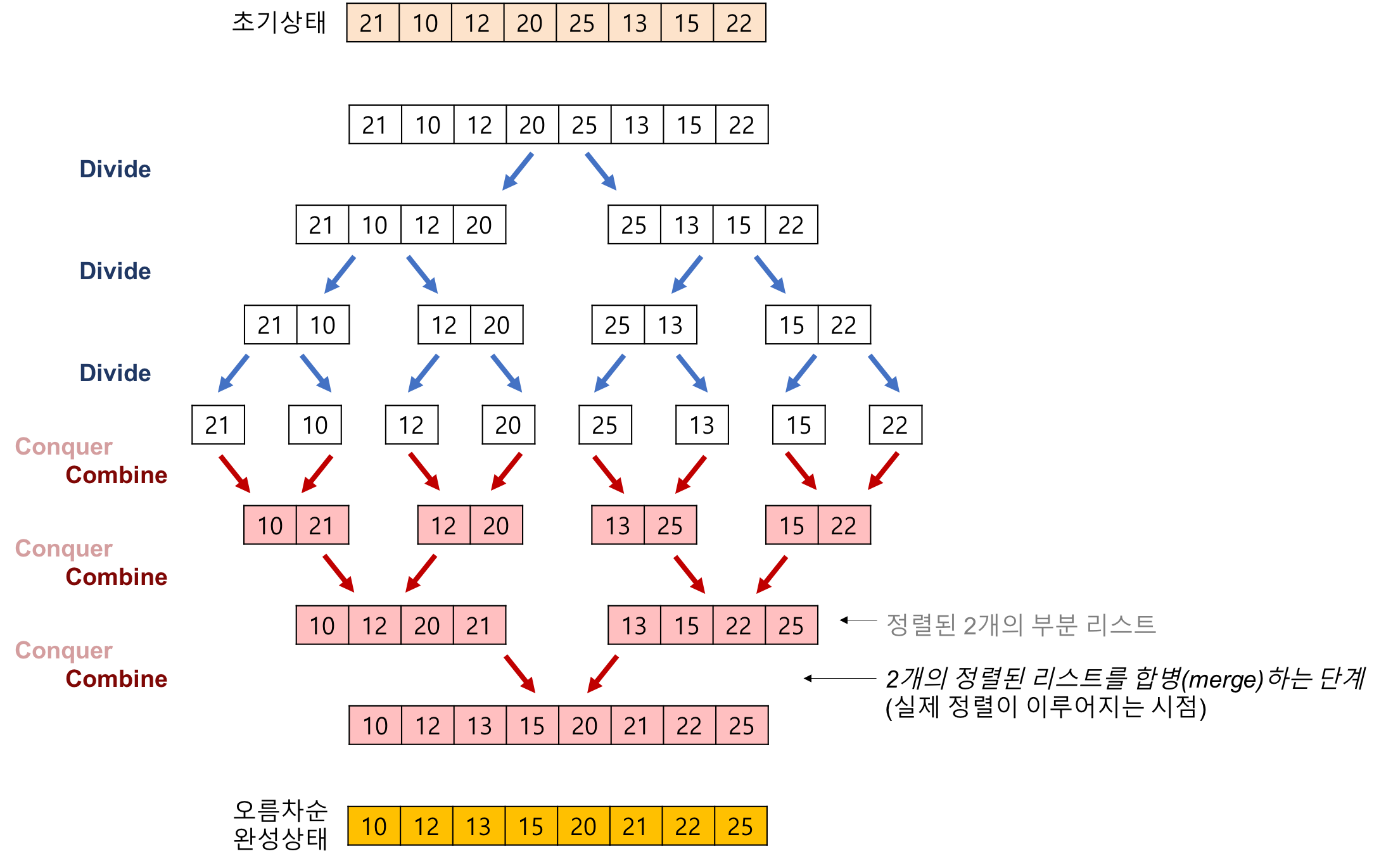
Merge Sort(합병 정렬)

• 합병 정렬은 기본적으로 '분할 정복' 알고리즘을 기반으로 정렬되는 방식이다.
• 합병 정렬은 다음의 단계들로 이루어진다.

  • 분할: 입력 배열을 같은 크기의 2개의 부분 배열로 분할한다.
  • 정복: 부분 배열을 정렬한다. 부분 배열의 크기가 충분히 작지 않으면 순환 호출을 이용하여 다시 분할 정복 방법을 적용한다.
  • 결합: 정렬된 부분 배열들을 하나의 배열에 합병한다.

분할 정복(Devide and Conquer)

• 여러 알고리즘의 기본이 되는 해결방법으로, 기본적으로는 엄청나게 크고 방대한 문제를 조금씩 조금씩 나눠가면서 용이하게 풀 수 있는 문제 단위로 나눈 다음 그것들을 다시 합쳐서 해결하자는 개념이다.
• 대표적으로는 퀵소트나 병합정렬이 있다.
• 분할 정복은 상단에서 분할하고, 중앙에서 정복하고, 하단에서 조합하는 형태로 도식화 할 수 있다.
• 분할: 문제를 더 이상 분할할 수 없을 때까지 동일한 유형의 여러 하위 단위로 나눈다.
• 정복: 가장 작은 단위의 하위 문제를 해결하여 정복한다.
• 조합: 하위 문제에 대한 결과를 원제 문제에 대한 결과로 조합한다.

분할 정복 알고리즘을 쉽게 나타낸 그림 도식표이다.

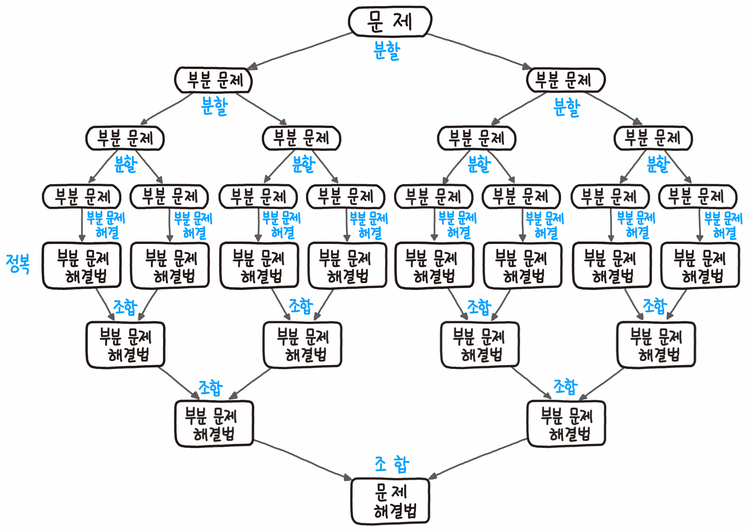
[출처] 파이썬 알고리즘 인터뷰

이미지 출처

합병 정렬의 알고리즘 코드는 다음과 같습니다.

#include <iostream>
using namespace std;

void MergeSort(int a[], int left, int right){
    if(left>=right) return; // 같을 때 주의!

    int mid = (left + right)/2;

    MergeSort(a, left, mid);
    MergeSort(a, mid+1, right);
    
    int i=left, j=mid+1, k=left;
    int tmp[14];
    while(i<=mid && j<=right){
        if(a[i]<a[j]){
            tmp[k++]=a[i++];
        }
        else{
            tmp[k++]=a[j++];
        }
    }
    while(i<=mid) tmp[k++]=a[i++];
    while(j<=right) tmp[k++]=a[j++];

    for(int i=left; i<=right; i++) a[i]=tmp[i]; // 원래 배열에 복원시키기
};

int main(){
    int a[14] = {20, 18, 1, 10, 5, 8, 7, 6, 4, 3, 2, 9, 17, 16};
    int n = 14;

    MergeSort(a, 0, 13);

    for(int i=0; i<n; i++) cout<<a[i]<<" ";
    cout<<endl;
    return 0;
}

합병 정렬의 시간복잡도

• 최상, 최악인 경우 모두 O(nlogn)
• 합병 정렬은 항상 O(nlogn)의 시간복잡도를 갖는다.

참고블로그링크