[Leetcode/C++] 33_Search in Rotated Sorted Array

문제는 다음과 같습니다.

문제링크

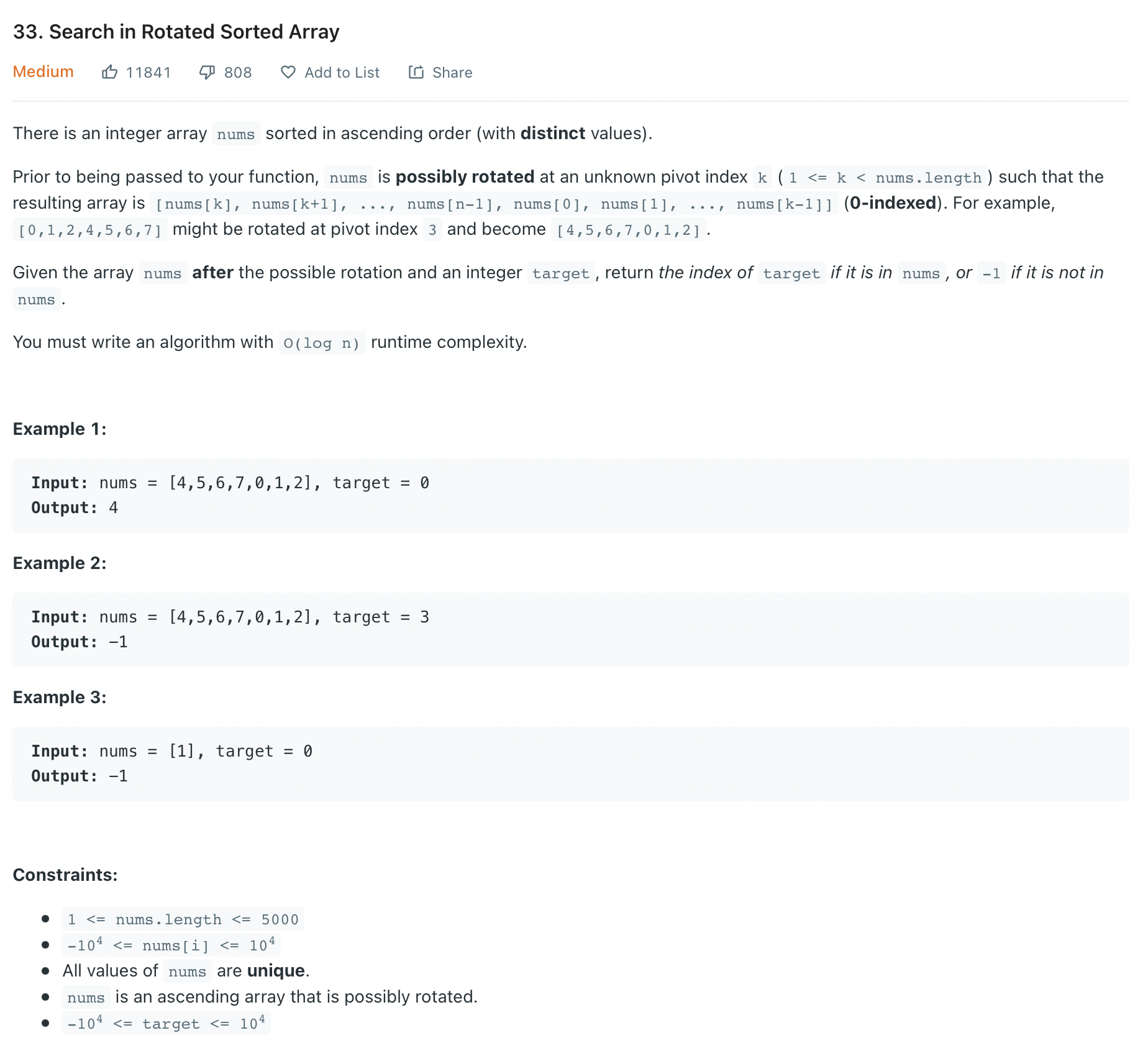
제 풀이는 다음과 같습니다.

class Solution {
public:
    int idx=-1;
    
    void BinarySearch(vector<int>& nums, int l, int r, int t){
        cout<<"l:"<<l<<", "<<"r: "<<r<<endl;
        if(l > r) return;
        
        if(nums[l]<=nums[r]){ // 경우1: 피벗 x -> 원래의 이진탐색과 같음
            int mid = (l+r)/2;
            if(t < nums[mid]) BinarySearch(nums, l, mid-1, t);
            else if (t > nums[mid]) BinarySearch(nums, mid+1, r, t);
            else{ // t == nums[mid] : 찾은 경우
                idx = mid;
                return;
            }
        }
        else{ // 경우2: 피벗 o (피벗이 껴 있는 경우)
            // nums[l] > nums[r] : 피벗이 낀 경우
            int mid = (l+r)/2;
            if(t==nums[l]) { idx=l; return; }
            if(t==nums[r]) { idx=r; return; }
            if(t==nums[mid]) { idx=mid; return; }
            
            BinarySearch(nums, l+1, mid-1, t);
            BinarySearch(nums, mid+1, r, t);
        }
    }
    
    int search(vector<int>& nums, int target) {
        BinarySearch(nums, 0, nums.size()-1, target);
        return idx;
    }
};

이 문제는 한 번에 해결하지 못하고,
두번정도 시행착오를 겪은 후 푼 문제입니다.

먼저 문제의 조건에서 "You must write an algorithm with O(log n) runtime complexity." 라고 있는데요,
여기서 저는 무조건 log n 때문에, 이진 탐색을 이용해야겠다고 생각했습니다.

그 뒤에는, 이진 탐색이 일어난 이후인데요
원래 이진탐색은 모든 데이터가 정렬이 되어있어야 가능합니다.
그런데 이 문제에서는 임의의 피벗값을 기준으로 데이터가 rotate 되어있어서, 원래의 알고있던 이진 탐색으로는 문제를 해결할 수 없습니다.

그게 이 문제의 출제의도라고 생각합니다.

일단, 경우를 두 개로 나눴습니다.

• 경우1: 피벗이 포함되지 않은 경우 (즉, 정렬이 잘 되어있는 리스트인 경우)

이 경우에는, 원래의 방법대로 이진 탐색을 진행하였습니다.

• 경우2: 피벗이 포함된 경우 (즉, 정렬이 중간에 한 번 바뀌는 경우)

이 경우에는, 양 끝 그리고 mid에 원하는 target이 있는지 검사 후,
이 경우에도 없으면 모든 경우에 대하여 탐색을 다시 진행하도록 알고리즘을 설계하였습니다.

이제 다른 풀이도 참고해보겠습니다.
discussion에서 가장 많은 표를 받은 풀이를 가져와봤습니다.

int beg=0,end=nums.size()-1,mid;
        while(beg<=end)
        {
            mid=(beg+end)/2;
            if(nums[mid]==target)
                return mid;
            if(nums[beg]<=nums[mid])
            {
                if(target<=nums[mid] && target>=nums[beg])
                    end=mid-1;
                else
                    beg=mid+1;
            }
            
            else
            {
                if(target>=nums[mid] && target<=nums[end])
                   beg=mid+1;
                else
                    end=mid-1;
            }
            
        }
        return -1;
    }

해당풀이링크