[백준/C++]15649, 15650, 15651, 15652번_ N과 M (1~4)

백준 N과 M 문제 총 12개를 4개씩 3번 나누어서
글을 작성해보도록 하겠습니다.
일단 가장 좋아하는 DFS, 재귀관련 부분입니다.
어렵지도 않아 딱히 풀이 설명도 필요없을 것 같구요.
각 문제들 마다 조금씩 차별점이나 포인트정도만 잡고 넘어가겠습니다.

저는 DFS 거의 재귀를 이용해서 다 풀었습니다.

먼저 첫 번째 문제는 다음과 같습니다.

1. N과 M (1)

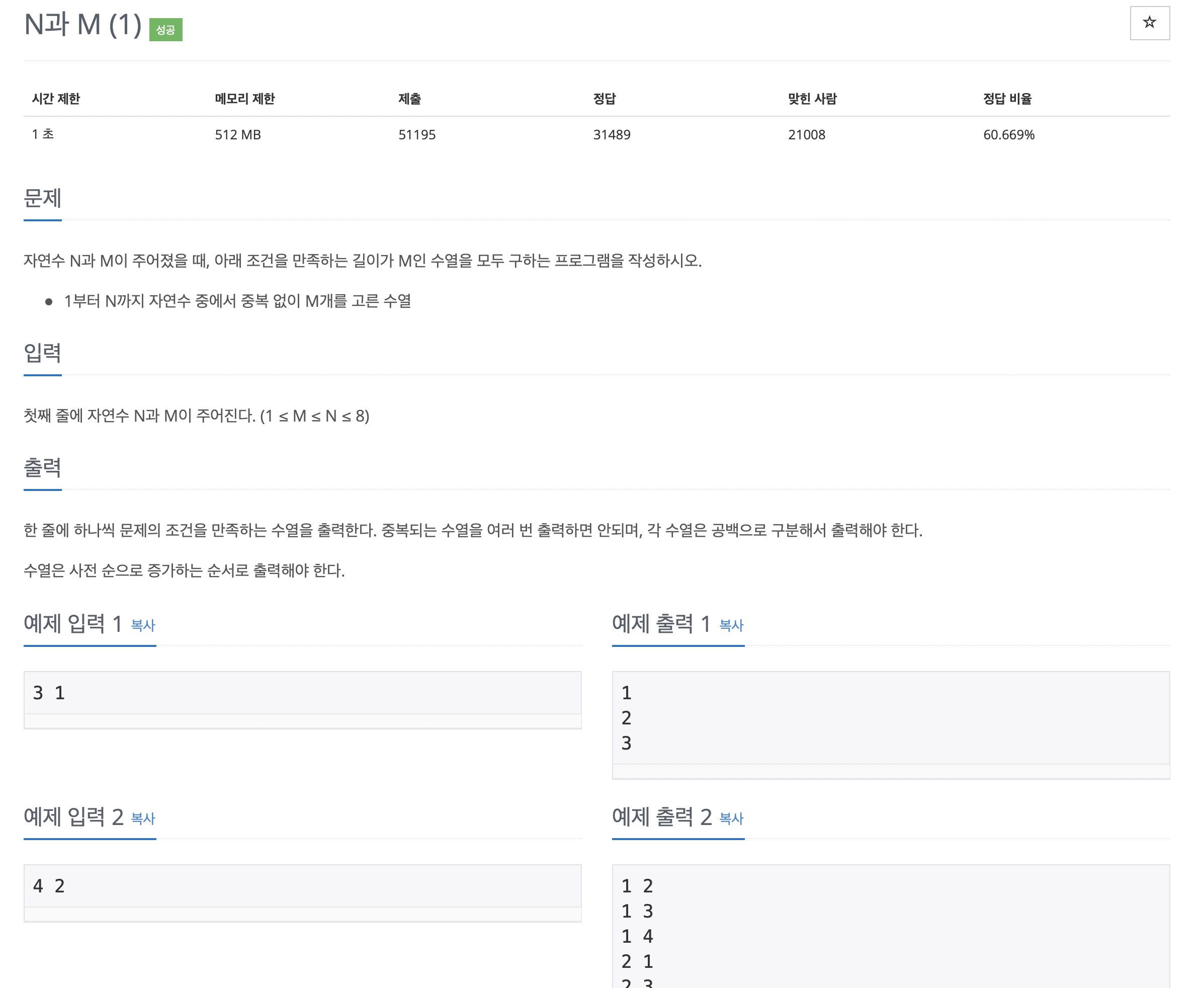
#include <bits/stdc++.h>
using namespace std;

int n, m;
int ch[9]={0, }; // 중복 여부 확인 배열
int res[9]={0, }; // 결과 배열

void DFS(int idx){
  if(idx==m+1){
    for(int i=1; i<=m; i++) cout<<res[i]<<" ";
    cout<<"\n";
  }
  else{
    for(int i=1; i<=n; i++){
      if(!ch[i]){
        ch[i]=1;
        res[idx]=i;
        DFS(idx+1);
        ch[i]=0;
      }
    }
  }
}

int main() {
    ios_base::sync_with_stdio(false);
    cin.tie(nullptr);

    cin>>n>>m;
    DFS(1);

    return 0;
}

---

2. N과 M (2)

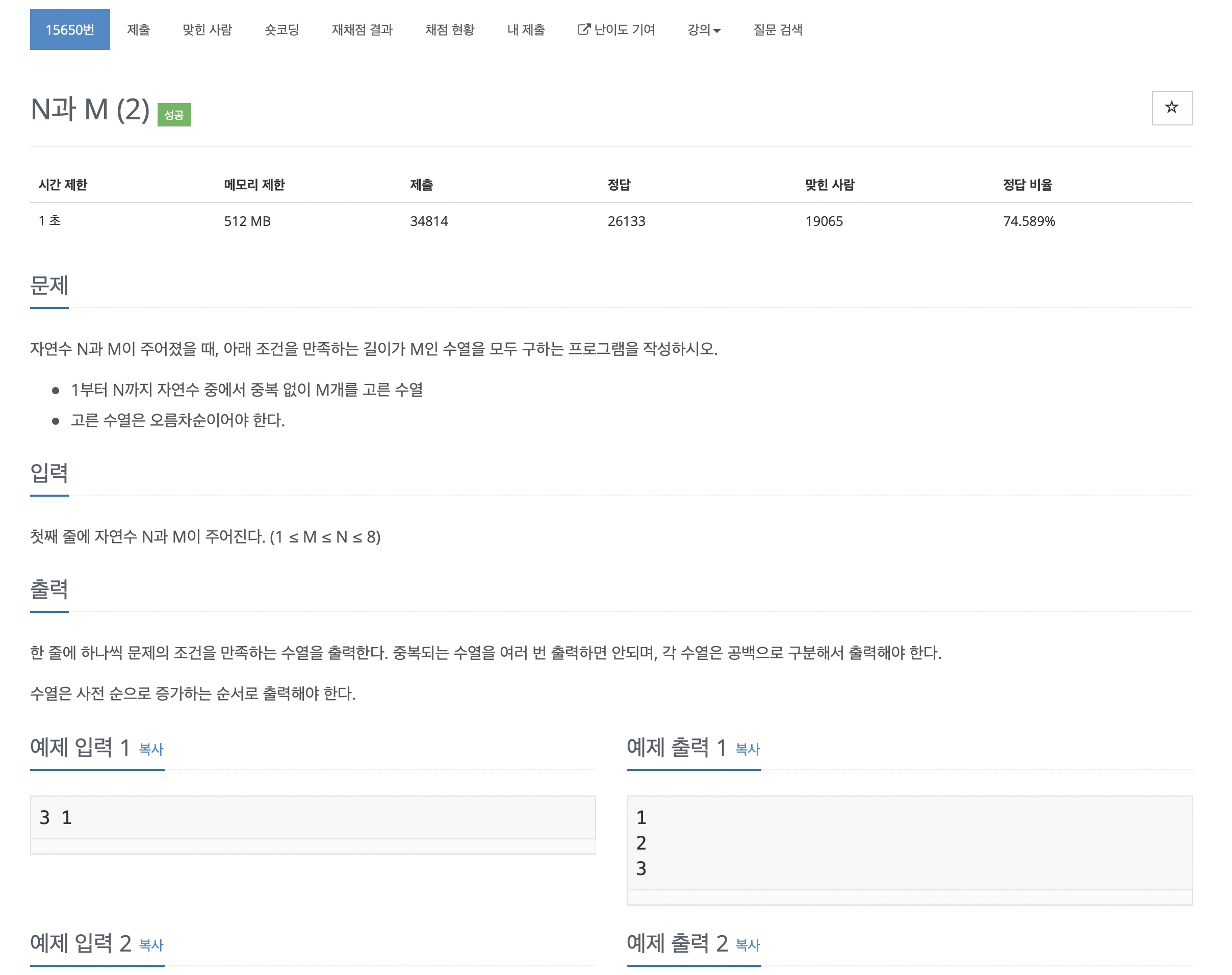
코드는 다음과 같습니다.

#include <bits/stdc++.h>
using namespace std;

int n, m;
int ch[9]={0, }; // 중복 여부 확인 배열
int res[9]={0, }; // 결과 배열

void DFS(int idx){
  if(idx==m+1){
    for(int i=1; i<=m; i++) cout<<res[i]<<" ";
    cout<<"\n";
  }
  else{
    for(int i=idx; i<=n; i++){ // i는 idx부터 시작
        if(res[idx-1]<i){ // 오름차순 조건
            res[idx]=i;
            DFS(idx+1);
        }
    }
  }
}

int main() {
    ios_base::sync_with_stdio(false);
    cin.tie(nullptr);

    cin>>n>>m;
    DFS(1);

    return 0;
}

앞 문제와의 차별점은 다음 수열은 "오름차순"인 수열만 출력해야한다는 점입니다.
그래서 저는 결과를 담는 배열 res를 1부터 시작을 했고, 인덱스 0에는 초기화 세팅에서 0으로 해주었습니다.

따라서 for문에서 i의 시작은 idx가 되고,
오름차순 조건은 i가 res[idx-1] 보다 커야합니다.

위와 같은 풀이의 시간복잡도는 O(n!)입니다.

위 문제는 또 다른 풀이로도 풀 수 있는데요,
풀이는 다음과 같습니다.

#include <bits/stdc++.h>
using namespace std;

int n, m;
int ch[9]={0, }; // 중복 여부 확인 배열
int res[9]={0, }; // 결과 배열

void DFS(int idx, int cnt){
  if(cnt==m){
    for(int i=1; i<=n; i++){
      if(ch[i]) cout<<i<<" ";
    }
    cout<<"\n";
  }
  else if(idx>n) return; // 재귀 탈출 조건2
  else{
    ch[idx]=1;
    DFS(idx+1, cnt+1);
    ch[idx]=0;
    DFS(idx+1, cnt);
  }
}

int main() {
    ios_base::sync_with_stdio(false);
    cin.tie(nullptr);

    cin>>n>>m;
    DFS(1, 0);

    return 0;
}

이는 시간복잡도가 O(2^n)의 풀이로,
앞에서 O(n!)의 풀이보다 조금 더 시간복잡도가 좋은 풀이입니다.
(함수 DFS에서 반복문만 잘 보면 시간복잡도를 바로 확인해볼 수 있습니다.)

---

3. N과 M (3)

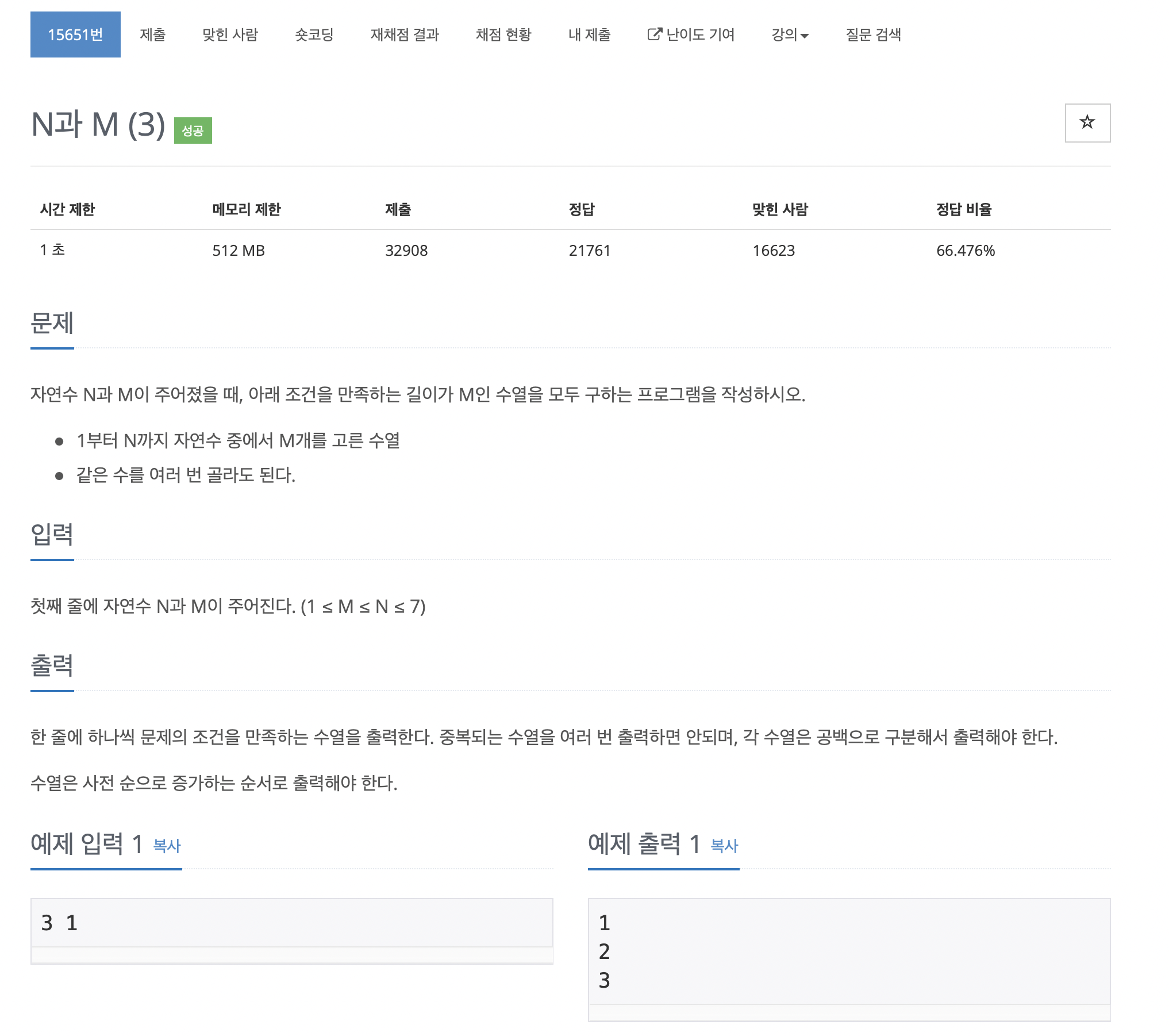
제 풀이는 다음과 같습니다.

#include <bits/stdc++.h>
using namespace std;

int n, m;
int ch[9]={0, }; // 중복 여부 확인 배열
int res[9]={0, }; // 결과 배열

void DFS(int idx){
  if(idx==m+1){
    for(int i=1; i<=m; i++){
      cout<<res[i]<<" ";
    }
    cout<<"\n";
  }
  else{
    for(int i=1; i<=n; i++){
      res[idx]=i;
      DFS(idx+1);
    }
  }
}

int main() {
    ios_base::sync_with_stdio(false);
    cin.tie(nullptr);

    cin>>n>>m;
    DFS(1);

    return 0;
}

이 문제가 거의 아무 조건도 없는,
제일 쉬운 문제인 것 같습니다.

---

4. N과 M (4)

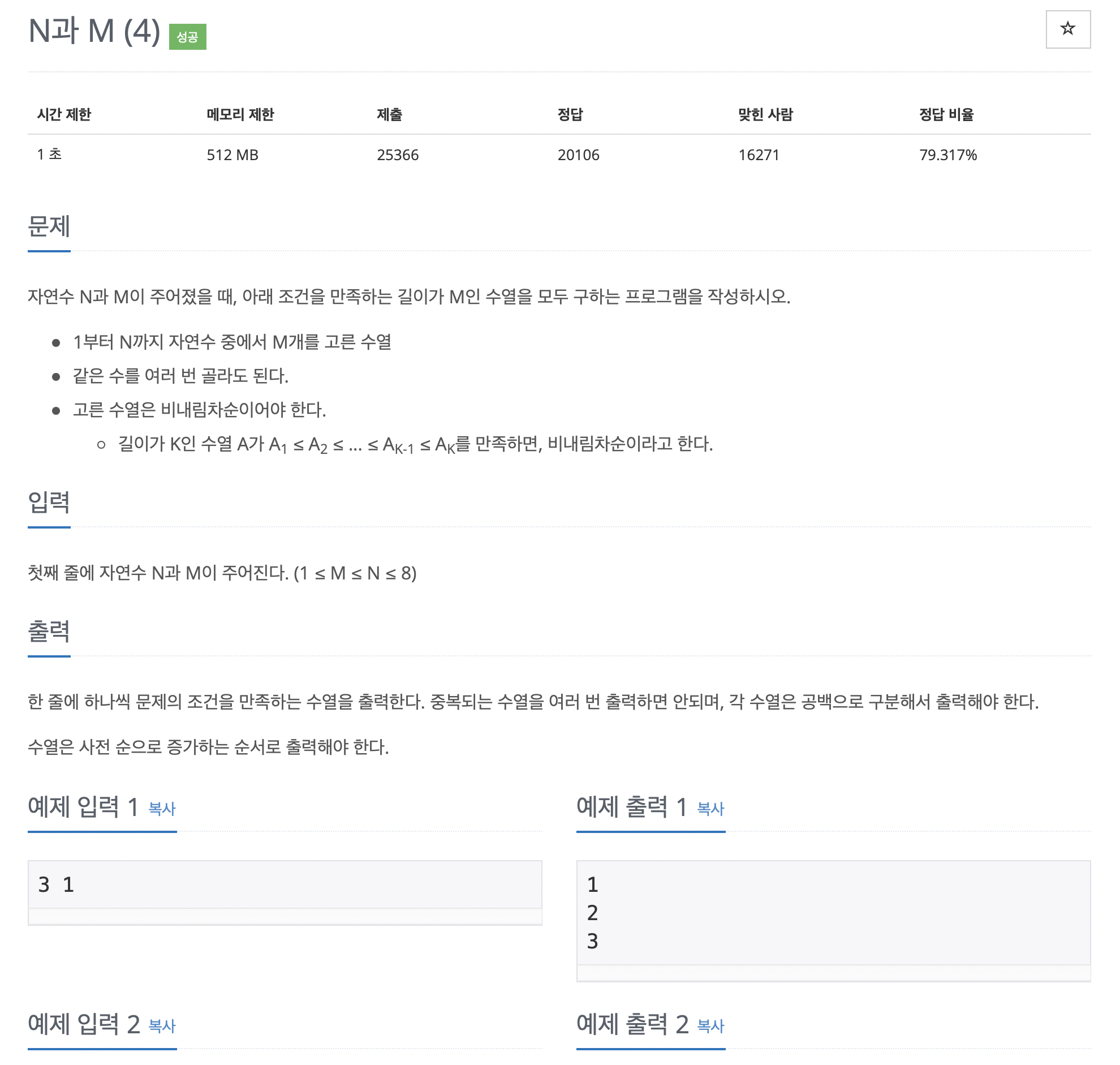
제 풀이는 다음과 같습니다.

#include <bits/stdc++.h>
using namespace std;

int n, m;
int ch[9]={0, }; // 중복 여부 확인 배열
int res[9]={0, }; // 결과 배열

void DFS(int idx){
  if(idx==m+1){
    for(int i=1; i<=m; i++) cout<<res[i]<<" ";
    cout<<"\n";
  }
  else{
    for(int i=1; i<=n; i++){
        if(res[idx-1]<=i){ // 오름차순 조건
            res[idx]=i;
            DFS(idx+1);
        }
    }
  }
}

int main() {
    ios_base::sync_with_stdio(false);
    cin.tie(nullptr);

    cin>>n>>m;
    DFS(1);

    return 0;
}

N과 M (2)의 문제와 거의 같고,
조건에서 수의 중복이 추가로 허용되므로,
res[idx-1] < i에서 res[idx-1]<=i 로만 변경하면 됩니다.