[백준/C++]1261번_ 알고스팟

문제는 다음과 같습니다.

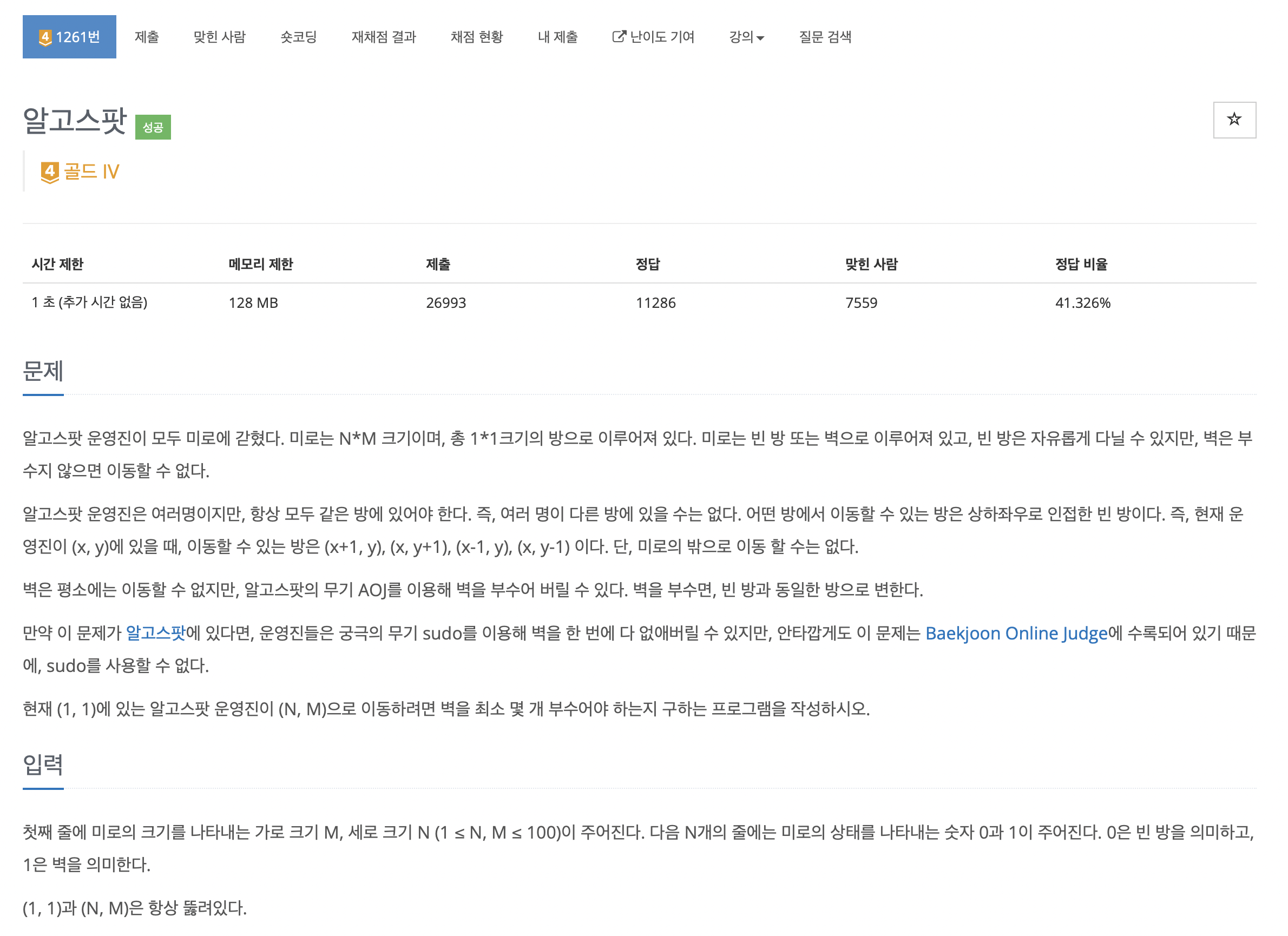
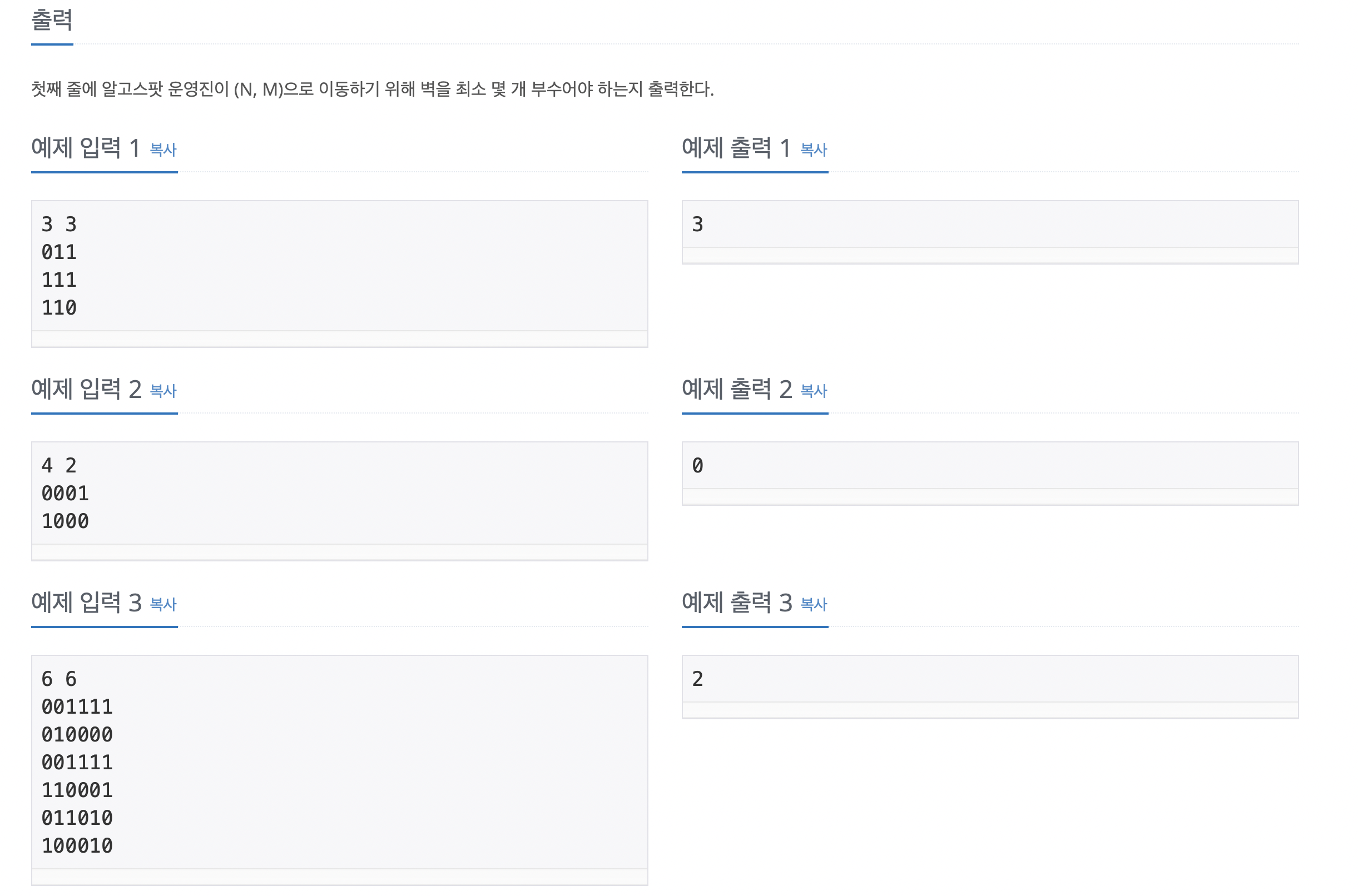
이 문제는 최단경로 문제 중 다익스트라 알고리즘으로 쉽게 해결할 수 있습니다.
그런데 다익스트라로 접근해야지 라고 생각하기까지가 어려운 것 같습니다.

저는 처음엔 dfs와 bfs를 섞어서 풀다가 엄청난 삽질을 했었고, 접근 방식이 틀렸다는것을 알고
다익스트라를 이용하라는 힌트를 받고 풀게 되었습니다.

작년 자료구조 수업 이후 오랜만에 본 다익스트라 ,,
하지만 그냥 까먹고 있었습니다 ㅠㅠ 악
다익스트라가 뭐였지? 하고 찾아보고 바로 딱 생각났고 그리고 아 이거로 풀면 바로 해결되겠구나!!! 생각을 했습니다.

이 문제에서 가중치는

• 벽을 부숴야 하는 경우 : 가중치 1
• 벽이 없는 경우 : 가중치 0

으로 생각하고, 다익스트라로 접근하면 됩니다.☺️

다익스트라 알고리즘을 이용하면 쉽게 풀 수 있기에,
전체 코드만 제시하겠습니다. 전체 코드는 다음과 같습니다.

#include <bits/stdc++.h>
using namespace std;

int n, m;
int a[102][102]={0, }; int d[102][102]={0, };

int main() {
  ios_base::sync_with_stdio(false);
  cin.tie(nullptr);
  queue<pair<int, int>> q; int dx[4]={0, 1, 0, -1}; int dy[4]={1, 0, -1, 0};
  
  cin>>m>>n;
  for(int i=1; i<=n; i++){
    string str; cin>>str;
    for(int j=0; j<str.size(); j++){
      a[i][j+1]=str[j]-'0';
      d[i][j+1]=INT_MAX;
    }
  }
  d[1][1]=0; q.push({1, 1});
  
  // 다익스트라 시작
  while(!q.empty()){
    int x = q.front().first; int y = q.front().second; int dis = d[x][y];
    q.pop();

    for(int i=0; i<4; i++){
      int sx = x+dx[i]; int sy = y+dy[i];
      if(sx>=1 && sx<=n && sy>=1 && sy<=m){
        if(a[sx][sy]==1){
          if(d[x][y]+1 < d[sx][sy]){
            d[sx][sy]=d[x][y]+1; // 원래보다 작다면 갱신하기
            q.push({sx, sy});
          }
        }
        else{ // a[sx][sy]==0 인 경우
          if(d[x][y] < d[sx][sy]){
            d[sx][sy]=d[x][y];
            q.push({sx, sy});
          }
        }
      }
    }
  }

  cout<<d[n][m]<<endl;
  return 0;
}

다익스트라 알고리즘

• 특정한 하나의 정점에서 다른 모든 정점으로 가는 최단경로를 알려줍니다.
• 간선의 가중치가 음수가 아닐 때에 적용할 수 있습니다.
• 따라서 현실세계에서 적용하기 좋은 알고리즘입니다.

✅ 가중치가 없는 그래프의 최단거리 문제는 대부분 BFS로 해결할 수 있습니다. 하지만, 간선에 가중치가 존재한다면 BFS가 아닌 최단거리 알고리즘을 통해 접근해야 합니다.

일반적인 가중치 그래프의 최단거리 문제 유형

1. 두 정점 간의 최단 거리를 구하는 문제 - 다익스트라
2. 하나의 정점에서 다른 모든 정점과의 최단거리를 구하는 문제 - 다익스트라
3. 하나의 정점으로 가는 모든 최단 경로를 구하는 문제
4. 정점 간의 모든 최단 경로를 구하는 문제