
문제는 다음과 같습니다.
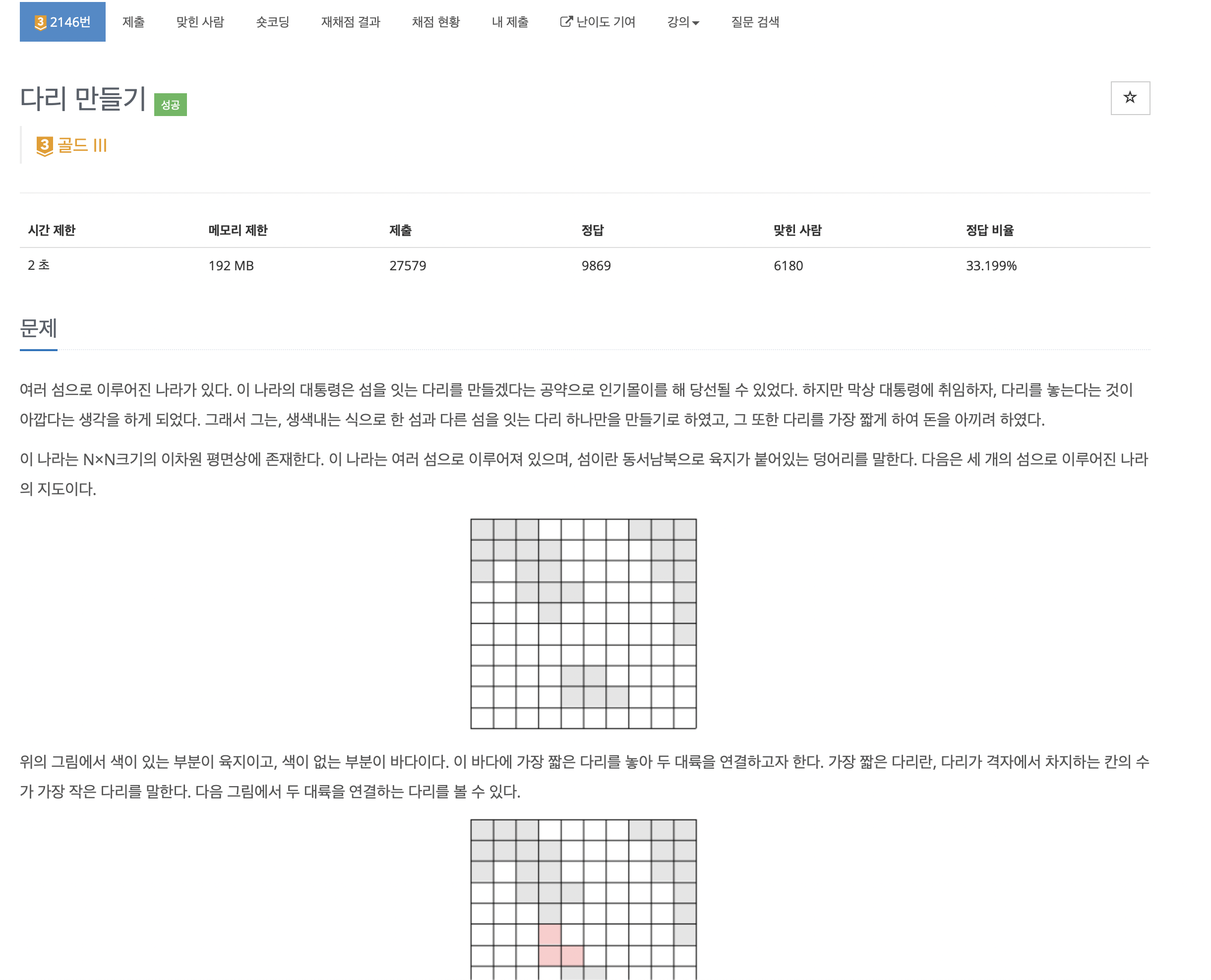
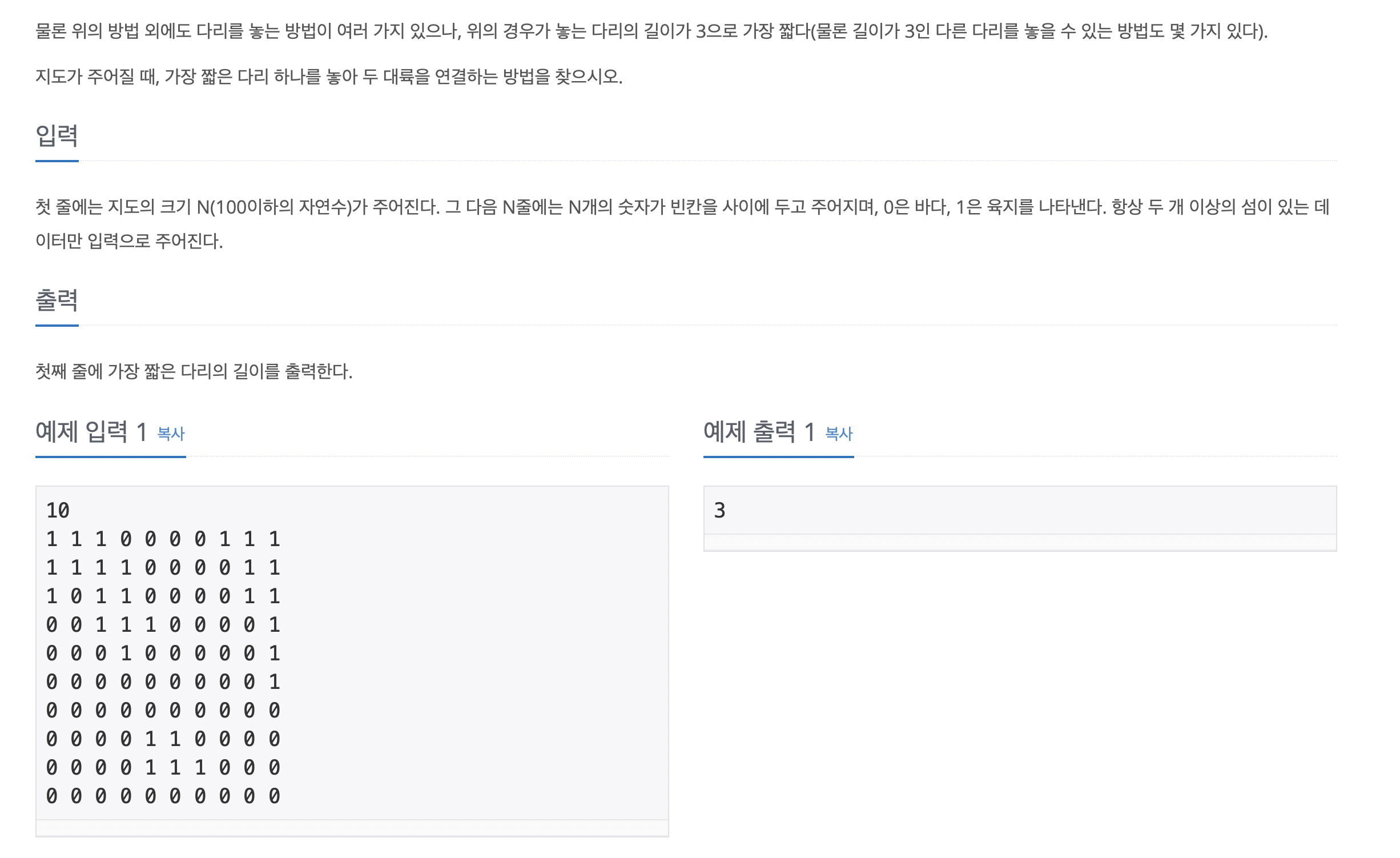
무려 이 문제 푸는데 이틀이나 걸렸다..
악 진짜 의지의 k-한국인 ..
(낼 수 있는 에러 다 내본듯;;)
먼저 이 문제를 푸는 과정은 두 단계로 나눠지고,
첫번째 단계에서는 DFS가 수행되고,
두번째 단계에서는 BFS가 수행됩니다.
말그대로 DFS와 BFS를 모두 공부할 수 있는 좋은 문제라는 것﹒﹒
과정1 : DFS를 수행하여, 각 섬들을 구별시킨다.
예를 들면,
1 1 0 0 1
1 1 0 0 1
0 0 0 0 0
1 1 0 1 1
1 1 1 0 1
의 분포를 가진 나라가 있다고 하면
여기서 DFS를 수행하여 섬을 구분지으면 다음과 같이 됩니다.
1 1 0 0 2
1 1 0 0 2
0 0 0 0 0
3 3 0 4 4
3 3 3 0 4
저는 숫자로 각 섬을 구분짓는 동시에 섬의 개수를 측정하였습니다.
dfs를 수행하여 각 섬을 구분짓는 코드는 다음과 같습니다.
int color = 1;
for(int i=1; i<=n; i++){
for(int j=1; j<=n; j++){
if(ch[i][j]==0 && a[i][j]){
ch[i][j] = color;
DFS(i, j, color);
color++;
}
}
} // 섬마다 구획나누기
// 실제 dfs가 수행되는 dfs 함수
void DFS(int t1, int t2, int col){
if(t1+1<=n && a[t1+1][t2]==1 && ch[t1+1][t2]==0){
ch[t1+1][t2]=col; DFS(t1+1, t2, col);
}
if(t2+1<=n && a[t1][t2+1]==1 && ch[t1][t2+1]==0){
ch[t1][t2+1]=col; DFS(t1, t2+1, col);
}
if(t1-1>=1 && a[t1-1][t2]==1 && ch[t1-1][t2]==0){
ch[t1-1][t2]=col; DFS(t1-1, t2, col);
}
if(t2-1>=1 && a[t1][t2-1]==1 && ch[t1][t2-1]==0){
ch[t1][t2-1]=col; DFS(t1, t2-1, col);
}
}과정2 : 섬과 섬 사이의 최단거리 구하기🔥
처음에 생각한 건 이 섬들을 모두 큐에 넣은 후에 한 번의 bfs로 이 섬들 간의 거리를 구하려고 했습니다.
하지만 계속해서 틀렸었고, 틀린 이유는 계속해서 예외가 발생하였습니다.
📌결국 생각한 건, 각각의 섬들에서 bfs를 수행하는 것이었습니다.📌
제한시간을 2초까지 준 것도 이 때문이 아닐까 싶네요
각 섬들에서 bfs를 수행하여 최단 거리를 벡터에 저장하여, 벡터에서 가장 작은 값을 반환하도록 하여 가장 짧은 다리를 구하였습니다.
각각의 섬들에서 bfs를 수행하는 코드는 다음과 같습니다.
// bfs 시작
vector<int> res;
for(int i=1; i<color; i++){
int d[101][101]={0, };
queue<pair<pair<int, int>, int>> q; int col = i;
for(int i=1; i<=n; i++){
for(int j=1; j<=n; j++){
if(ch[i][j]==col){
d[i][j]=1; q.push({{i, j}, 0});
}
}
}
while(!q.empty()){
int x = q.front().first.first; int y = q.front().first.second; int dis = q.front().second; q.pop();
if(ch[x][y]!=0 && ch[x][y]!=col){ res.push_back(dis-1); break; }
if(x+1<=n && d[x+1][y]==0) { d[x+1][y]=1; q.push({{x+1, y}, dis+1}); }
if(y+1<=n && d[x][y+1]==0) { d[x][y+1]=1; q.push({{x, y+1}, dis+1}); }
if(x-1>=1 && d[x-1][y]==0) { d[x-1][y]=1; q.push({{x-1, y}, dis+1}); }
if(y-1>=1 && d[x][y-1]==0) { d[x][y-1]=1; q.push({{x, y-1}, dis+1}); }
}
}
sort(res.begin(), res.end());
cout<<res[0]<<endl;전체 코드는 다음과 같습니다.
#include <bits/stdc++.h>
using namespace std;
int a[101][101]={0, }; int ch[101][101]={0, }; int n;
void DFS(int t1, int t2, int col){
if(t1+1<=n && a[t1+1][t2]==1 && ch[t1+1][t2]==0){
ch[t1+1][t2]=col; DFS(t1+1, t2, col);
}
if(t2+1<=n && a[t1][t2+1]==1 && ch[t1][t2+1]==0){
ch[t1][t2+1]=col; DFS(t1, t2+1, col);
}
if(t1-1>=1 && a[t1-1][t2]==1 && ch[t1-1][t2]==0){
ch[t1-1][t2]=col; DFS(t1-1, t2, col);
}
if(t2-1>=1 && a[t1][t2-1]==1 && ch[t1][t2-1]==0){
ch[t1][t2-1]=col; DFS(t1, t2-1, col);
}
}
int main() {
ios_base::sync_with_stdio(false);
cin.tie(nullptr);
cin>>n;
for(int i=1; i<=n; i++){
for(int j=1; j<=n; j++){
cin>>a[i][j];
}
}
int color = 1;
for(int i=1; i<=n; i++){
for(int j=1; j<=n; j++){
if(ch[i][j]==0 && a[i][j]){
ch[i][j] = color;
DFS(i, j, color);
color++;
}
}
} // 섬마다 구획나누기
// bfs 시작
vector<int> res;
for(int i=1; i<color; i++){
int d[101][101]={0, };
queue<pair<pair<int, int>, int>> q; int col = i;
for(int i=1; i<=n; i++){
for(int j=1; j<=n; j++){
if(ch[i][j]==col){
d[i][j]=1; q.push({{i, j}, 0});
}
}
}
while(!q.empty()){
int x = q.front().first.first; int y = q.front().first.second; int dis = q.front().second; q.pop();
if(ch[x][y]!=0 && ch[x][y]!=col){ res.push_back(dis-1); break; }
if(x+1<=n && d[x+1][y]==0) { d[x+1][y]=1; q.push({{x+1, y}, dis+1}); }
if(y+1<=n && d[x][y+1]==0) { d[x][y+1]=1; q.push({{x, y+1}, dis+1}); }
if(x-1>=1 && d[x-1][y]==0) { d[x-1][y]=1; q.push({{x-1, y}, dis+1}); }
if(y-1>=1 && d[x][y-1]==0) { d[x][y-1]=1; q.push({{x, y-1}, dis+1}); }
}
}
sort(res.begin(), res.end());
cout<<res[0]<<endl;
return 0;
}추가)
마지막에서 섬에서 섬까지 다리를 놓을 때,
저는 모든 섬에서 다른 섬까지의 bfs를 구해서 이를 해결했는데,
한 번의 bfs 수행으로만 이를 구할 수 있더라구요!
(난 했었는데 .. 실패했는데)
아무튼 엄청난 시간복잡도의 개선이 이루어질 수 있는 풀이라
공부하고 넘어가면 너무 좋을 것 같아 가져왔어요
풀이의 핵심은 다음과 같습니다.
- 모든 섬을 queue에 넣습니다.
- 섬에서 거리를 넓혀갈 때, 거리 뿐만 아니라 어디에서 뻗어나온 섬인지를 기록합니다 -> (저는 ch배열을 재사용했습니다.)
즉 이렇게 1번만 bfs를 수행합니다.
그리고 다시 이차원 배열의 모든 점들에 대해서 다음을 검토합니다.
한 점에서 그에 이웃한 네 점을 살펴보는 데,
❗️출신 섬이 다를 경우 -> 다리를 놓을 수 있다❗️ 는 점을 이용합니다.
또한 이 때의 다리가 격자에서 차지하는 칸은 이 이웃한 두 칸의 거리의 합과 같습니다.
이를 이용한 개선된 전체 코드는 다음과 같습니다.
(마지막 bfs 수행되는 부분이 개선되었습니다.)
#include <bits/stdc++.h>
using namespace std;
int a[101][101]={0, }; int ch[101][101]={0, }; int n;
void DFS(int t1, int t2, int col){
if(t1+1<=n && a[t1+1][t2]==1 && ch[t1+1][t2]==0){
ch[t1+1][t2]=col; DFS(t1+1, t2, col);
}
if(t2+1<=n && a[t1][t2+1]==1 && ch[t1][t2+1]==0){
ch[t1][t2+1]=col; DFS(t1, t2+1, col);
}
if(t1-1>=1 && a[t1-1][t2]==1 && ch[t1-1][t2]==0){
ch[t1-1][t2]=col; DFS(t1-1, t2, col);
}
if(t2-1>=1 && a[t1][t2-1]==1 && ch[t1][t2-1]==0){
ch[t1][t2-1]=col; DFS(t1, t2-1, col);
}
}
int main() {
ios_base::sync_with_stdio(false);
cin.tie(nullptr);
cin>>n;
for(int i=1; i<=n; i++){
for(int j=1; j<=n; j++){
cin>>a[i][j];
}
}
int color = 1;
for(int i=1; i<=n; i++){
for(int j=1; j<=n; j++){
if(ch[i][j]==0 && a[i][j]){
ch[i][j] = color;
DFS(i, j, color);
color++;
}
}
} // 섬마다 구획나누기
// bfs 시작
int d[101][101]; memset(d, -1, sizeof(d)); // d 배열: 거리 배열이자 체크 배열
queue<pair<int, int>> q;
for(int i=1; i<=n; i++){
for(int j=1; j<=n; j++){
if(ch[i][j]!=0){ // 모든 섬들에 대해서
d[i][j]=0; q.push({i, j});
}
}
}
while(!q.empty()){
int x = q.front().first; int y = q.front().second; q.pop();
if(x+1<=n && d[x+1][y]==-1) { ch[x+1][y]=ch[x][y]; d[x+1][y]=d[x][y]+1; q.push({x+1, y}); }
if(y+1<=n && d[x][y+1]==-1) { ch[x][y+1]=ch[x][y]; d[x][y+1]=d[x][y]+1; q.push({x, y+1}); }
if(x-1>=1 && d[x-1][y]==-1) { ch[x-1][y]=ch[x][y]; d[x-1][y]=d[x][y]+1; q.push({x-1, y}); }
if(y-1>=1 && d[x][y-1]==-1) { ch[x][y-1]=ch[x][y]; d[x][y-1]=d[x][y]+1; q.push({x, y-1}); }
} // bfs 끝
int ans = 100000; int dx[4] = {-1, 0, 1, 0}; int dy[4] = {0, 1, 0, -1};
for(int i=1; i<=n; i++){
for(int j=1; j<=n; j++){
int dis = d[i][j]; int col = ch[i][j];
// 상, 하, 좌, 우 를 검토 시 서로 다른 섬이면 다리를 놓을 수 있음
for(int k=0; k<4; k++){
int x = i+dx[k]; int y = j+dy[k];
if(x>=1 && x<=n && y>=1 && y<=n && ch[x][y]!=col){
int tmp_dis = dis + d[x][y];
if(tmp_dis < ans) ans=tmp_dis;
}
}
}
}
cout<<ans<<endl;
return 0;
}그리고 한 점에서 그에 이웃한 네 점을 살펴볼 때,
int dx[4] = {-1, 0, 1, 0};
int dy[4] = { 0, 1, 0, -1};
을 이용해 한 번의 반복문을 돌리면 매우 쉽게 이웃한 점들을 살펴볼 수 있습니다.
각각을 if문으로 돌리는 것 보다 이렇게 깔끔하게 한 번의 for문으로 수행하는 것이 더 좋은 것 같습니다.😊

이렇게 시간복잡도가 개선된 것을 확인할 수 있습니다🥳🥳
