Evaluation Metrics for Regression

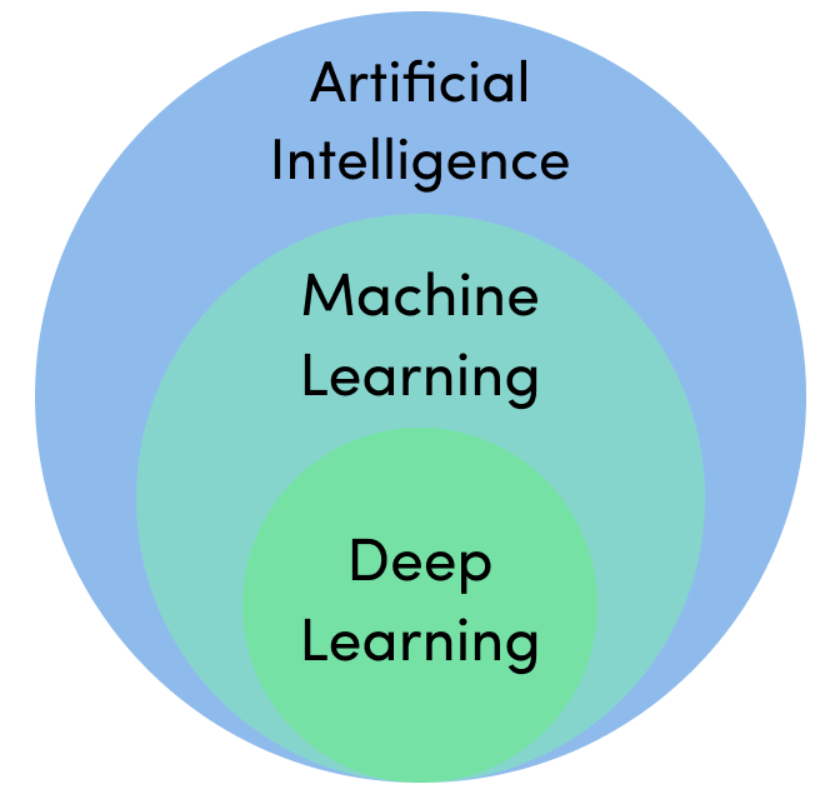
회귀모델 평가지표

1. MAE (Mean Absolute Error)

실제 값과 예측 값의 차이를 절댓값으로 변환해 평균한 것
MAE = $\frac{1}{n}\sum_{i=1}^{n}\left | y_{i} - \hat{y_{i}} \right |$

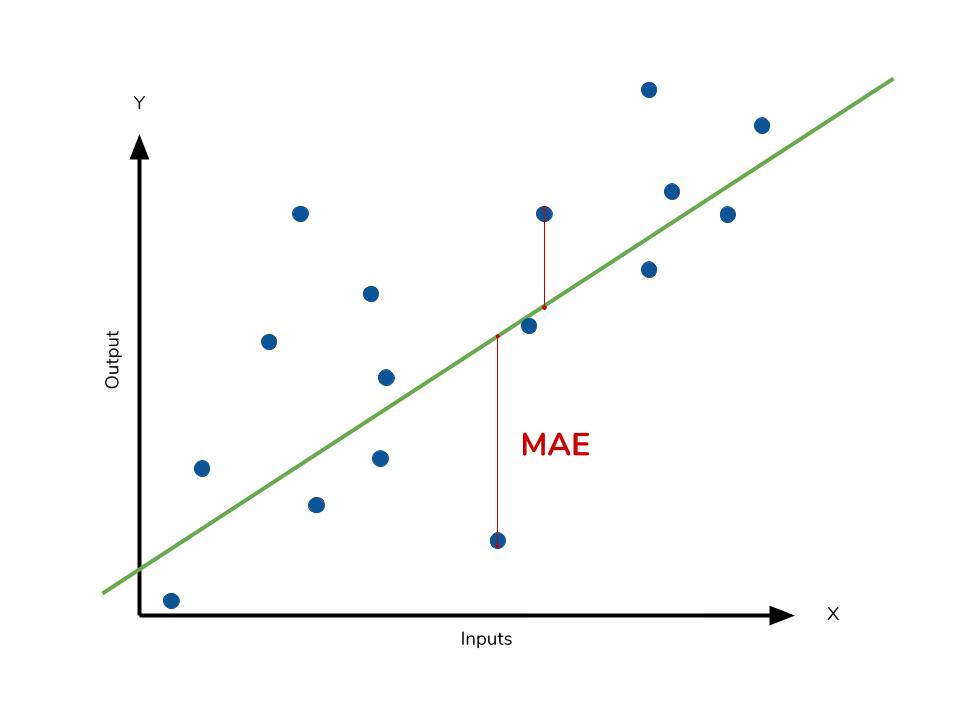
절대값을 취하기 때문에 모델이 underperformance 인지 overperformance 인지 알 수 없다

• underperformance: 모델이 실제보다 낮은 값으로 예측
• overperformance: 모델이 실제보다 높은 값으로 예측

from sklearn.metrics import mean_absolute_error
mean_absolute_error(y_test, y_pred)

※ Mae 값이 3이라면 평균적으로 3정도를 잘못 예측하는 것이다

---

2. MSE (Mean Squared Error)

실제 값과 예측 값의 차이를 제곱해 평균한 것
MSE = $\frac{1}{n}\sum_{i=1}^{n}(y_{i} - \hat{y_{i}})^{2}$

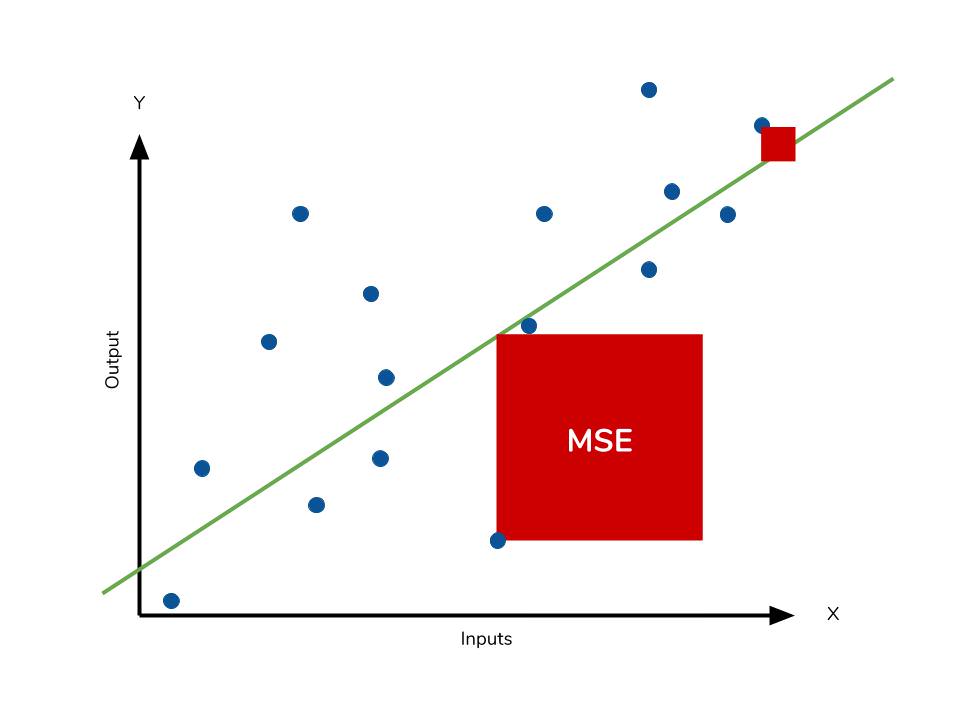
• 예측값과 실제값 차이의 면적의 합
• 특이값이 존재하면 수치가 많이 늘어난다

from sklearn.metrics import mean_squared_error
mean_squared_error(y_test, y_pred)

※ MSE 값이 4라면 평균적으로 2정도를 잘못 예측하는 것이다

---

3. RMSE (Root Mean Squared Error)

MSE에 루트를 씌운 값
RMSE = $\sqrt{MSE}$

• MSE 값은 오류의 제곱을 구하므로 실제 오류 평균보다 더 커지는 특성이 있어 MSE에 루트를 씌운 RMSE 값을 쓴다

• 에러에 제곱을 하기 때문에 에러가 크면 클수록 그에 따른 가중치가 높이 반영된다. 그러므로 예측 결과물의 에러가 10이 나온 것이 5로 나온 것보다, 정확히 $2^2$(4)배가 나쁜 도메인에서 쓰기 적합한 산식이다

• 에러에 따른 손실이 기하 급수적으로 올라가는 상황에서 쓰기 적합하다

---

4. $R^2$ (R-squared)

실제 관측값의 분산대비 예측값의 분산을 계산하여 데이터 예측의 정확도 성능을 측정하는 지표
$R^2 = 1 - \frac{SSE}{SST} = \frac {SSR}{SST}$

• 0~1까지 수로 나타내어지며 1에 가까울수록 좋은 모델

• SSE(Sum of Squares Error, 관측치와 예측치 차이): $\sum_{i=1}^{n}(y_{i} - \hat{y_{i}})^{2}$
• SSR(Sum of Squares due to Regression, 예측치와 평균 차이): $\sum_{i=1}^{n}(\hat{y_{i}} - \bar{y_{i}})^{2}$
• SST(Sum of Squares Total, 관측치와 평균 차이): $\sum_{i=1}^{n}(y_{i} - \bar{y_{i}})^{2}$ ,
  SSE + SSR

from sklearn.metrics import r2_score
r2_score(y_test, y_pred)