[알고리즘] 구간 합

구간 합

합 배열을 이용하여 시간 복잡도를 더 줄이기 위해 사용하는 특수한 목적의 알고리즘

구간 합의 핵심 이론

구간 합 알고리즘을 활용하려면 먼저 합 배열을 구해야 한다.
합 배열은 기존의 배열을 전처리한 배열이라 생각하면 된다. 이렇게 합 배열을 미리 구해놓으면 기존 배열의 일정 범위의 합을 구하는 시간 복잡도가 O(N)에서 O(1)로 감소한다.

• 합 배열 S 정의
  S[i] = A[0] + A[1] + A[2] + ... + A[i-1] + A[i]

• 합 배열 S를 만드는 공식
  S[i] = S[i-1] + A[i]

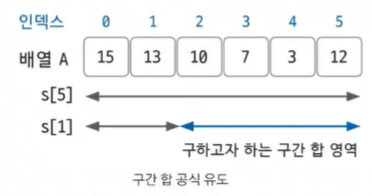
• 구간 합을 구하는 공식
  S[j] - S[i-1] -> i에서 j까지 구간 합
  

---

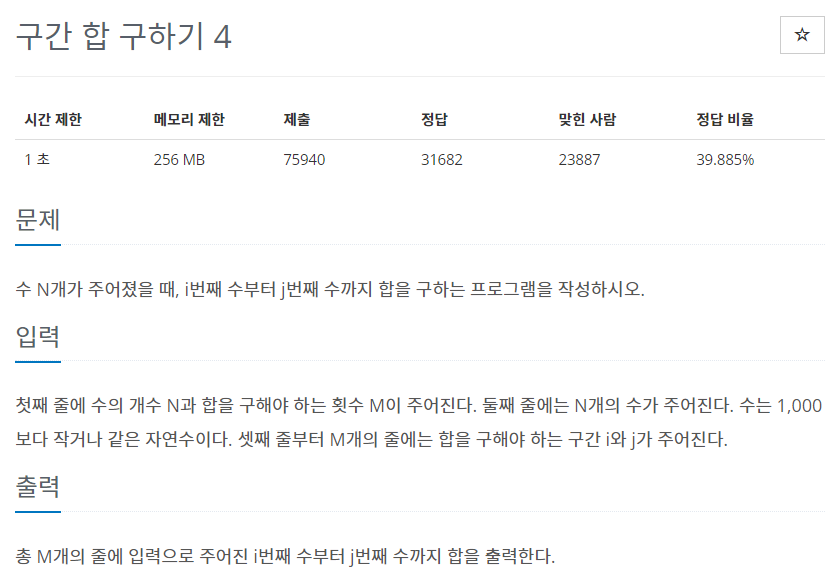
백준 11659번: 구간 합 구하기4

- 문제 분석하기

문제에서 수의 개수와, 합을 구해야 하는 횟수는 최대 100,000이다. 게다가 구간마다 합을 매번 계산하면 0.5초 안에 모든 구간 합 계산을 끝낼 수 없다. 이럴 때 바로 구간 합을 이용해야 한다. 구간 합 개념을 적용하는 가장 기본적인 문제이므로 핵심 이론에서 배웠던 내용을 그대로 적용해 코드를 작성하면 된다.

- 슈도코드 작성하기

suNo(숫자 개수), quizNo(질의 개수) 저장하기
for(숫자 개수만큼 반복하기) {
	합 배열 생성하기 S[i] = S[i-1] + A[i]
}
for(질의 개수만큼 반복하기){
	질의 범위 받기(i~j)
    구간 합 출력하기(S[j] - S[i-1]
}

- 제출 코드

받는 데이터가 많은 경우 Scanner보다 BufferedReader 사용하는게 더 빠르다.

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;

public class Baekjoon11659 {
	public static void main(String[] args) throws IOException{
		BufferedReader bufferedReader = new BufferedReader(new InputStreamReader(System.in));
		StringTokenizer stringTokenizer = new StringTokenizer(bufferedReader.readLine());
        
		int suNo = Integer.parseInt(stringTokenizer.nextToken());
		int quizNo = Integer.parseInt(stringTokenizer.nextToken());
		long[]S = new long[suNo + 1];
		
		stringTokenizer = new StringTokenizer(bufferedReader.readLine());
		for(int i = 1; i <= suNo; i++) {
			S[i] = S[i-1] + Integer.parseInt(stringTokenizer.nextToken());
		}
		
		for(int q = 0; q < quizNo; q++) {
			stringTokenizer = new StringTokenizer(bufferedReader.readLine());
			int i = Integer.parseInt(stringTokenizer.nextToken());
			int j = Integer.parseInt(stringTokenizer.nextToken());
            
			System.out.println(S[j] - S[i-1]);
		}
		
	}
}

---

reference

Do it! 알고리즘 코딩테스트 with JAVA