그래프 탐색 알고리즘
- 탐색(Search)이란 많은 양의 데이터 중에서 원하는 데이터를 찾는 과정
- 대표적인 그래프 탐색 알고리즘으로는 DFS와 BFS가 있다.
- DFS/BFS는 코딩 테스트에서 매우 자주 등장하는 유형이므로 반드시 숙지
⭐ Stack
Stack<Integer> s = new Stack<>();
import java.util.*;
public class Main {
public static void main(String[] args) {
Stack<Integer> s = new Stack<>();
// 삽입(5) - 삽입(2) - 삽입(3) - 삽입(7) - 삭제() - 삽입(1) - 삽입(4) - 삭제()
s.push(5);
s.push(2);
s.push(3);
s.push(7);
s.pop();
s.push(1);
s.push(4);
s.pop();
// 스택의 최상단 원소부터 출력
while (!s.empty()) {
System.out.println(s.peek());
s.pop();
}
}
}⭐ Queue
Queue<Integer> q = new LinkedList<>();
import java.util.*;
public class Main {
public static void main(String[] args) {
Queue<Integer> q = new LinkedList<>();
// 삽입(5) - 삽입(2) - 삽입(3) - 삽입(7) - 삭제() - 삽입(1) - 삽입(4) - 삭제()
q.offer(5);
q.offer(2);
q.offer(3);
q.offer(7);
q.poll();
q.offer(1);
q.offer(4);
q.poll();
// 먼저 들어온 원소부터 추출
while (!q.isEmpty()) {
System.out.println(q.poll());
}
}
}⭐ 재귀 함수
재귀 함수(Recursive Function)란 자기 자신을 다시 호출하는 함수
-
무한히 반복되는 재귀함수 예제
import java.util.*; public class Main { public static void recursiveFunction() { System.out.println("재귀 함수를 호출합니다."); recursiveFunction(); } public static void main(String[] args) { recursiveFunction(); } } -
재귀 함수의 종료 조건
- 재귀 함수를 문제 풀이에서 사용할 때는 재귀 함수의 종료 조건을 반드시 명시해야 한다.
- 종료 조건을 제대로 명시하지 않으면 함수가 무한히 호출될 수 있다.
- 종료 조건을 포함한 재귀함수 예제
import java.util.*; public class Main { public static void recursiveFunction(int i) { // 100번째 호출을 했을 때 종료되도록 종료 조건 명시 if (i == 100) return; System.out.println(i + "번째 재귀 함수에서 " + (i + 1) + "번째 재귀함수를 호출합니다."); recursiveFunction(i + 1); System.out.println(i + "번째 재귀 함수를 종료합니다."); } public static void main(String[] args) { recursiveFunction(1); } } -
재귀 함수 사용의 유의사항
- 재귀 함수를 잘 활용하면 복잡한 알고리즘을 간결하게 작성할 수 있다.
단, 오히려 다른 사람이 이해하기 어려운 형태의 코드가 될 수도 있으므로 신중하게 사용 - 모든 재귀 함수는 반복문을 이용하여 동일한 기능을 구현할 수 있다.
- 재귀 함수가 반복문보다 유리한 경우도 있고 불리한 경우도 있다.
- 컴퓨터가 함수를 연속적으로 호출하면 컴퓨터 메모리 내부의 스택 프레임에 쌓인다.
따라서 별도의 스택 자료형을 사용하지 않고도 재귀 함수를 통해 스택의 기능을 구현할 수 있다.
- 재귀 함수를 잘 활용하면 복잡한 알고리즘을 간결하게 작성할 수 있다.
📄 팩토리얼 구현 예제
- n! = 1 2 3 ... (n-1) * n
- 수학적으로 0!과 1!의 값은 1이다.
import java.util.*;
public class Main {
// 반복적으로 구현한 n!
public static int factorialIterative(int n) {
int result = 1;
// 1부터 n까지의 수를 차례대로 곱하기
for (int i = 1; i <= n; i++) {
result *= i;
}
return result;
}
// 재귀적으로 구현한 n!
public static int factorialRecursive(int n) {
// n이 1 이하인 경우 1을 반환
if (n <= 1) return 1;
// n! = n * (n - 1)!를 그대로 코드로 작성하기
return n * factorialRecursive(n - 1);
}
public static void main(String[] args) {
// 각각의 방식으로 구현한 n! 출력(n = 5)
System.out.println("반복적으로 구현:" + factorialIterative(5));
System.out.println("재귀적으로 구현:" + factorialRecursive(5));
}
}📄 최대공약수 계산(유클리드 호제법)
-
두 개의 자연수에 대한 최대공약수를 구하는 대표적인 알고리즘으로는 유클리드 호제법이 있다.
-
유클리드 호제법
- 두 자연수 A, B에 대하여 (A > B) A를 B로 나눈 나머지를 R이라고 하자.
- 이때 A와 B의 최대공약수는 B와 R의 최대공약수와 같다
-
유클리드 호제법의 아이디어를 그대로 재귀 함수로 작성할 수 있다.
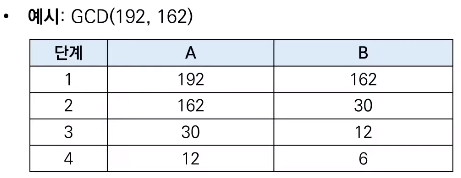
GCD(192, 162) = GCD(12, 6) = 6
public class Main {
public int gcd(int a, int b){
if (a % b == 0) return b;
else return gcd(b, a % b);
}
public static void main(String[] args) {
System.out.println(gcd(192, 162));
}
}⭐ DFS (Depth-First Search)
스택 자료구조 / 재귀 함수 이용
깊이 우선 탐색이라고 부르며 그래프에서 깊은 부분을 우선적으로 탐색하는 알고리즘
동작 과정
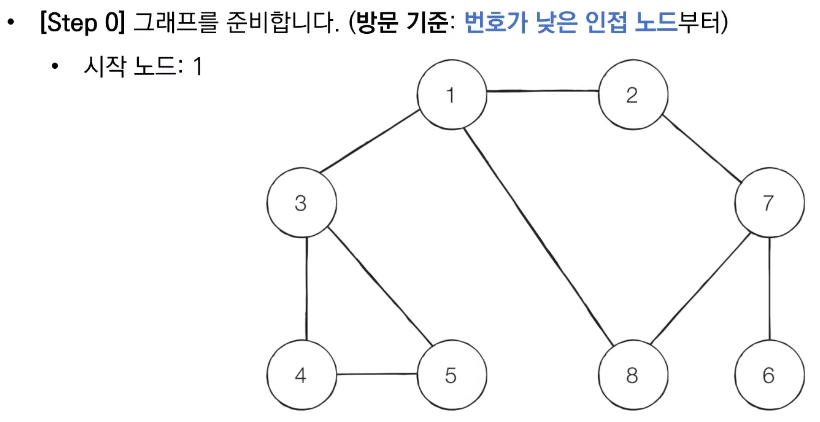
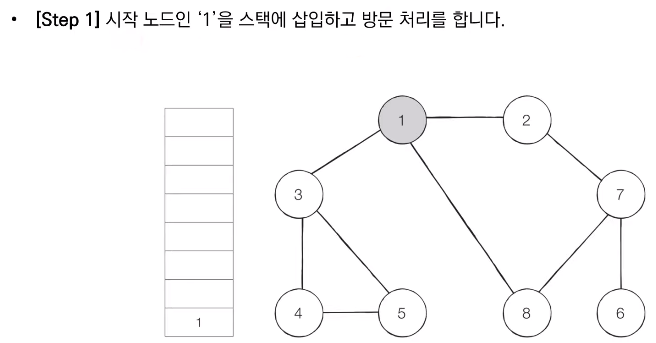
- 탐색 시작 노드를 스택에 삽입하고 방문 처리를 한다.
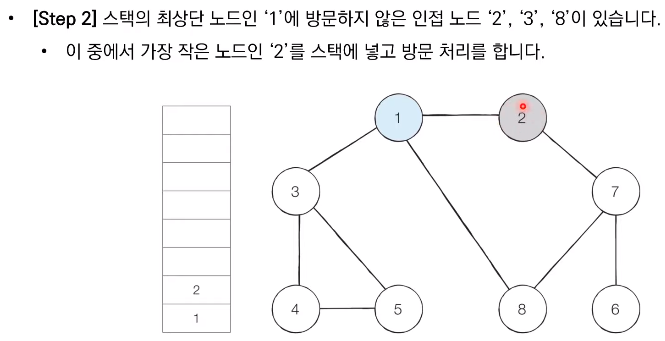
- 스택의 최상단 노드에 방문하지 않은 인접한 노드가 하나라도 있으면 그 노드를 스택에 넣고 방문 처리한다. 방문하지 않은 인접 노드가 없으면 스택에서 최상단 노드를 꺼낸다.
- 더 이상 2번의 과정을 수행할 수 없을 때까지 반복한다.
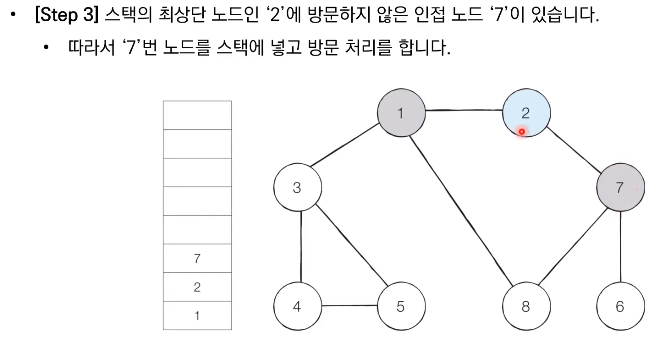
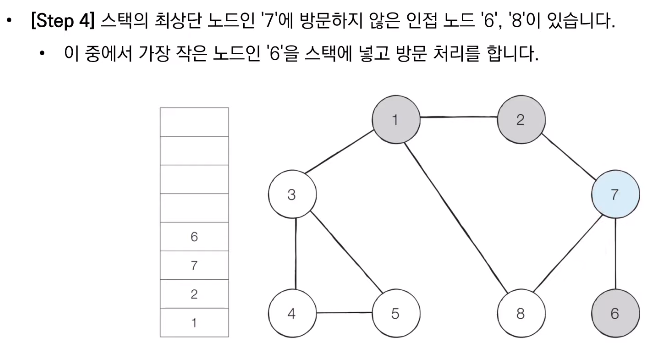
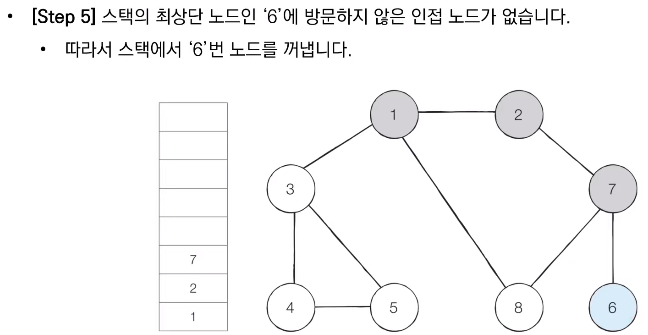
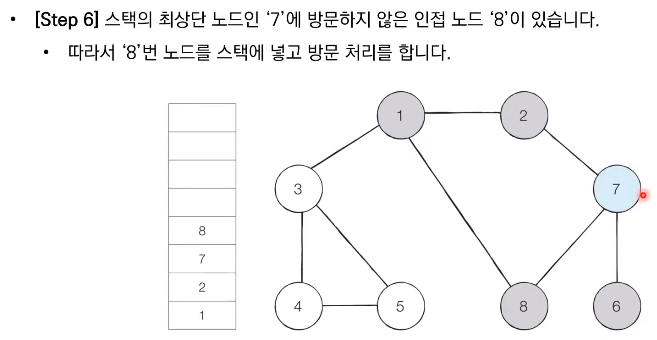
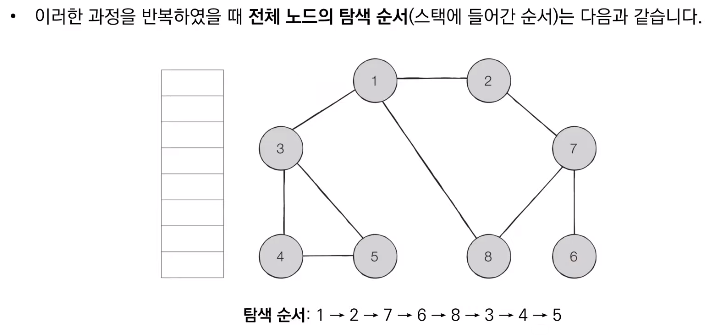
📝 코드 구현
import java.util.*;
public class Main {
public static boolean[] visited = new boolean[9];
public static ArrayList<ArrayList<Integer>> graph = new ArrayList<ArrayList<Integer>>();
// DFS 함수 정의
public static void dfs(int x) {
// 현재 노드를 방문 처리
visited[x] = true;
System.out.print(x + " ");
// 현재 노드와 연결된 다른 노드를 재귀적으로 방문
for (int i = 0; i < graph.get(x).size(); i++) {
int y = graph.get(x).get(i);
if (!visited[y]) dfs(y);
}
}
public static void main(String[] args) {
// 그래프 초기화
for (int i = 0; i < 9; i++) {
graph.add(new ArrayList<Integer>());
}
// 노드 1에 연결된 노드 정보 저장
graph.get(1).add(2);
graph.get(1).add(3);
graph.get(1).add(8);
// 노드 2에 연결된 노드 정보 저장
graph.get(2).add(1);
graph.get(2).add(7);
// 노드 3에 연결된 노드 정보 저장
graph.get(3).add(1);
graph.get(3).add(4);
graph.get(3).add(5);
// 노드 4에 연결된 노드 정보 저장
graph.get(4).add(3);
graph.get(4).add(5);
// 노드 5에 연결된 노드 정보 저장
graph.get(5).add(3);
graph.get(5).add(4);
// 노드 6에 연결된 노드 정보 저장
graph.get(6).add(7);
// 노드 7에 연결된 노드 정보 저장
graph.get(7).add(2);
graph.get(7).add(6);
graph.get(7).add(8);
// 노드 8에 연결된 노드 정보 저장
graph.get(8).add(1);
graph.get(8).add(7);
dfs(1);
}
}⭐ BFS (Breadth-First Search)
큐 자료구조 이용
너비 우선 탐색이라 부르며, 그래프에서 가까운 노드부터 우선적으로 탐색하는 알고리즘
동작 과정
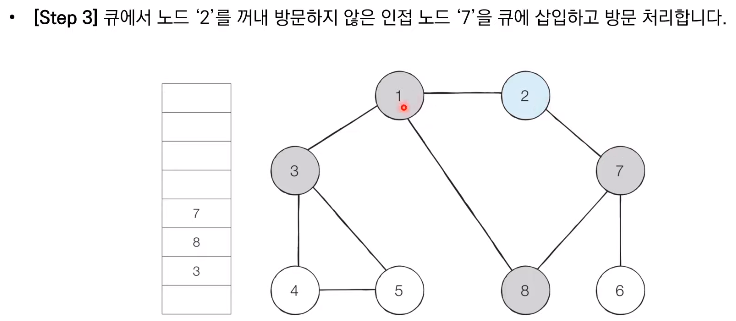
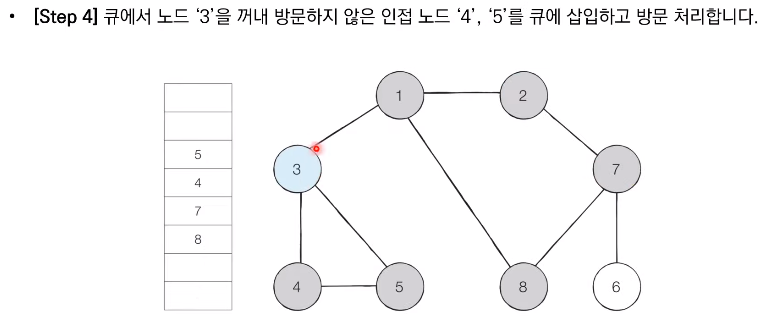
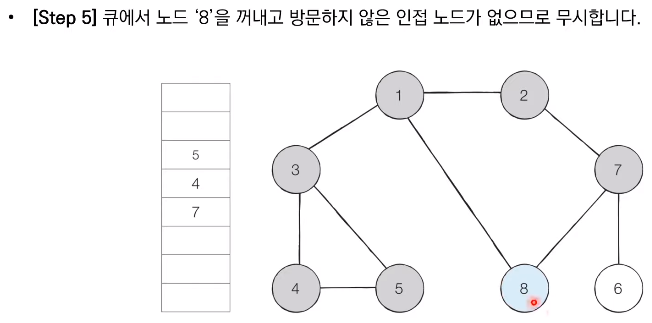
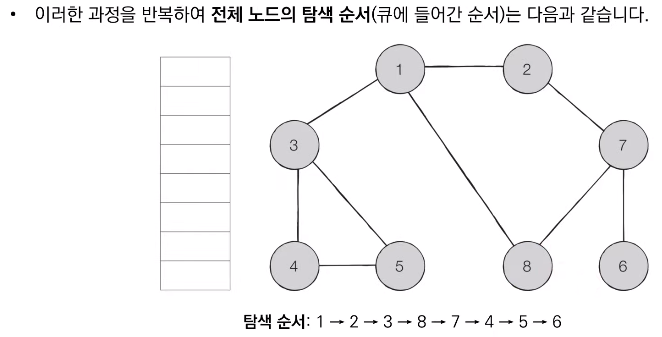
- 탐색 시작 노드를 큐에 삽입하고 방문 처리를 한다.
- 큐에서 노드를 꺼낸 뒤에 해당 노드의 인접 노드 중에서 방문하지 않은 노드를 모두 큐에 삽입하고 방문 처리한다.
- 더 이상 2번의 과정을 수행할 수 없을 때까지 반복한다.
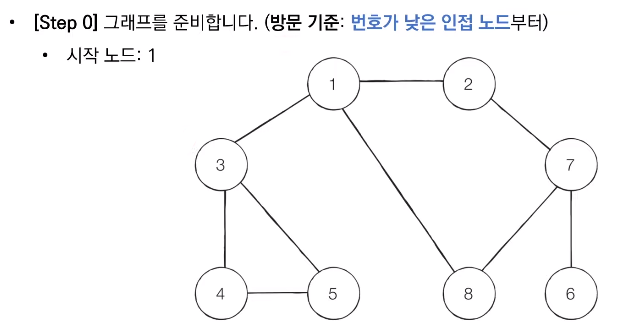
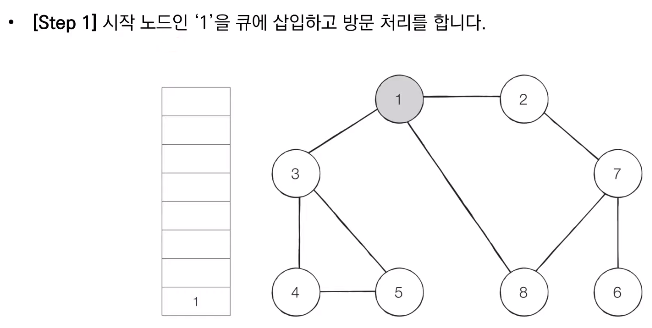
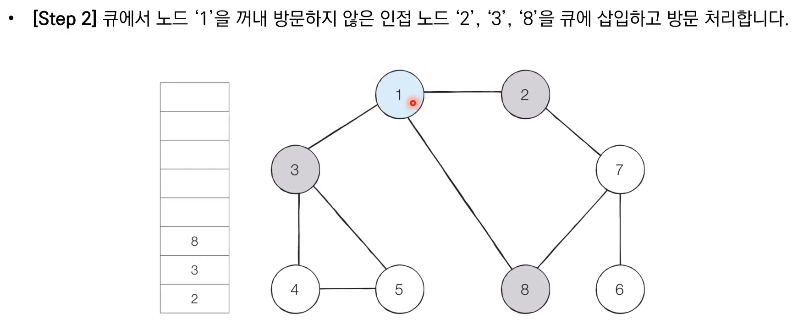
📝 코드 구현
import java.util.*;
public class Main {
public static boolean[] visited = new boolean[9];
public static ArrayList<ArrayList<Integer>> graph = new ArrayList<ArrayList<Integer>>();
// BFS 함수 정의
public static void bfs(int start) {
Queue<Integer> q = new LinkedList<>();
q.offer(start);
// 현재 노드를 방문 처리
visited[start] = true;
// 큐가 빌 때까지 반복
while(!q.isEmpty()) {
// 큐에서 하나의 원소를 뽑아 출력
int x = q.poll();
System.out.print(x + " ");
// 해당 원소와 연결된, 아직 방문하지 않은 원소들을 큐에 삽입
for(int i = 0; i < graph.get(x).size(); i++) {
int y = graph.get(x).get(i);
if(!visited[y]) {
q.offer(y);
visited[y] = true;
}
}
}
}
public static void main(String[] args) {
// 그래프 초기화
for (int i = 0; i < 9; i++) {
graph.add(new ArrayList<Integer>());
}
// 노드 1에 연결된 노드 정보 저장
graph.get(1).add(2);
graph.get(1).add(3);
graph.get(1).add(8);
// 노드 2에 연결된 노드 정보 저장
graph.get(2).add(1);
graph.get(2).add(7);
// 노드 3에 연결된 노드 정보 저장
graph.get(3).add(1);
graph.get(3).add(4);
graph.get(3).add(5);
// 노드 4에 연결된 노드 정보 저장
graph.get(4).add(3);
graph.get(4).add(5);
// 노드 5에 연결된 노드 정보 저장
graph.get(5).add(3);
graph.get(5).add(4);
// 노드 6에 연결된 노드 정보 저장
graph.get(6).add(7);
// 노드 7에 연결된 노드 정보 저장
graph.get(7).add(2);
graph.get(7).add(6);
graph.get(7).add(8);
// 노드 8에 연결된 노드 정보 저장
graph.get(8).add(1);
graph.get(8).add(7);
bfs(1);
}
}🔎<문제> 음료수 얼려 먹기
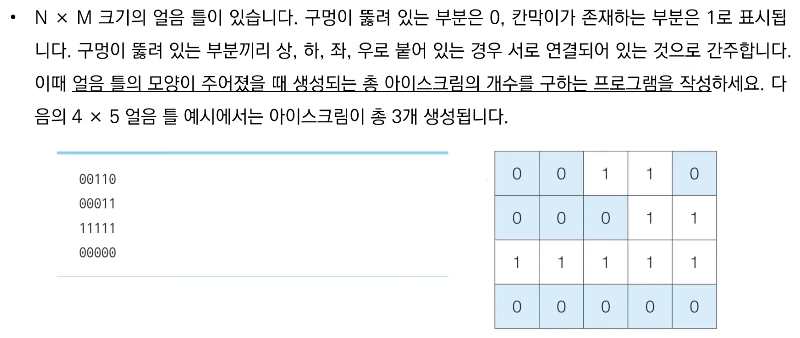

📝 문제 해결 아이디어
이 문제는 DFS 혹은 BFS로 해결할 수 있다. 일단 앞에서 배운 대로 얼음을 얼릴 수 있는 공간이 상, 하, 좌, 우로 연결되어 있다고 표현할 수 있으므로 그래프 형태로 모델링 할 수 있다.
다음과 같이 3 x 3 크기의 얼음 틀이 있다고 가정하고 생각해보자.
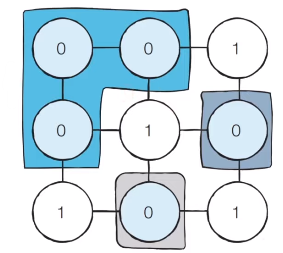
- DFS를 활용하는 알고리즘
- 특정한 지점의 주변 상, 하, 좌, 우를 살펴본 뒤에 주변 지점 중에서 값이 '0'이면서 아직 방문하지 않은 지점이 있다면 해당 지점을 방문한다.
- 방문한 지점에서 다시 상, 하, 좌, 우를 살펴보면서 방문을 진행하는 과정을 반복하면, 연결된 모든 지점을 방문할 수 있다.
- 모든 노드에 대해 1~2번의 과정을 반복하며, 방문하지 않은 지점의 수를 카운트 한다.
📝 답안 예시

import java.util.*;
public class Main {
public static int n, m;
public static int[][] graph = new int[1000][1000];
// DFS로 특정 노드를 방문하고 연결된 모든 노드들도 방문
public static boolean dfs(int x, int y) {
// 주어진 범위를 벗어나는 경우에는 즉시 종료
if (x <= -1 || x >=n || y <= -1 || y >= m) {
return false;
}
// 현재 노드를 아직 방문하지 않았다면
if (graph[x][y] == 0) {
// 해당 노드 방문 처리
graph[x][y] = 1;
// 상, 하, 좌, 우의 위치들도 모두 재귀적으로 호출
dfs(x - 1, y);
dfs(x, y - 1);
dfs(x + 1, y);
dfs(x, y + 1);
return true;
}
return false;
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
// N, M을 공백을 기준으로 구분하여 입력 받기
n = sc.nextInt();
m = sc.nextInt();
sc.nextLine(); // 버퍼 지우기
// 2차원 리스트의 맵 정보 입력 받기
for (int i = 0; i < n; i++) {
String str = sc.nextLine();
for (int j = 0; j < m; j++) {
graph[i][j] = str.charAt(j) - '0';
}
}
// 모든 노드(위치)에 대하여 음료수 채우기
int result = 0;
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
// 현재 위치에서 DFS 수행
if (dfs(i, j)) {
result += 1;
}
}
}
System.out.println(result); // 정답 출력
}
}🔎<문제> 미로 탈출


입력
5 6
101010
111111
000001
111111
111111📝 문제 해결 아이디어
- BFS는 시작 지점에서 가까운 노드부터 차례대로 그래프의 모든 노드를 탐색한다.
- 상, 하, 좌, 우로 연결된 모든 노드로의 거리가 1로 동일하다.
따라서 (1, 1) 지점부터 BFS를 수행하여 모든 노드의 최단 거리 값을 기록하면 해결할 수 있다. - 예시로 다음과 같이 3 x 3 크기의 미로가 있다고 가정하자.
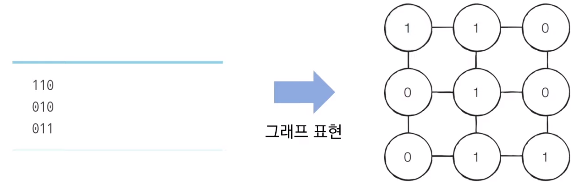
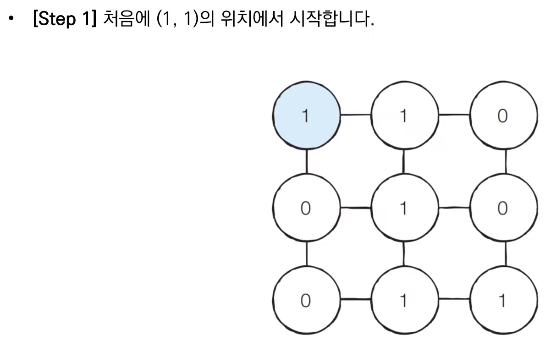
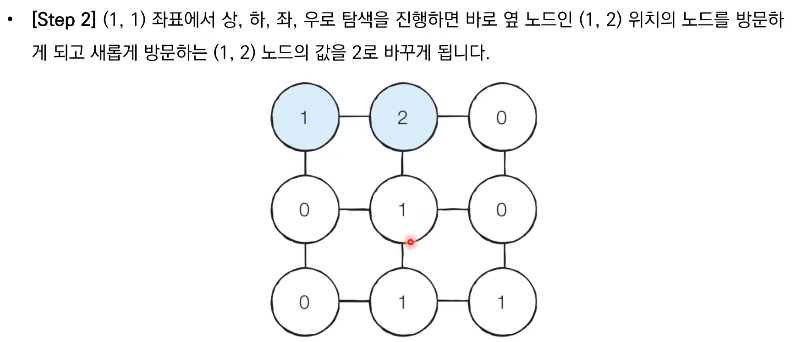
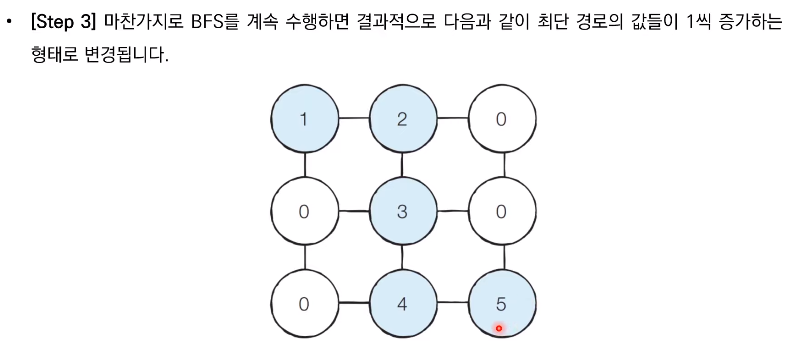
📝 답안 예시
import java.util.*;
class Node {
private int x;
private int y;
public Node(int x, int y) {
this.x = x;
this.y = y;
}
public int getX() {
return this.x;
}
public int getY() {
return this.y;
}
}
public class Main {
public static int n, m;
public static int[][] graph = new int[201][201];
// 이동할 네 가지 방향 정의 (상, 하, 좌, 우)
public static int dx[] = {-1, 1, 0, 0};
public static int dy[] = {0, 0, -1, 1};
public static int bfs(int x, int y) {
// 큐(Queue) 구현을 위해 queue 라이브러리 사용
Queue<Node> q = new LinkedList<>();
q.offer(new Node(x, y));
// 큐가 빌 때까지 반복하기
while(!q.isEmpty()) {
Node node = q.poll();
x = node.getX();
y = node.getY();
// 현재 위치에서 4가지 방향으로의 위치 확인
for (int i = 0; i < 4; i++) {
int nx = x + dx[i];
int ny = y + dy[i];
// 미로 찾기 공간을 벗어난 경우 무시
if (nx < 0 || nx >= n || ny < 0 || ny >= m) continue;
// 벽인 경우 무시
if (graph[nx][ny] == 0) continue;
// 해당 노드를 처음 방문하는 경우에만 최단 거리 기록
if (graph[nx][ny] == 1) {
graph[nx][ny] = graph[x][y] + 1;
q.offer(new Node(nx, ny));
}
}
}
// 가장 오른쪽 아래까지의 최단 거리 반환
return graph[n - 1][m - 1];
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
// N, M을 공백을 기준으로 구분하여 입력 받기
n = sc.nextInt();
m = sc.nextInt();
sc.nextLine(); // 버퍼 지우기
// 2차원 리스트의 맵 정보 입력 받기
for (int i = 0; i < n; i++) {
String str = sc.nextLine();
for (int j = 0; j < m; j++) {
graph[i][j] = str.charAt(j) - '0';
}
}
// BFS를 수행한 결과 출력
System.out.println(bfs(0, 0));
}
}DFS BFS 비교
📍소스 코드로 비교
DFS는 재귀적으로 호출되고, BFS는 큐에 다음 노드들을 넣는다.
따라서 DFS는 자신의 이웃 노드를 뒤로 미루고, BFS는 바로 탐색합니다. 그렇기 때문에 DFS는 깊이 우선으로 탐색하게 되고 BFS는 너비를 우선으로 탐색하게 된다.
📍문제 유형
DFS는 모든 경로 탐색에 유리한 특성을 가지고 있다.
BFS는 최단 경로(시작과 끝이 정해진) 탐색에 유리하다.
DFS : 모든 그래프 순회, 백트래킹, 트리 높이 계산, 이진탐색(후위, 전위 순회)
BFS : 최단거리, 최소 스탭(최소 동작), 동시 탐색(가능한 게임 상태 탐색), 이진탐색(중위 순회)

