Segment Tree
어떤 배열에서 특정 구간에 대한 합(최솟값, 최댓값, 곱 등)을 구할 때 사용되는 개념이다. 특정 구간에 대한 합을 구하는 가장 기본적인 방법으로는 구간 내의 값들을 for문으로 차례대로 하나씩 더하는 방법이 있다. 하지만 이 방법은 더해야 하는 값의 갯수가 N개라면 시간 복잡도는 0(N)이 되므로 속도가 너무 느리기 때문에 다른 효율적인 방법이 필요하다. 그래서 나온 개념이 이진 트리 구조로 만든 Segment Tree이고, 시간 복잡도는 0(logN)이므로 완전 탐색에 비해 속도가 훨씬 빠르다는 장점이 있다. 단점으로는 완전 탐색을 할 때보다 더 많은 메모리가 요구되므로 공간복잡도가 증가한다는 것이 있다.
Detail

lst = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
segment_tree = [0] * (N * 4)편의상 넉넉하게 Segment Tree의 크기를 lst의 갯수 N의 4배로 설정한다.
Segment Tree Init
Segment Tree를 초기화하는 부분을 재귀 함수를 이용하여 구현했다. Segment Tree의 root node의 index는 1~10 까지의 수 이므로 1~10의 node index를 가지고, 해당 node index의 위치에 arr의 특정 구간의 합 값이 삽입된다. 이는 start == end인 리프 node일 때까지 재귀적으로 구해지고, 부모 node는 두 자식 노드의 합 값으로 채워지는데, 즉, tree의 node index에 start부터 mid까지의 구간의 합과 mid부터 end까지의 합으로 채워진다는 것을 의미한다. 이 때, tree의 부모 node의 index를 i라고 할 때 자식 node의 index는 각각
i * 2,i * 2 + 1라고 한다. 결국 리프 node의 값이 들어가면서 재귀적으로 각 node의 값이 구해지게 되고, 최종적으로 루트 node의 값까지 채워지게 되어 Segment Tree의 초기화가 완료된다.
# Segment Tree 특정 구간의 합으로 채우기
# start는 구간의 시작 index, end는 구간의 끝 index, index는 tree node의 index로 1부터 시작
def init(start, end, index):
if start == end: # 자식 node가 없는 leaf node일 때
segment_tree[index] = lst[start - 1] # lst의 특정 index 값 삽입
return segment_tree[index]
# leaf node가 아닌 경우
# 두 구간으로 나누어 두 개의 자식 node에 각각 저장하기 위해 mid 값 계산
mid = (start + end) // 2
# segment_tree의 부모 node index의 값을 재귀적으로 두 자식 노드의 값의 합으로 채움
segment_tree[index] = init(start, mid, index * 2) + init(mid + 1, end, index * 2 + 1)
return segment_tree[index]구간 합 구하기
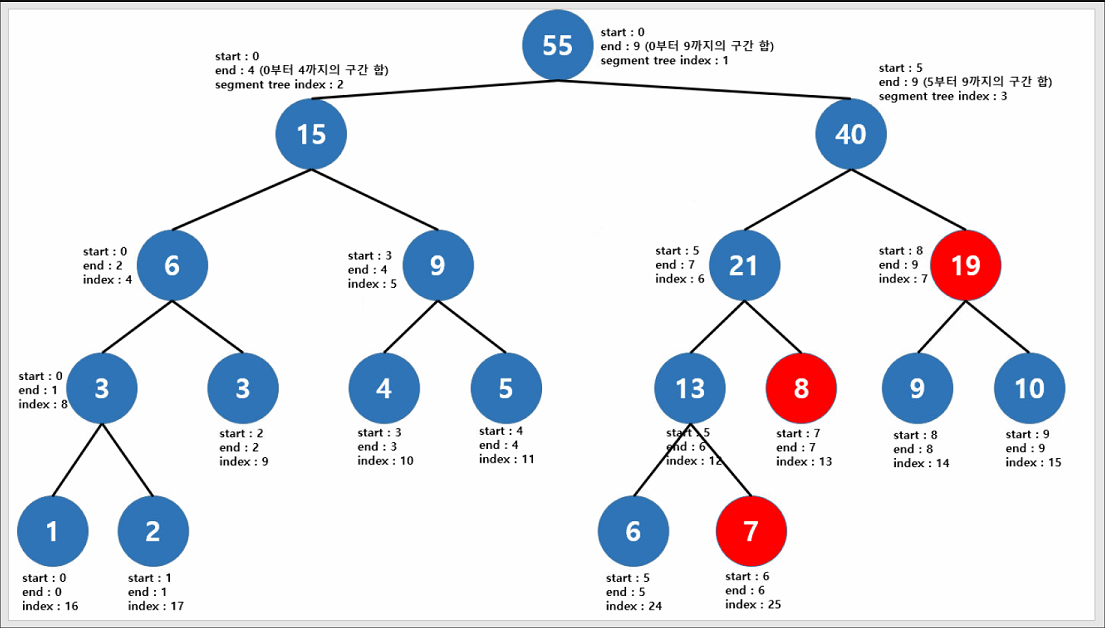
예를 들어 index 6~9 사이 구간의 값의 합을 구해야할 때 빨간색으로 칠해진 node의 합을 구하면 된다. 즉, 각 6~9 index에 해당하는 값들은 각각 7, 8, 9, 10이고, 빨간색 node를 더하면 7 + 8 + 19 = 34가 된다.
일반화하여 살펴보면 start index보다 right index 값이 작거나 end index보다 left index가 크다면 합을 구해야 할 구간에 속하지 않기 때문에 제외하고, start index가 left index보다 크거나 같고, end index가 right index보다 작거나 같은 경우에는 합을 구해야 할 구간에 속한 부분이다. 즉, 합을 구해야 할 구간에 속한 부분인 범위 내의 경우만 고려하여 합을 구해주면 된다.
# left, right는 특정 구간의 합을 구하고자 할 때의 범위 경계값의 index
def query(start, end, index, left, right):
# 범위 외의 경우일 때는 고려 x
if start > right or end < left:
return 0
# 범위 내의 경우일 때만 고려 o
if start >= left and end <= right:
return segment_tree[index]
# 위의 경우에 포함되지 않는 경우
# 구해야하는 left, right 범위가 start, end 사이에 존재하지만
# start, end 사이의 범위가 더 넓은 경우에
# 위의 조건에 맞도록 재귀적으로 반복되어 0 or 해당 node index
# 의 값이 더해질 수 있도록 아래와 같은 작업을 추가함
mid = (start + end) // 2
# 두 부분으로 나누어 위의 조건에 맞는 합을 재귀적으로 구해나감
sub_sum = query(start, mid, index * 2, left, right) + query(mid + 1, end, index * 2 + 1, left, right)
return sub_sumSegment Tree Update
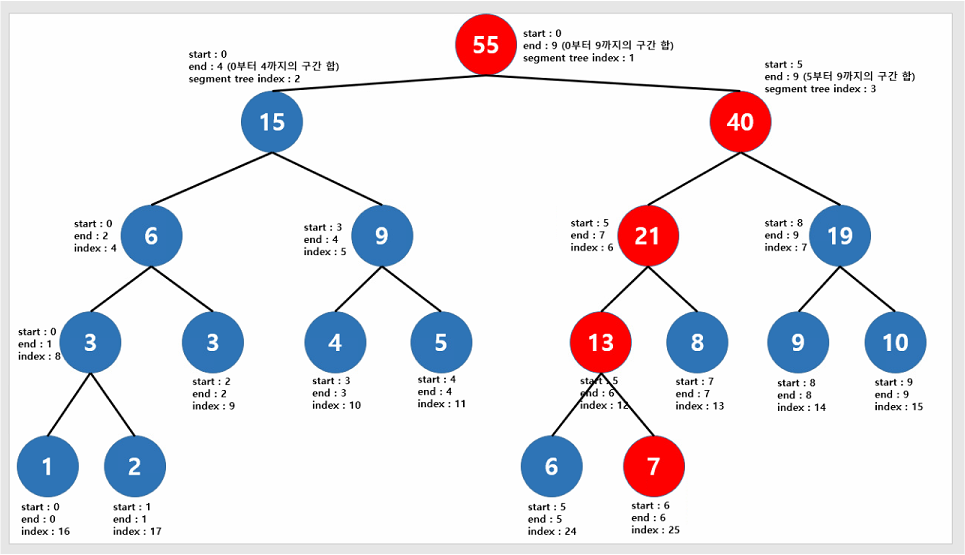
특정 leaf node의 값을 변경하게 되면 그 leaf node의 값을 포함하고 있는 Segment Tree 내의 부모 node들에 저장되어있는 구간 합 값도 변경되어야 한다. 즉, 변경된 leaf node를 포함하고 있는 부모 node들을 모두 update 해주면 된다. 이때 유의할 점은 Segment Tree의 모든 node를 변경하지 않고, 해당 leaf node의 값을 포함하고 있는 node들만 선별하여 update 해야한다.
예를 들면 index 6에 해당하는 leaf node의 값인 7을 변경할 때 해당 leaf node를 포함하는 부모 node(leaf node를 포함하는 구간의 합인 node), 즉, 위의 그림에서의 빨간색 node들의 값만 update를 해주면 된다. 이 함수도 재귀적으로 구현하고, 범위 내의 경우에 대해서만 update 한다.
# 특정 leaf node의 값이 변경될 때 Segment Tree를 update하는 함수
# update_idx : node에 저장되어 있는 구간 합 값을 수정하고자 하는 node의 index
# update_data : 기존 값과 변경된 값의 차이, 즉, 수정할 값
def update(start, end, index, update_idx, update_data):
# 범위 외의 경우일 떄는 고려 x
if start > update_idx or end < update_idx:
return
segment_tree[index] += update_data
# 범위 내의 경우일 때는 고려 o
if start == end:
return
# 범위 내의 경우에는 내려가면서 다른 node 값들 update
mid = (start + end) // 2
update(start, mid, index * 2, update_idx, update_data)
update(mid + 1, end, index * 2 + 1, update_idx, update_data)