[Data] 나이브 베이즈 분류와 모델링

🔎 나이브 베이즈 분류 (Naive Bayes classification)

• 데이터를 분류할 때 데이터 셋의 모든 특징들이 독립적이고 동등하다고 가정하고 데이터를 분류한다.
• 자료에 대한 가정을 하지 않고 대용량 데이터 자료에서 동작이 가능하다.
• 스팸필터 및 키워드 검색을 활용한 문서 분류에 사용된다.
• 베이즈 정리를 적용하여 데이터를 구성하고 각 변수는 독립적으로 가정해서 입력벡터를 분류하는 확률 모형이다
• 서포트 벡터 머신과 함께 우수한 분류 성능을 보이고 있다
• 범주형 예측자료만 가능 (수치형 자료의 경우, 범주형으로 변환해야 함)

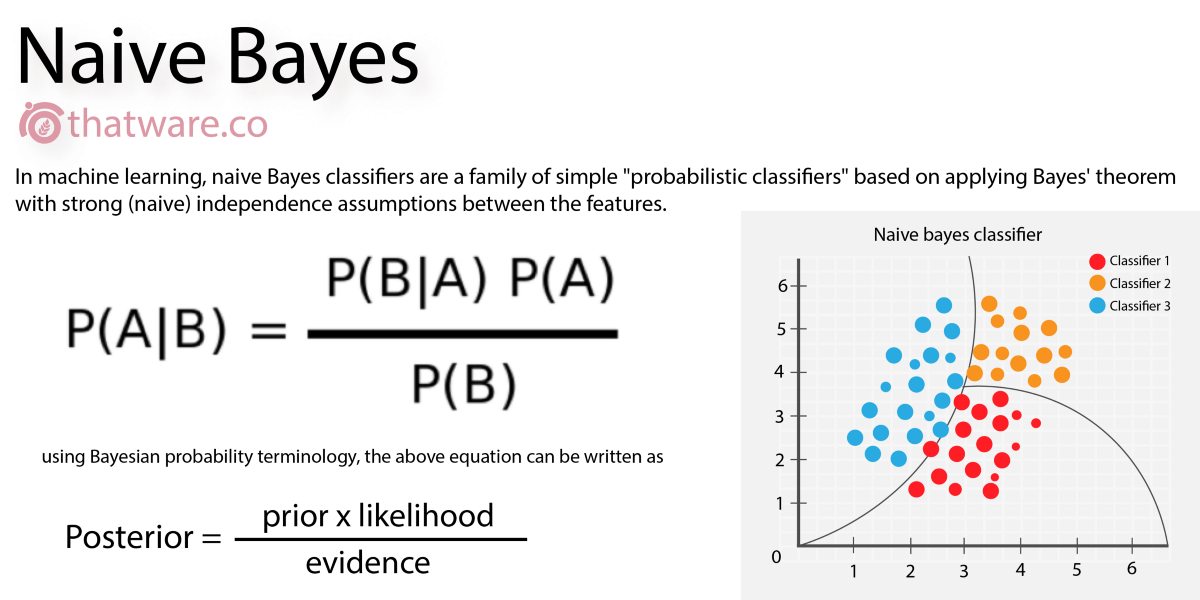
🔎 나이브 베이즈 알고리즘

P(A|B) = P(B|A)P(A)/P(B)

P(A|B) : 사건 B가 발생한 상태에서 사건 A가 발생할 조건부 확률
P(B|A) : 사건 A가 발생한 상태에서 사건 B가 발생할 조건부 확률
P(A) : 사건 A가 발생할 확률
P(B) : 사건 B가 발생할 확률

🔎 나이브 베이즈 장점

• 매우 단순하고 결측 데이터가 있어도 우수하다.
• 적은 학습 데이터로도 잘 수행된다.
• 메모리 사용량이 적다.
• 우수한 분류성능을 발휘한다.
• 계산과정의 복잡성이 낮기 때문에 성능이 빠르다.
• 예측에 대한 추정된 확률을 얻기가 쉽다

🔎 나이브 베이즈 단점

• 모든 속성을 독립적이고 동등하다는 가정에 의존한다.
• 변수들이 확률적이고 독립되지 않은 경우에 오류가 발생한다.
• 수치속성으로 구성된 데이터 셋에서는 우수하지 않다.
• 추정된 확률은 예측된 범주보다 신뢰가 떨어진다.
  
  

🔎 나이브 베이즈 모형 (scikit-learn)

사이킷런의 naive_bayes 서브패키지에서 제공하는 나이브베이즈 모형 클래스

< 사전 확률과 관련된 속성 >

- classes_ : 종속변수 Y의 클래스(라벨)

- class_count_ : 종속변수 Y의 값이 특정한 클래스인 표본 데이터의 수

- class_prior_ : 종속변수 Y의 무조건부 확률분포 P(Y) (정규분포의 경우에만)

- class_log_prior_ : 종속변수 Y의 무조건부 확률분포의 로그 logP(Y) 
  (베르누이분포나 다항분포의 경우에만)

1. GaussianNB: 정규분포 나이브베이즈

가우시안 나이브베이즈 모형 GaussianNB은 가능도 추정과 관련하여
다음과 같은 속성을 가진다.

- theta_: 정규분포의 기댓값 μ
- sigma_: 정규분포의 분산 σ2

2. BernoulliNB: 베르누이분포 나이브베이즈

3. MultinomialNB: 다항분포 나이브베이즈

자세한 내용은 해당 글 참고