[자료구조] 힙자료구조 - heapq모듈 활용

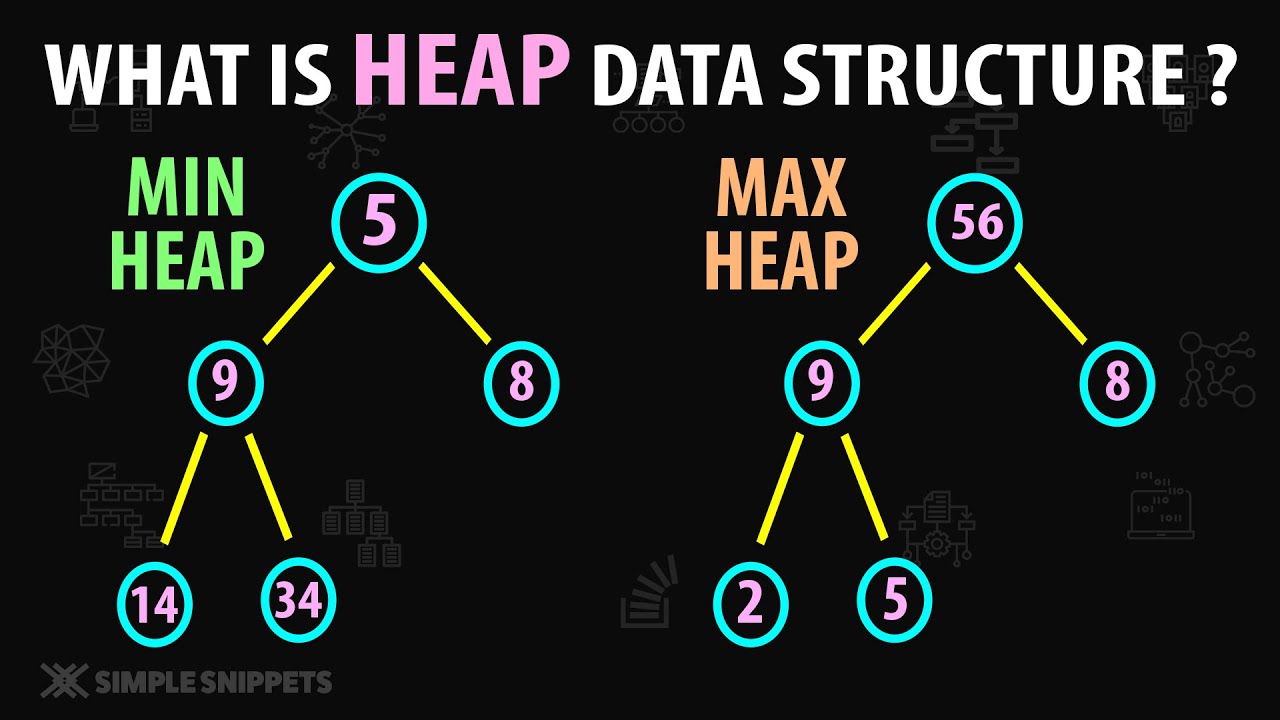
heap이란?

우선순위의 개념을 큐에 도입한 자료구조로 우선순위가 높은 데이터가 먼저 나가게 된다. 이진 트리(binary tree) 기반으로 최소 힙(min heap) 자료구조를 제공한다.

heap의 종류

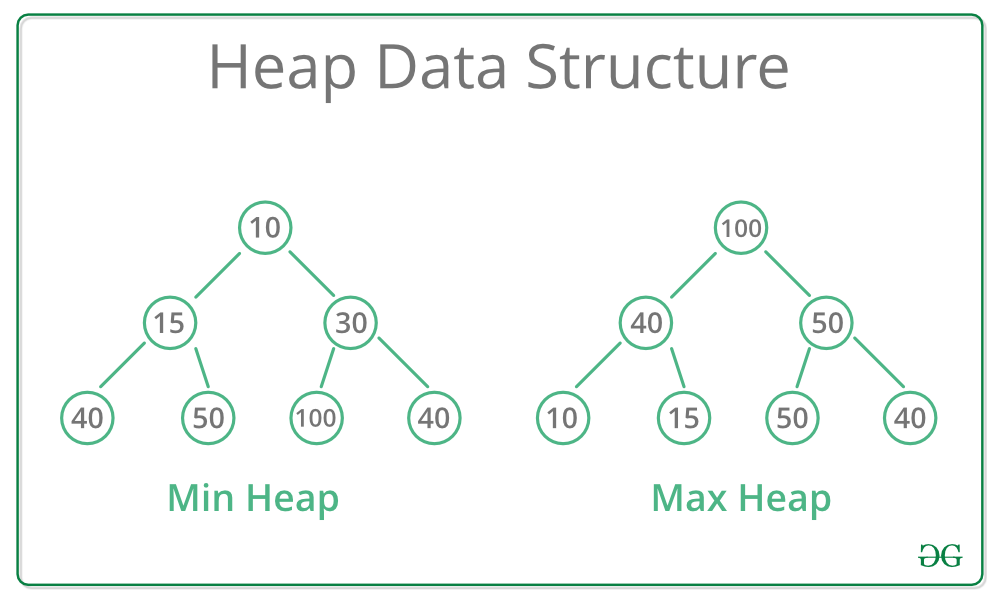
• 최대 힙(max heap)
  부모 노드의 키 값이 자식 노드의 키 값보다 크거나 같은 완전 이진 트리

• 최소 힙(min heap)
  부모 노드의 키 값이 자식 노드의 키 값보다 작거나 같은 완전 이진 트리

heapq 모듈 활용 소스코드

heapq 모듈 import

from heapq import heappush, heappop

최소 힙 생성

heap = []

힙에 원소 추가

from heapq import heappush
heappush(heap, 4)
heappush(heap, 1)
heappush(heap, 7)
heappush(heap, 3)
print(heap)

힙에서 원소 삭제

from heapq import heappop
print(heappop(heap))
print(heap)

최소값 삭제하지 않고 얻기

print(heap[0])

기존 리스트를 힙으로 변환

from heapq import heapify
heap = [4, 1, 7, 3, 8, 5]
heapify(heap)
print(heap)

nums = [4, 1, 7, 3, 8, 5]
heap = nums[:]
heapify(heap)
print(nums)
print(heap)

최대 힙

• 힙에 튜플(tuple)를 원소로 추가하거나 삭제하면, 튜플 내에서 맨 앞에 있는 값을 기준으로 최소 힙이 구성되는 원리를 이용
• 각 값에 대한 우선 순위를 구한 후, (우선 순위, 값) 구조의 튜플을 힙에 추가하거나 삭제!
• 힙에서 값을 읽어올 때는 각 튜플에서 인덱스 1에 있는 값을 취하자
  (우선 순위에는 관심이 없으므로 )

from heapq import heappush, heappop
nums = [4, 1, 7, 3, 8, 5]
heap = []
for num in nums:
  heappush(heap, (-num, num))  # (우선 순위, 값)
while heap:
  print(heappop(heap)[1])  # index 1

n번째 최소값/최대값

• 최소 힙이나 최대 힙을 사용하면 n 번째로 작은 값이나 n 번째로 큰 값을 효과적으로 구할 수 있다
• n 번째 최소값을 구하기 위해서는 주어진 배열로 힙을 만든 후, heappop() 함수를 n 번 호출

from heapq import heappush, heappop
def nth_smallest(nums, n):
    heap = []
    for num in nums:
        heappush(heap, num)
    nth_min = None
    for _ in range(n):
        nth_min = heappop(heap)
    return nth_min
print(nth_smallest([4, 1, 7, 3, 8, 5], 3))

# heapify 사용해서 반복문 줄이기
def nth_smallest(nums, n):
    heapify(nums)
    nth_min = None
    for _ in range(n):
        nth_min = heappop(nums)
    return nth_min
print(nth_smallest([4, 1, 7, 3, 8, 5], 3))

• nsmallest(), nlargest() : 주어진 리스트에서 가장 작은/큰 n개의 값을 담은 리스트를 반환 (리스트의 마지막 값이 n 번째 작은/큰 값)

from heapq import nsmallest
nsmallest(3, [4, 1, 7, 3, 8, 5])[-1]

from heapq import nlargest
nlargest(3, [4, 1, 7, 3, 8, 5])[-1]

힙 정렬

from heapq import heappush, heappop
def heap_sort(nums):
  heap = []
  for num in nums:
    heappush(heap, num)
  sorted_nums = []
  while heap:
    sorted_nums.append(heappop(heap))
  return sorted_nums
print(heap_sort([4, 1, 7, 3, 8, 5]))