[통계학] - 통계 분석방법 총정리 & 사용순서

🔎 통계학의 이해도를 높여주는 도표

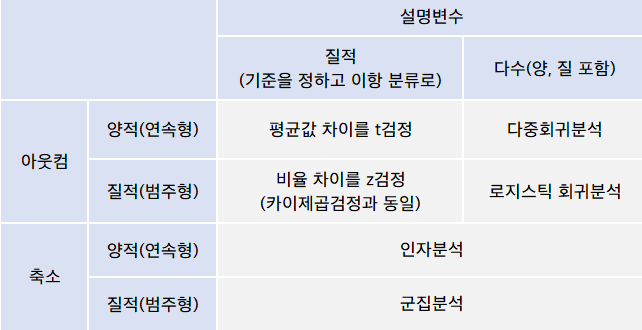
• 설명변수가 질적이라면, 기준 카테고리를 정해놓고 이항으로 분류
  • 수백 건 이상의 데이터가 있으므로 실용측면에서는 z검정
  • 더 확실히 검정한다는 의미로 평균값의 차이에 관해선 t검정
  • 비율 차이는 데이터 수가 적더라도 문제 없으므로 z검정이나 카이제곱검정
• t검정 / z검정, 카이제곱검정과 동일한 결과
  • t검정 : '두 값의 설명변수를 하나만 사용한 다중회귀분석(단순회귀분석)
  • z검정, 카이제곱검정 : '두 값의 설명변수를 하나만 사용한 로지스틱 회귀분석

🔎 비즈니스에서 활용하는 경우 분석 순서

1. 다중회귀분석 / 로지스틱 회귀분석으로 관련성 분석

1) 대략적인 데이터 정리와 확인
2) 최대화 혹은 최소화해야 할 아웃컴이 무엇인지 정함
3) 그 이외의 모든 항목을 설명변수의 후보로 놓고 다중회귀분석 or 로지스틱 회귀분석 (설명변수가 지나치게 많은 상황 방지를 위해 변수 선택법 사용)

2. 결과 해석

1) '이익을 올려주는 아이디어'를 한번에 발견! > GOOD
2) '여러 설명변수와 아웃컴의 관련성이 나타나지만 석연치 않음' > 설명변수의 선별 선택

💡 [ 설명변수의 선별 선택 ]

• 아웃컴과의 관련성이 너무 당연한 듯 보이는 설명변수는 p-값이 아무리 작아도 제외 (ex. 구매상품이 증가할 때마다 구매금액이 증가)

• 당연한 설명변수가 포함되어 있을 땐, 다른 설명변수에 관한 회귀계수를 해당 설명변수의 회귀계수와 비교하는 것을 유의

• 특정한 회귀계수의 해석을 어렵게 만드는 설명변수는 제외
  (ex. '다른 설명변수의 값이 동일하다는 가정하에서')

• 설명변수의 취급방법을 바꾸는 것이 나을 때도 존재
  (ex. 양적변수 : 나이 > 질적변수 : 세대)

• 꼭 포함되어야 하는 설명변수가 자동 변수선택 과정에서 삭제되었을 경우에는, 강제로라도 그 설명변수를 포함

설명변수 선별선택과 결과 해석 과정에서 '인자분석'과 '군집분석' 사용하면 결과에 도움이 됨

💡 [ 분석결과에서 아이디어를 찾아내는 방법 ]

이익창출을 위한 아이디어

1) 아웃컴과 관련된 설명변수가 광고나 상품생산, 연수 등에 의해 '조정'이 가능하다면 그 설명변수를 조정하는 것이 이익을 낳는 아이디어

2) 현시점에서 '신뢰할 수 있다'고 생각할 만한 목표로 설정한 시장의 고객은 몇사람이나 되는지 파악하고 설명변수를 조정

• '조정'할 수 없는 설명변수와 아웃컴 사이의 관련성은 '재배치' 진행

3) '조정'도 '재배치'도 불가능한 설명변수는 다른 관점 활용

• ex. 계절과 날씨에 따른 제품 판매량 변화 : 계절이나 날씨에 맞춰 사전에 필요한 물품의 구입이나 생산, 재고 상태를 예측하여 최적화
  
  

3. 임의화 비교실험이나 A/B 테스트로 검정

'신뢰할 수 있으므로 상품을 많이 샀다'인지 
'상품을 많이 샀기 때문에 신뢰가 생겨난 것'인지는
 회귀계수나 p값을 봐도 알 수 없음!

💥'상관'과 '인과'를 혼동해서는 안됨

• 이익이 될 것 같은 아이디어를 찾았으면, 적절한 임의화 비교실험 또는 A/B 테스트를 통해 검정하자!

[ A/B 테스트 ]

1) 일정한 인원수 이상을 모아 반반씩 나눔

• 일정한 인원수 이상을 구하는 법
  • 평균값의 차이든 비율 차이든 검정력에 따라 '표준오차의 몇 배 차이가 예상되는가'라는 관점에서 추측

2) 나눈 그룹에 다른 방법 시행

• A그룹 (실험군) : 새로운 방법을 시험하는 그룹,
• B그룹 (대조군) : 기존의 방법을 실행하는 그룹
  ※ '충분히 많은 수의 대상'

3) A그룹과 B그룹 아웃컴 비교

• A그룹의 아웃컴이 B그룹에 비해 우연한 오차라고 생각할 수 없을 정도로 높다면, 통계적 가설검정에 의해 인과관계가 나타나는 것으로 생각해도 무방
  ▶️ 이때, t검정이나 z검정 사용

🔎 한걸음 나아간 통계학 공부

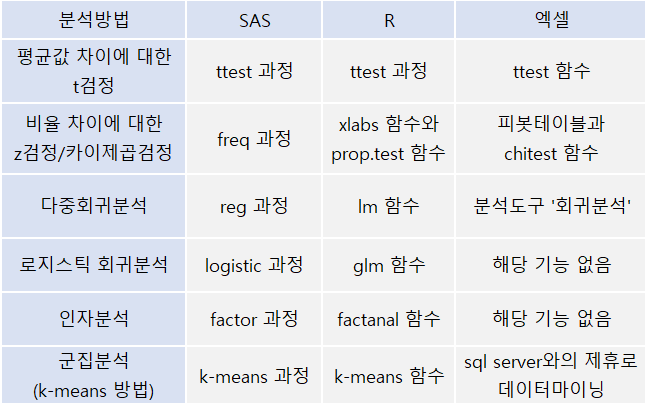
1. 새로운 아이디어 탐색 분석

• 회귀모형에 의한 아이디어 탐색 단계에서 '시간적인 요소'를 분석할 수 있게 됨
  
  

1) 생존분석

• '언제 탈퇴했는가' 와 같은 생존시간을 분석

• 콕스회귀분석

  - 분석환자의 생존시간을 분석하기 위해 생긴 방법
  - 오즈비가 아닌 하자드비(hazard ratio)라는 지표를 활용
  - '일정 시간당 몇 배의 확률로 일어나기 쉬운가/어려운가'라는 결과

  
  

2) 시계열 분석

• 같은 사람이나 물건을 대상으로 여러 차례 얻어낸 데이터를 '시계열 데이터'

• '과거의 정보와 다음 주 매출의 관계성은 어떠한가'를 생각하는 것

• 자기상관

  • '같은 매장의 데이터는 시점이 달라도 상관하여 일치한다'
  • '시간적 변동'을 포착
    ex. 바로 직전의 값뿐만 아니라 몇 시점 전 값의 크기와 관련성이라든가 시점을 불문하고 공통되는 평균값과 분산을 가진 변동 요인이 배후에 있는가
    

3) 경시데이터 분석

• 다른 설명변수와의 관계성을 분석하는 방법

• '사람마다 제각각'이라는 요인을 일반적인 회귀계수로 표현
  ▶ 1명을 기준으로 '인원수-1'개분의 더미변수 필요

• 혼합효과모형 사용
  
  

2. 새로운 축소

• 잠재적 인자 간의 관계성이 중요

• 구조방정식 모형

  • 축소를 할 뿐만 아니라, 직간접적으로 변수 사이의 다양한 관계성을 명백히 하는 분석방법

• 항목반응이론

  • 사실을 바탕으로 그 배후에 있는 잠재적 능력을 추정하고 사안별로 '잠재적인 능력'을 어떻게 식별할지를 명백히 규정하는 것

• 커널 k-means 방법

  • 커널함수를 이용하여 k-means 방법으로는 판별이 불가능한 형상의 군집으로 분류 가능한 방법

3. 임의화 비교실험 검정

• 통계적 인과추론

  • '임의화 비교실험이 불가능한 상황에서 어떻게 착오없이 검정하는가'

  • DM 발송여부에 따른 매출 차이 확인

    • 편중 존재
    • '발송의 결과로 매출이 오른것인지', '매출에 영향이 미칠 만한 사람에게 발송했기 때문에 매출이 오른 것인지' 구별 어려움