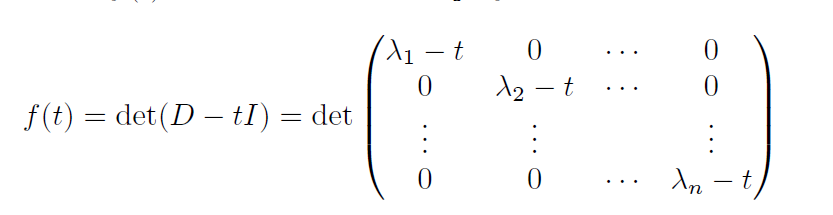1. Intro
이전의 장에서 어떤 선형연산자가 대각화가능하기 위한 필요충분 조건은 해당 연산자의 고유벡터로 이루어진 순서기저가 존재해야 한다고 했다. 하지만 모든 선형연산자 혹은 행렬이 항상 대각화할 수 있는 것은 아니다. 이번에는 구체적으로 대각화가능을 판별하고, 고유벡터로 이루어진 순서기저를 찾는 방법을 다뤄보도록 하자.
2. 고유벡터, 고유공간
고유값은 특성다항식 f(t)=det(A−tIn)의 근을 찾는 과정에서 발견할 수 있으며, 고유벡터는 고유값 λ를 이용해 Ax=λx를 통해 찾을 수 있다. (항상 이 방법으로 찾을 수 있는 것은 아니다.) 이렇게 찾은 고유벡터들을 모두 일차독립이다.
정리 1. 벡터공간의 선형연산자 T와 T의 서로 다른 고유값 λ1,…λk를 생각해보자.각 i=1,…k에 대하여 λi에 대응하는 고유벡터로 이루어진 유한집합 Sk를 생각해보자. 각 Si가 일차독립이면, S1∪…Sk도 일차독립이다.
증명
수학적 귀납법을 통해 증명해보자.
(1) k=1인 경우 증명할 필요가 없다.
(2) k≥2인 경우를 생각해보자.
이때 k−1개의 서로 다른 고유값에 대해 위의 정리가 성립한다고 가정하자. 이때 전체 고유값은 k개이므로 부분집합 Si={vi1,vi2,…,vini}가 λi에 대응하는 일차독립인 고유벡터의 집합이라 해보자. 이때, 전체 집합 S=S1∪⋯∪Sk가 일차독립임을 증명하면 된다.
다음 식을 만족하는 임의의 스칼라 aij를 생각해보자.
i=1∑kj=1∑niaijvij=0
즉, 각 λi에 대응하는 고유벡터의 선형결합을 나타낸 것이다.
이때 이에 대해 두가지 연산을 가할 것이다. 모두 특성다항식을 적용한 결과이다.
Ai=1∑kj=1∑niaijviji=1∑kj=1∑niaijAviji=1∑kj=1∑niaijλivij=0=0=0
첫번째 연산 결과는 위와 같다. 단순히 행렬 A를 가한 것이다.
λki=1∑kj=1∑niaijviji=1∑kj=1∑niaijλkvij=0=0
두번째 연산 결과는 위와 같다. 이번엔 λk를 가했다.
위 두 연산의 결과를 빼면 다음과 같은 수식이 도출된다.
i=1∑k−1j=1∑niaij(λi−λk)vij=0
그런데 이미 S1∪⋯∪Sk−1이 선형독립이라 가정했기 때문에, i=1…k−1에 대해서 aij(λi−λk)=0이다. 이때, 각 고유값은 서로 다른 값이므로 λi−λk=0이므로, i=1…k−1에 대하여 aij=0이 된다. 이는 자연스럽게 ∑j=1nkakjvkj=0임을 알 수 있다. 이때, Sk도 선형독립이기 때문에, j=1…nk에 대하여 akj=0이다.
그러므로 i=1…k와 j=1…ni에 대하여 aij=0이고, S는 선형독립이다.
선형연산자 T의 고유벡터가 서로 선형독립임을 이용하면, 한가지 따름정리가 추가적으로 나오게 된다.
따름정리. n차원 벡터공간의 선형연산자 T가 서로다른 n개의 고유값을 가지면 T는 대각화가능하다.
증명
T에 서로다른 n개의 고유값, λ1…λn이 있다고 가정할 때, 각 고유값에 대응하는 임의의 고유벡터 v1,…vn을 선택하자. 이때 위의 정리 1에 의하여 {v1,…,vn}은 선형독립이고, dim(V)=n이다. 결국 고유벡터로 만든 집합은 V의 기저가 된다. 이는 결국 T가 대각화가능하다는 것을 의미하게 된다.
지금까지 고유벡터와 대각가능화에 대해 살펴봤는데 좀 더 넓혀서 특성다항식과 대각가능성에 대해 살펴보도록 하자.
정의 1. 다음 조건을 만족하는 다항식 f(t) \in P(F)를∗∗F$ 위에서 완전히 인수분해된다**고 한다. 이때 스칼라 c,a1,…,an∈F 중 같은 값이 있을 수 있다.
같은 값이 있다는 것은 중근을 의미하게 되고, 더 중요한 점은 체 F 위에서 완전히 인수분해 되어야 한다는 점이다. 실수 공간에서 인수분해 되지 않는 특성다항식도 복소수 공간으로 옮기면 인수분해 될 수 있기 때문이다.
위의 정의를 이용해 특성다항식과 대각화가능성을 연결할 수 있다.
정리 2. F-벡터공간 V의 대각화가능한 선형연산자의 특성다항식으 F 위에서 완전히 인수분해된다.
증명
n차원 벡터공간 V의 대각가능한 선형연산자 T에 대하여 [T]β=D가 대각행렬이 되도록 하는 순서기저를 β라 하면 D는 다음과 같은 모양이 될 것이다.

이때 특성다항식 f(t)는 다음의 꼴이 된다. 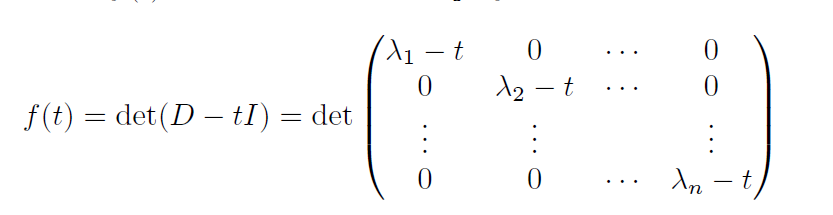
f(t)=(λ1−t)(λ2−t)(λ3−t)…(lambdan−t)=(−1)n(t−λ1)(t−λ2)…(t−λn)
결국 자연스레 특성다항식은 F위에서 완전히 인수분해되는 것을 볼 수 있다. 이때 각 고유값들은 서로 다를 필요가 없는 것을 알 수 있다.
이렇게 고유값을 찾는 과정에서 중근이 발생하는 것과 연관된 개념이 하나 있다.
정의 2. 특성다항식이 f(t)인 선형연산자의 고유값 λ에 대하여, (t−λ)k이 f(t)의 인수가 되도록 하는 가장 큰 자연수 k를 λ의 중복도라 한다.
즉, λ=4가 3번 중복되는 중근이라면, λ=4의 중복도는 3이 된다.
지금까지 고유값 λ에 대응되는 고유벡터는 T−λI의 영공간에 속하는 영이 아닌 벡터임을 증명하는 과정이었다. 그렇다면 T−λI의 영공간은 어떻게 되어 있을까?
정의 3. 벡터공간 V의 선형연산자 T와 고유값 λ에 대하여, 다음집합 Eλ를 λ에 대응하는 T의 고유공간이라 한다.
Eλ={x∈V:T(x)=λx}=N(T−λIv}
위 정의는 행렬에 대해서도 동일하게 적용된다. 그런데 Eλ는 당연하게도 고유벡터와 영벡터로 이루어져있게 된다. 즉, Eλ의 차원은 선형독립인 고유벡터의 최대 개수가 된다. 이는 결국 λ의 중복도와 Eλ의 차원이 연관되어 있음을 의미하게 된다.
정리 3. 유한차원 벡터공간 V의 선형연산자 T와 중복도가 m인 고유값 λ에 대하여 a≤dim(Eλ)≤m이다.
증명
Eλ의 순서기저를 확장하여 V의 순서기저 β를 만들자. 그리고 A=[T]β에 대하여 λ에 대응하는 고유벡터를 vi라고 표기하도록 하자. 이때, A 는 다음과 같은 꼴로 표현할 수 있다.
A=(λIpOBC)
이때 A의 특성다항식은 다음과 같이 표현될 수 있다.
f(t)=det(A−tIn)=det((λ−t)IpOBC−tIn−p)=det((λ−t)Ip)⋅det(C−tIn−p)=(λ−p)pg(t)
즉, A의 특성다항식 f(t)는 (λ−t)p을 인수로 가지게 된다. 이때 λ의 중복도는 최소 p가 된다. dim(Eλ)=p이기 때문에, dim(Eλ)≤m이 된다.
결국 각 고유값의 중복도는 각 고유공간의 차원과 동일하다. 그리고 고유공간의 기저는 각 교유값에 대응하는 고유벡터를 통해 생성된다. 또한, 모든 고유공간의 기저의 합집합은 본래 선형변환의 기저를 이루게 되는 것이다. 이것이 대각화가 의미하는 바가 된다.
2. 대각화가능 판정
지금까지 다룬 내용을 정리하면 다음과 같다.
정리 4. 유한차원 벡터공간 V의 선형연산자 T에 대하여 T의 특성다항식이 완전히 인수분해되고 , λ1,…,λk가 서로 다른 고유값일 때, 다음이 성립하게 된다.
- T가 대각화가능하기 위한 필요충분조건은 모든 i에 대하여 λi의 중복도가 dim(Eλi)와 같은 것이다.
- T가 대각화가능하고 각각의 i에 대하여 βi가 Eλi의 순서기저일때, β=β1∪β2⋯∪βk는 T의 고유벡터로 이루어진 순서기저이다.
증명
각 i에 대하여 mi는 λi의 중복도, di=dim(Eλi), n=dim(V)라고 하자.
우선 T가 대각화가능하다고 가정하고, T의 고유벡터로 이루어진 V의 기저를 β로 표기한다. 각 i에 대해 βi=β∩Eλi로 각 고유값에 대응하는 고유벡터로 이루어진 집합이 될 것이다. 이때 βi의 벡터의 개수를 ni로 표기해본다면, ni≤di일 수 밖에 없다. β1는 차원이 di인 부분공간에서 일차독립인 부분집합이기 때문이다. 그리고 앞서 정리했듯이 di≤mi이다.
β는 결국 n개의 벡터로 구성되어 있으므로 ni의 합은 n이 될 수밖에 없다. 이때, T의 특성다항식의 차수 역시 각 고유값의 중복도의 합과 같기 때문에 mi의 합 역시 n이 된다. 즉, 정리하자면 다음과 같다
n=i=1∑kni≤i=1∑kdi≤i=1∑kmi=n
위 식을 조금 정리하면 모든 i에 대하여 (mi−di)≥0이므로, mi=di이다. 그러므로 ∑i=1k(mi−di)=0이다.
여기서 조금더 나아가서, 역으로 증명해보도록하자. 즉, mi=di일 때 대각화가능하고 각 고유공간의 기저의 합은 본 공간의 순서기저임을 보일 것이다.
각 i에 대하여 Eλi의 순서기저를 βi라 하자. β=β1∪β2∪⋯∪βk라 하면, 이전의 정리에 의해 β는 선형독립이다. 이때, di=mi임을 가정했으므로, β는 ∑i=1kdi=∑i=1kmi=n개의 벡터로 구성되어 있다. 결국 β는 V의 고유벡터로 이루어진 순서기저이고, T는 대각화가능하게 된다.
대각화가능 여부 판정법은 결국 두가지 조건으로 구성되게 된다.
- T의 특성다항식이 완전히 인수분해된다.
- T의 고육밧의 중복도가 nullity(T−λI)와 같다.
또한 이를 대각화 자체와 이어서 생각해보면 대각화 가능한 n×n행렬 A에 대하여 다음 식을 만족하는 행렬 Q,D는 항상 존재하게 된다.
D=Q−1AQ
이때, D의 대각성분은 A의 고유값이 되고, Q의 열벡터는 각 고유값에 대응하는 고유벡터가 된다. 또한, Q가 n×n의 가역행렬이다.