Linear models
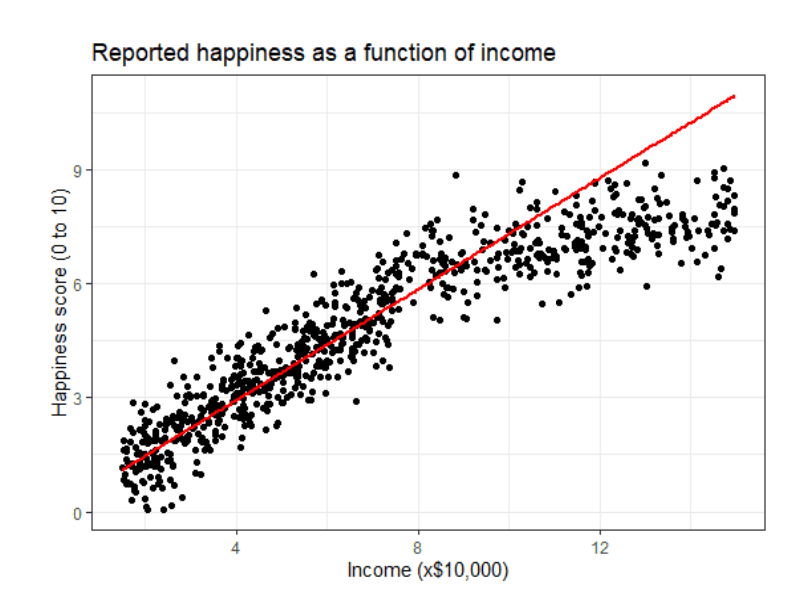
Hypothesis set : 직선 집합
hθ(x)=θ0+θ1x1+⋯+θdxd=θTx
확장된 선형 모델 :
hθ(x)=θ0+θ1k1(x1)+⋯+θdkd(xd)=θTk(x)
입력 x에 임의의 함수 ki(xi)를 적용해도 여전히 θ에 대해서 선형(linear)
장점
-
단순(simplicity)
해석이 가능함
-
일반화(Generalization)
Etest≈Etrain 가 쉬움
과적함이 잘 안됨
-
regression, classification 에 모두 사용 가능
Feature organization
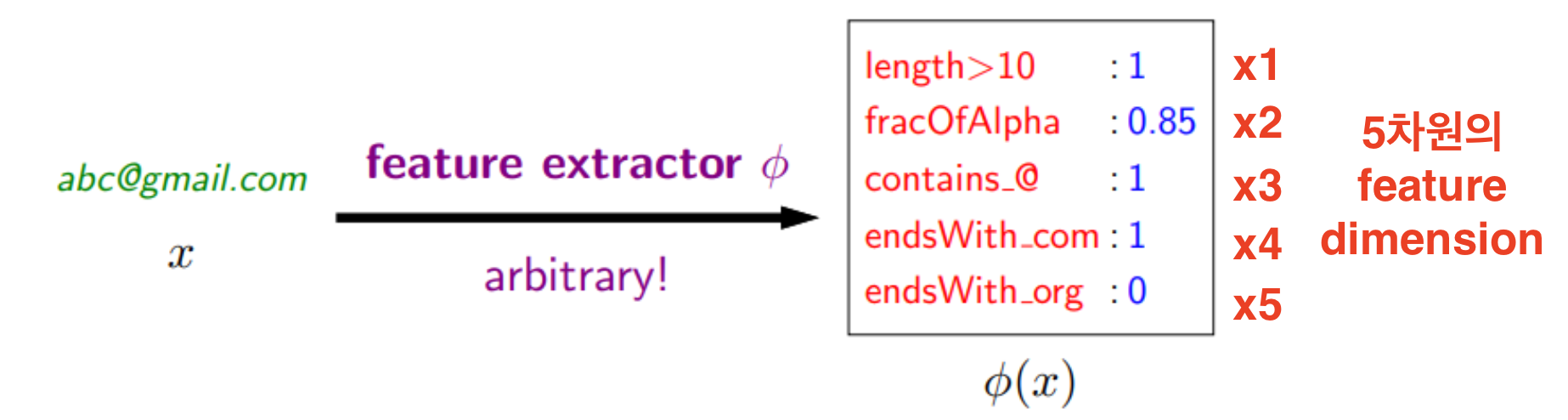
hθ(x)=θ0+θ1k1(ϕ(x)1)+⋯+θdkd(ϕ(x)d)=θTk(ϕ(x))
Linear regression framework
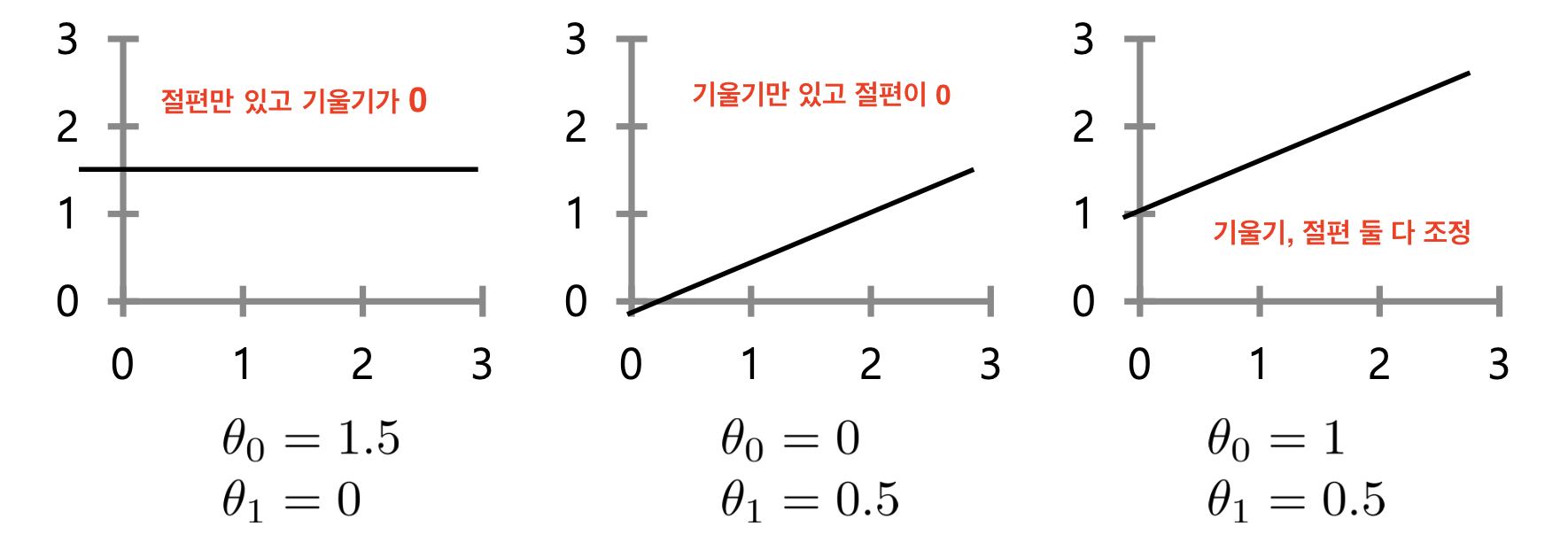
1차원 선형 회귀 구성 방식
가설 함수(모델) 선택 (Hypothesis class)
hθ(x)=θ0+θ1x
Loss function
MSE (Mean Squared Error)
J(θ)=2m1i=1∑m(hθ(x(i))−y(i))2
Optimization
경사하강법(Gradient Descent)
θj←θj−α∂θj∂J(θ)
학습률 α를 정해두고,
MSE를 줄이는 방향으로 매개변수 θ0,θ1 를 조금씩 업데이트
Linear regression: parameter opt.
hθ(x)=θ0+θ1x의 계수 θ0,θ1를 고르는 방식
L2 cost function (Goal : minimizing MSE)
Cost function J(θ0,θ1)
J(θ0,θ1)=2m1i=1∑m(hθ(x(i))−y(i))2
: 현재의 직선(파라미터)으로부터 데이터가 평균적으로 얼마나 떨어져 있는지 표현
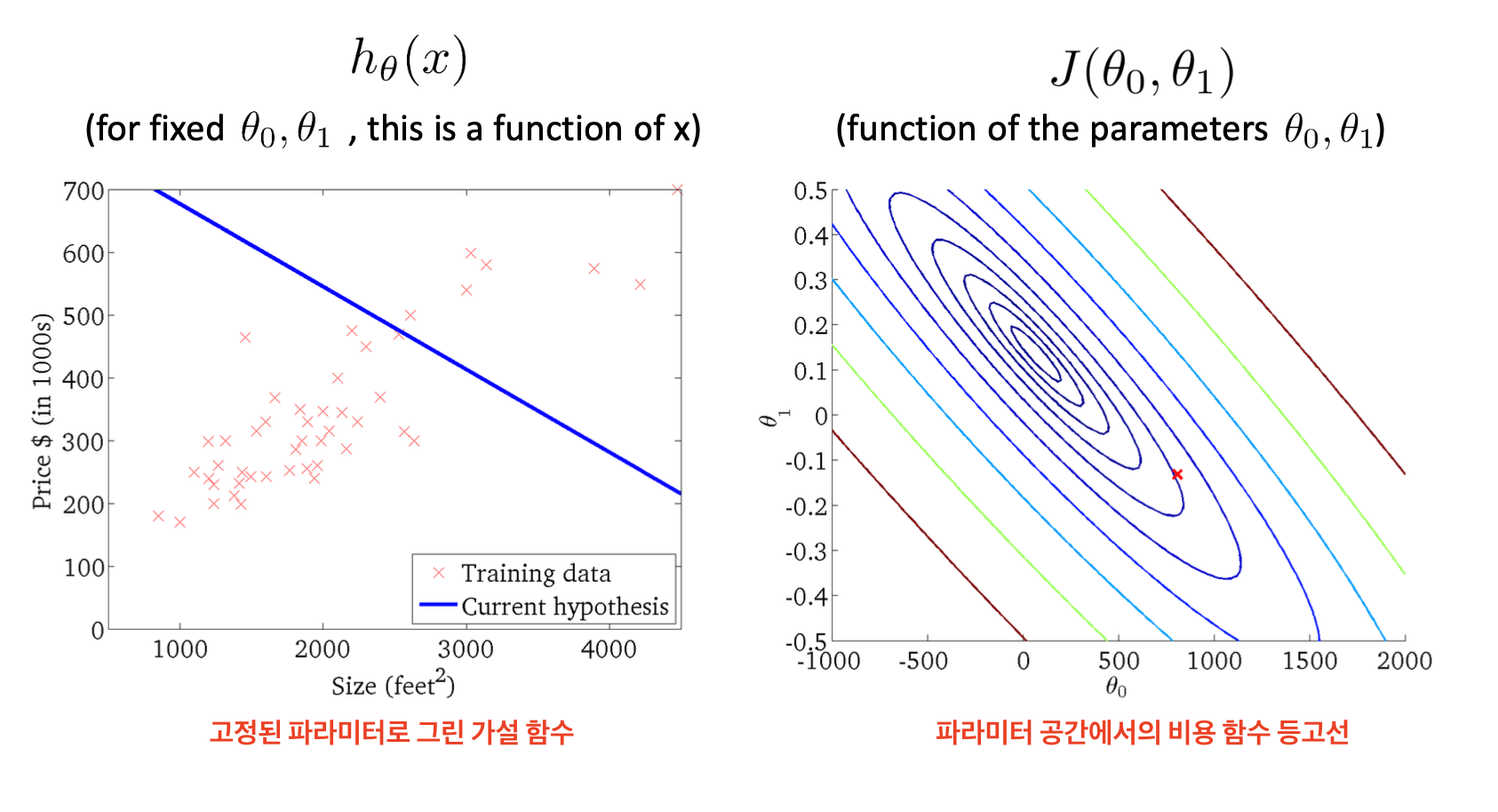
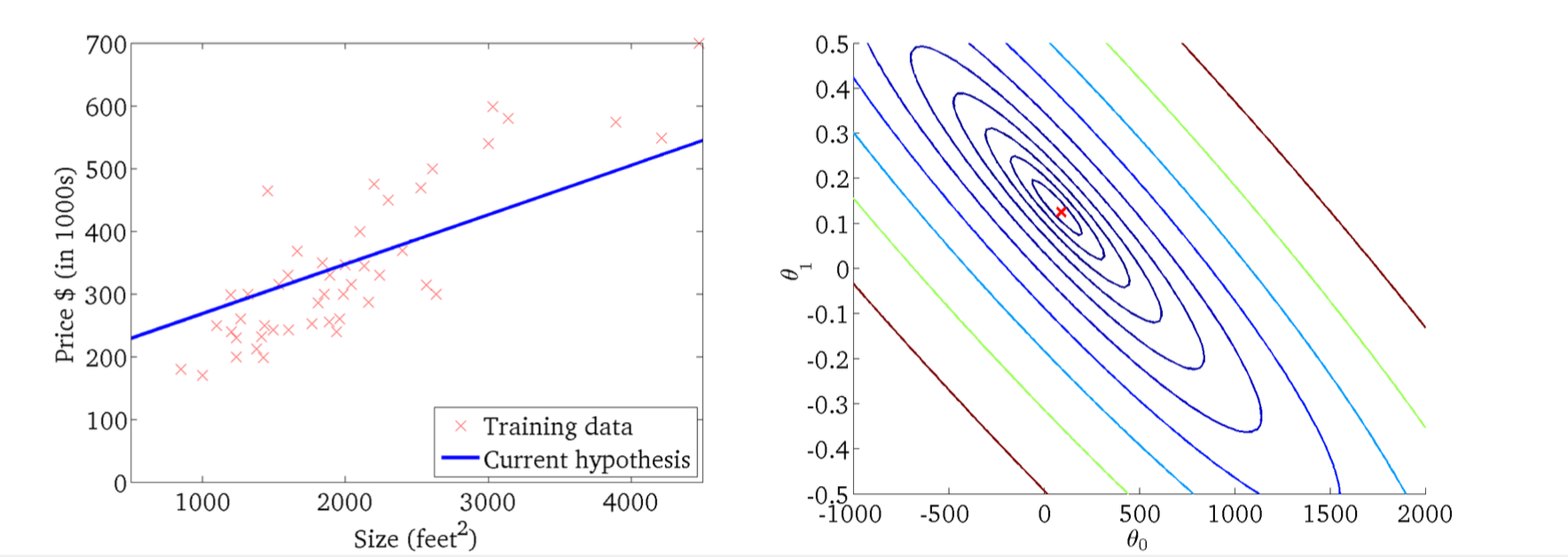
파라미터 공간에서의 비용 함수 등고선
가로축은 절편 θ0, 세로축은 기울기 θ1
안쪽(진한 파랑)일수록 cost가 작고, 바깥(빨강)일수록 cost 큼
Optimization - Matrix representation in data
데이터 행렬 X
각 행 [1,x1(i),x2(i),…,xd(i)] 은 i번째 샘플의 feature 벡터
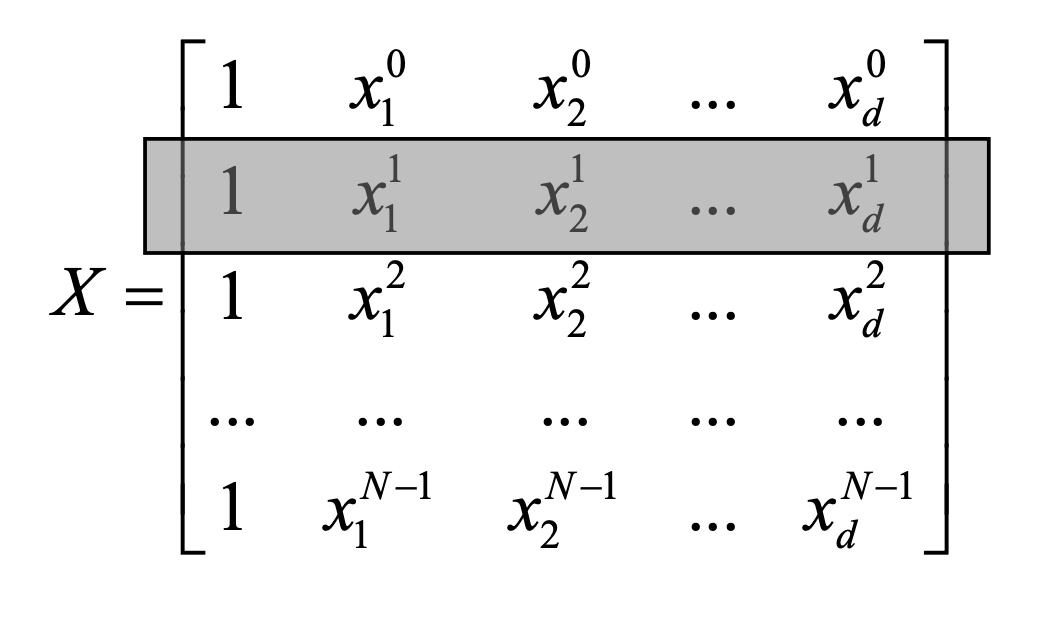
타겟 벡터 y∈RN
y=[y(1),y(2),…,y(N)]T
가중치 벡터 θ∈Rd+1
θ=[θ0,θ1,…,θd]T
모든 샘플에 대한 총 제곱 오차
∥y−Xθ∥22
Optimization - Getting a solution 𝜽
선형 회귀의 최적 파라미터 θ∗를 얻는 방법
- 정규 방정식(Normal Equation)
- 경사 하강법(Gradient Descent)
훈련 데이터에 대한 MSE = E(θ)
최적의 θ∗는
θ∗=θ∈Rd+1argminE(θ)=θargmin2N1∥Xθ−y∥22
이차(Quadratic) 형태의 E(θ)
E(θ) 식을 전개하면,
∥Xθ−y∥22=(Xθ−y)T(Xθ−y)
=((Xθ)T−yT)(Xθ−y)
=(θTXT−yT)(Xθ−y)
E(θ)=2N1(θTXTXθ−2θTXTy+yTy)
연속적이고
미분 가능하며
볼록(convex)한 이차 함수(quadratic form)
정규 방정식(Normal Equation)과 경사 하강법(Gradient Descent)

Normal equation (Least Square) - Analytic solution of 𝜽
정규 방정식 : 손실 함수를 0으로 만드는 해를 직접 구하는 수학적 방법
도함수를 0으로 놓기
이차 형태이므로, θ에 대한 기울기(gradient)를 구하고
0으로 만들면 전역 최솟값의 조건
∇θE(θ)=N1(XTXθ−XTy)=0
정규 방정식 얻기
θ∗=(XTX)−1XTy
한계점
고차원·빅데이터에서는 XTX의
생성·역행렬 계산이 불가능하거나 너무 느림
→ 정규 방정식 대신 경사 하강법 (반복 최적화 알고리즘) 사용
Gradient descent algorithm
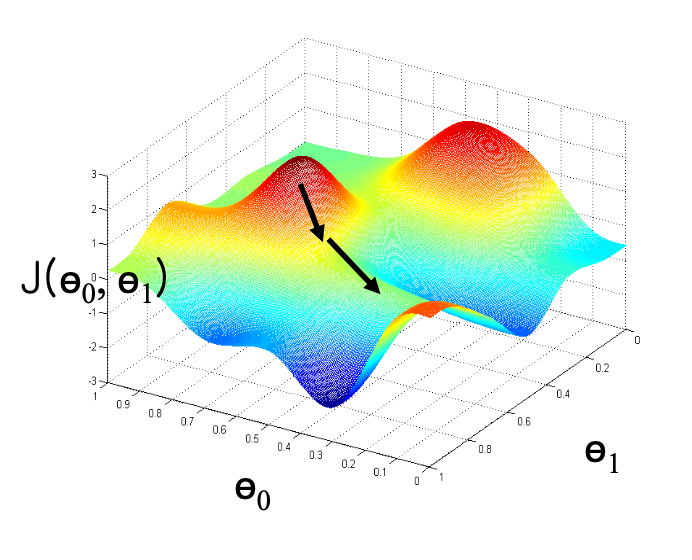
정규 방정식처럼 한 번에 해를 직접 구하는 대신,
반복(iterative)적으로 모델 파라미터 θ를 조금씩 갱신해 가면서
손실 함수 J(θ)를 최소화하는 방법
방향 결정
기울기(gradient) ∇J(θ) : 손실이 가장 빠르게 증가하는 방향을 가리킴
→ 손실을 감소시키려면, 기울기의 반대 방향으로 이동
J(θ) : 파라미터(가중치) θ에 대한 손실 함수
θnew←θold−α∂θ∂J(θ)
학습률(learning rate)
학습률 α : 매 스텝마다 파라미터를 얼마나 멀리 옮길지를 조절
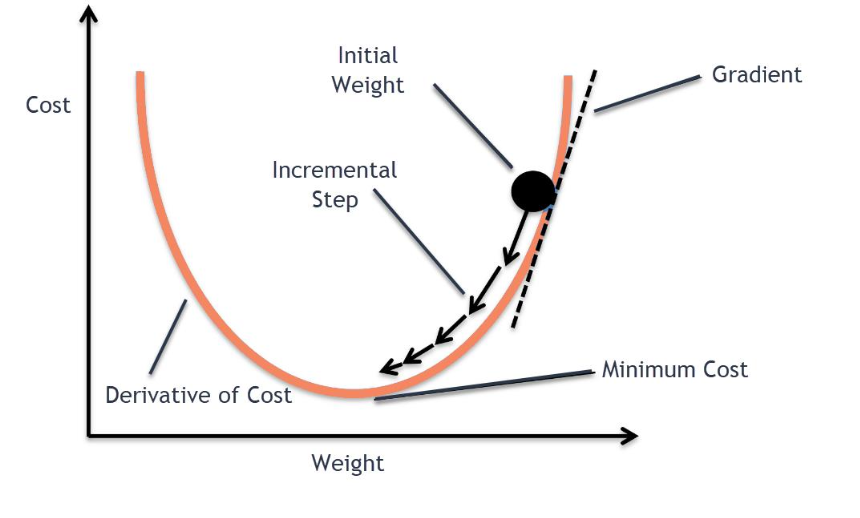
Illustration: Error surface
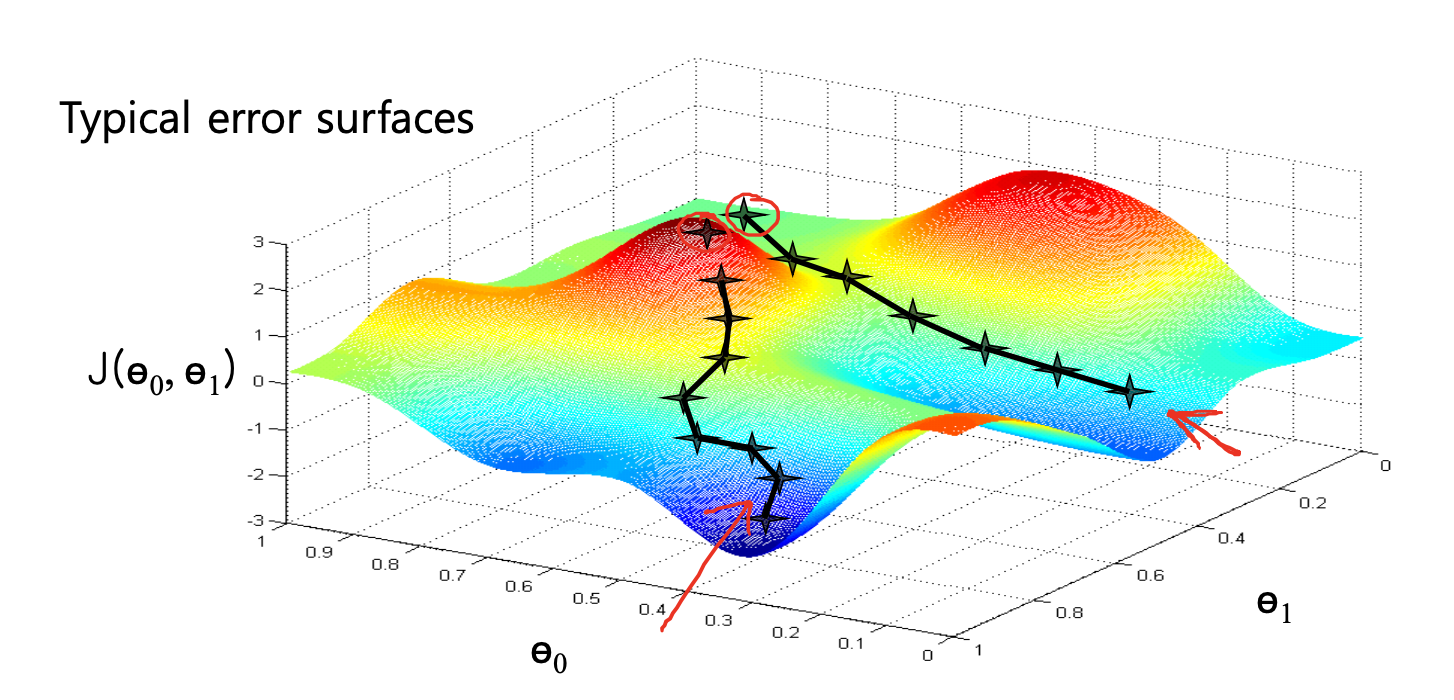
전역 최솟값(global minimum) 이 아니라,
시작 지점에서 가장 가까운 국소 최솟값(local minimum) 으로 수렴할 수 있음
→ 초기 θ 값(initial position)을 어디로 잡느냐에 따라 달라짐
Gradient descent algorithm for linear regression
모델과 손실 함수
모델
hθ(x)=θ0+θ1x
손실 함수 (MSE)
J(θ0,θ1)=2m1i=1∑m(hθ(x(i))−y(i))2
가중치(파라미터)별 기울기(편미분)
∂θ0∂J=m1i=1∑m(hθ(x(i))−y(i))
∂θ1∂J=m1i=1∑m(hθ(x(i))−y(i))x(i)
경사 하강법 업데이트 식
θ0:=θ0−αm1i=1∑m(hθ(x(i))−y(i))
θ1:=θ1−αm1i=1∑m(hθ(x(i))−y(i))⋅x(i)
Gradient descent algorithm VS Normal equation
