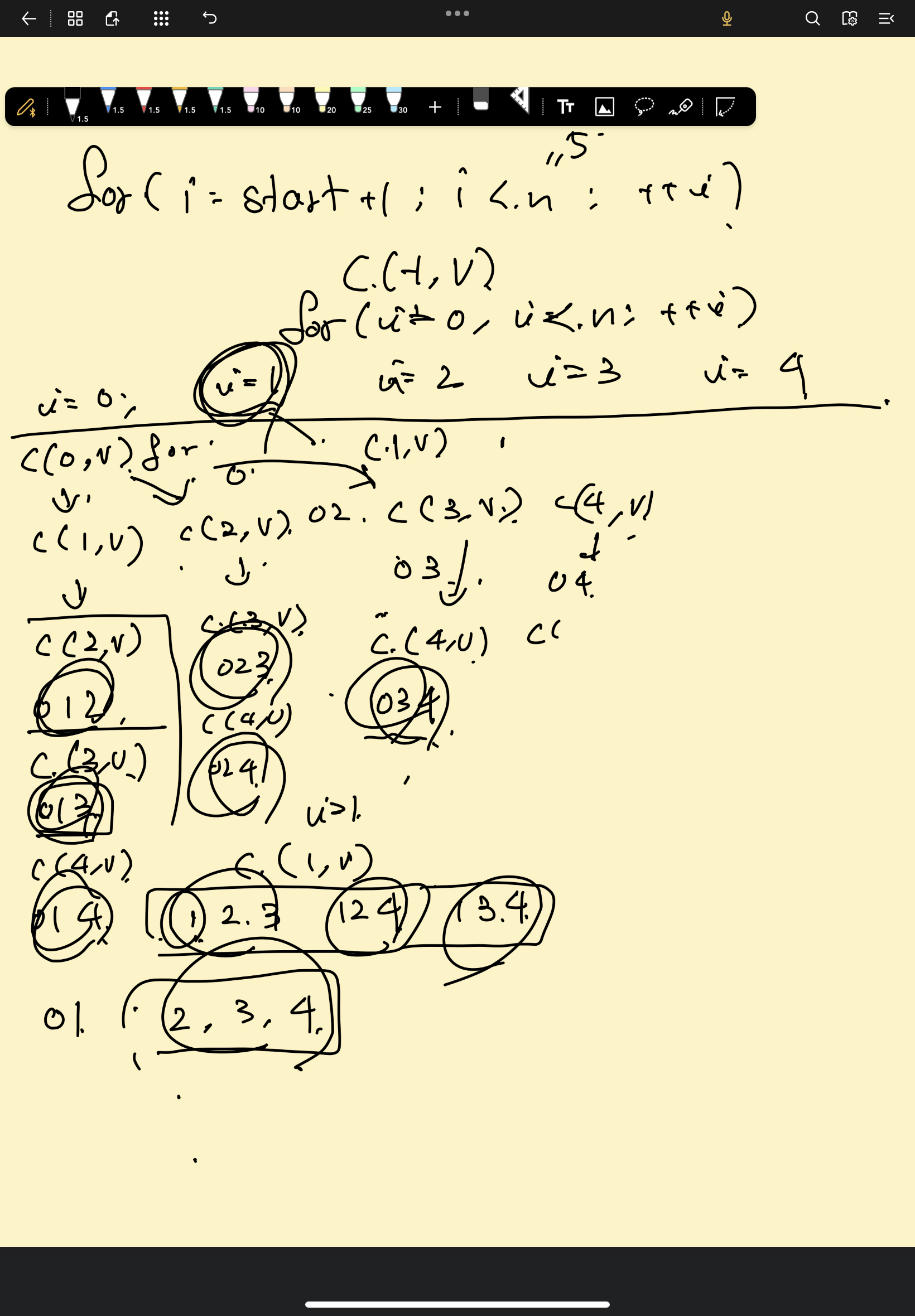아래 부분도 Permutation "순열" 코드이다.

아래의 경우에는 algorithm 헤더파일에 있는
next_permutation을 사용한 순열 구현이다.

순열 (재귀함수)

재귀 함수를 통해서 "순열"을 구해볼 것이다.

아래의 코드처럼 구해주면 되는데 "도식화"를 한두번쯤은 해보길 바란다. 해보셈!

n P r = n! / (n - r)!

void MakePermutation(int n, int r, int d)
{
	cout << n << " : " << r << " : " << d << endl;

	if (r == d)
	{
		Printf(v);
		return;
	}

	for (int i = d; i < n; ++i)
	{
		std::swap(v[i], v[d]);
		MakePermutation(n, r, d + 1);
		std::swap(v[i], v[d]);
	}
}

int main()
{	
	v.push_back(1);
	v.push_back(2);
	v.push_back(3);
	
	MakePermutation(3, 3, 0);
    
	return 0;
}

중간에 swap하고 mp -> swap하는 과정에서 다시 원상복구됨.

조합

순열은 순서와 상관있이 뭔가를 뽑는 것이고

조합은 "순서와 상관없이" 뭔가를 뽑는 경우의 수이다.

반복문으로도 조합 구현할 수 있는데
만약 n C r에서 n이 3개 라면은 3중for문 필요하고 4라면은 4중 for문이 필요하기 때문에
재귀로 이해를 하고 있는 것이 좋을거같다.

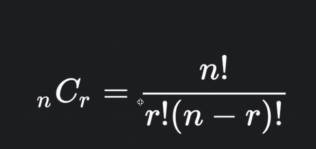
재귀로 조합 구현 ❗❗❗

int k = 3;
int n = 5;
int arr[5] = { 1, 2, 3, 4, 5 };
void combie(int start, vector<int> v)
{
	if (v.size() == k)
	{
		Print(v);
		return;
	}

	for (int i = start + 1; i < n; ++i)
	{
		v.push_back(i);
		combie(i, v);
		v.pop_back();
	}
	return;
}


int main()
{
	vector<int> v;
	combie(-1, v);
	
	return 0;
}

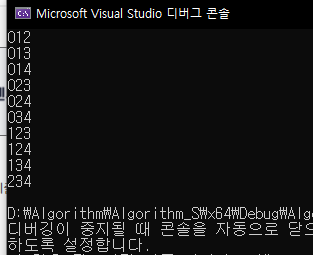
잘나오는데 코드가 이해가 안된다면은 "도식화"를 하도록 하자.

반복문으로 조합구현

반복문은 ㅎㅌㅊ인거같다...

for (int i = 0; i < n; ++i)
	for (int j = 0; j < i; ++j)
		for (int k = 0; k < j; ++k)
			cout << i << j << k << endl;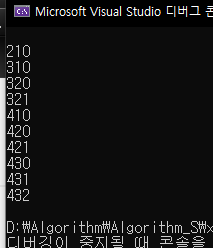

Split

c++ STL에서는 split함수 지원을 안한다.

그래서 구현을 해서 사용해야함.

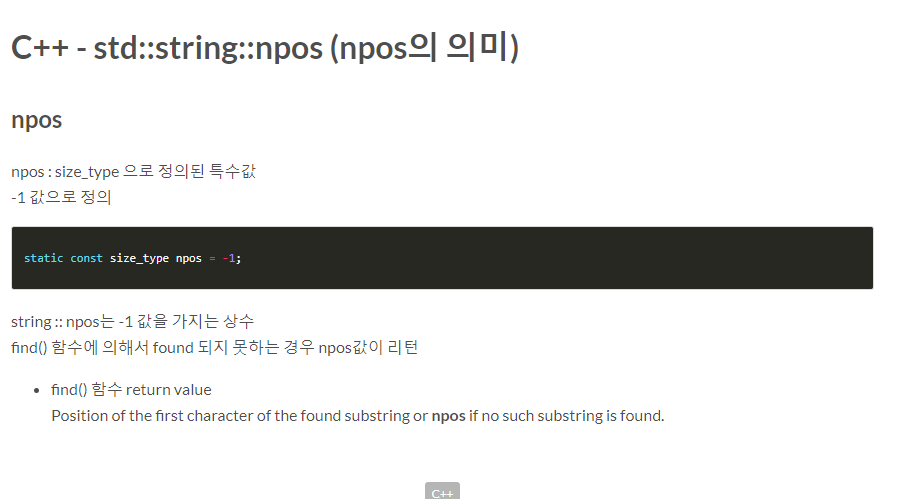
string::npos

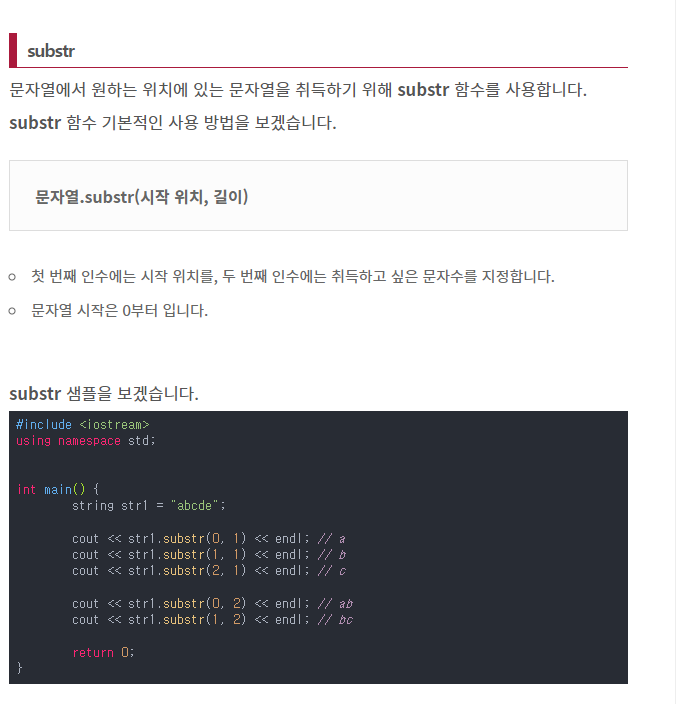
substr

https://ponyozzang.tistory.com/676

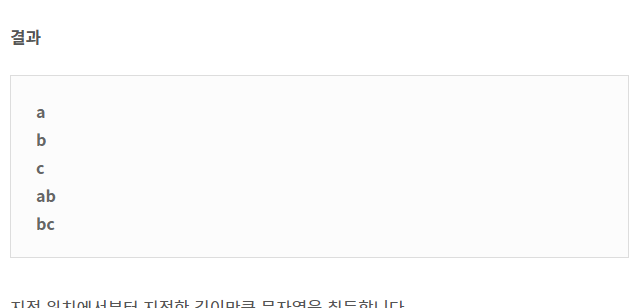
ㅇㅇ. 햇갈린다면 또 구글링 ㄱㄱ.

vector<string> split(string input, string delimiter)
{
	vector<string> ret;
	long long pos = 0;
	string token = "";
	while ((pos = input.find(delimiter)) != string::npos)
	{
		token = input.substr(0, pos);
		ret.push_back(token);
		input.erase(0, pos + delimiter.length());
	}
	ret.push_back(input);
	return ret;
}


int main()
{
	string str = "sex sex sex Hello!!!";
	vector<string> a = split(str, "x");
	
	for (string c : a) cout << c;

	return 0;
}

일단 코드보고 이해를 한다면 좋을거같다.

구글링해도 비슷비슷한듯?