
Minimum spanning Tree
최소 스패닝 트리
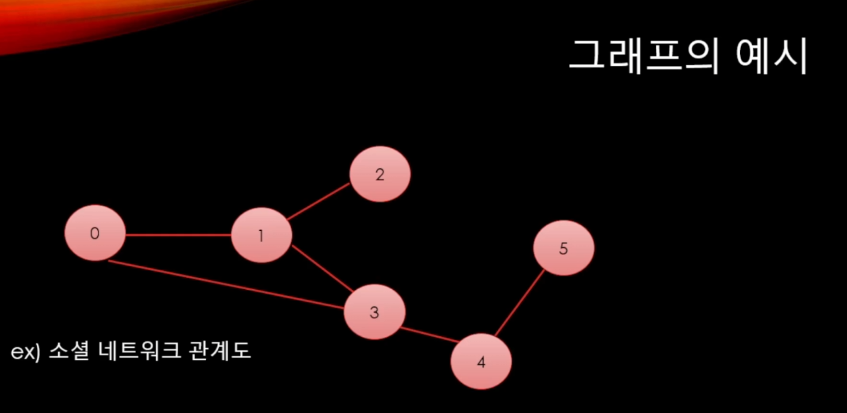
트리는 일단 노드와 간선으로 이루어져 있다.
최소 스패닝 트리란? 간선을 최소화 해서 모든 노드들을 연결하는 것을 말한다.
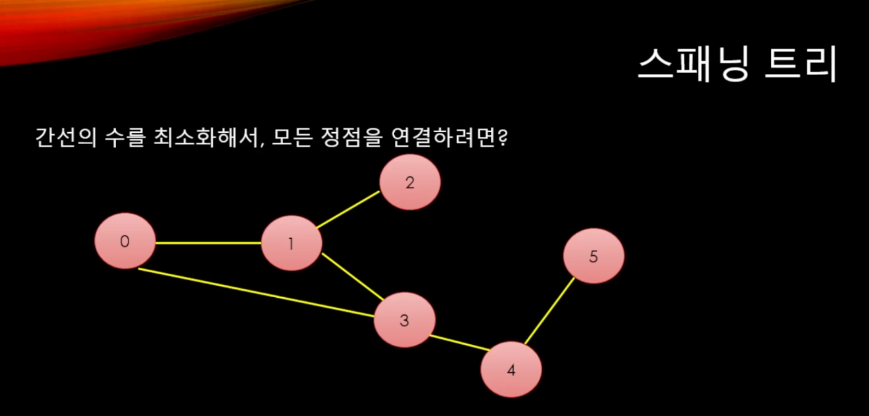
길을 연결하는 과정부터 생각을 해볼 것이다.
스패닝 트리
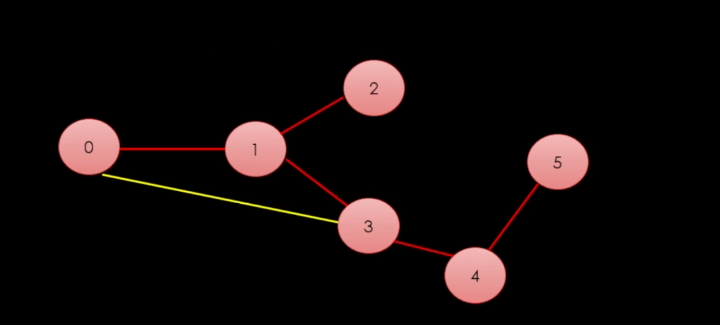
이렇게 빨간 간선으로 만 연결할 때 간선이 최소화가 된다.
간선을 최소화 한다는 말은 "사이클"이 생기면 안된다는 말이다.
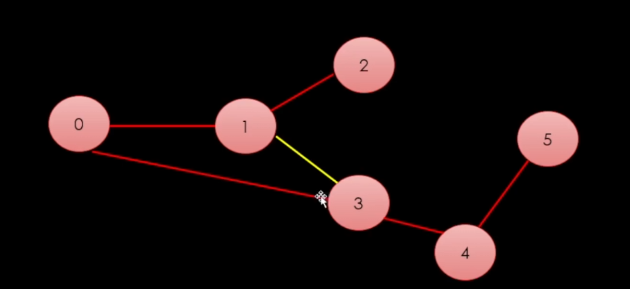
이것도 스패닝 트리라고도 볼 수 있다.
(여러가지가 존재함)
N개의 정점이 있을 경우 N-1개의 간선으로 연결이 가능함.
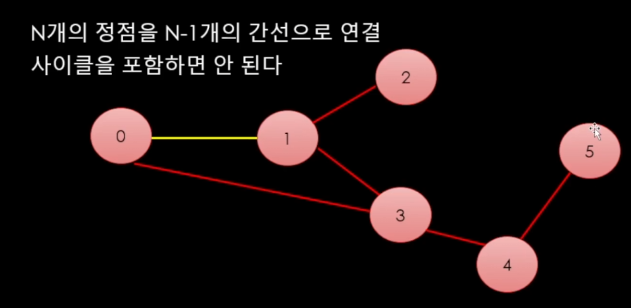
예시
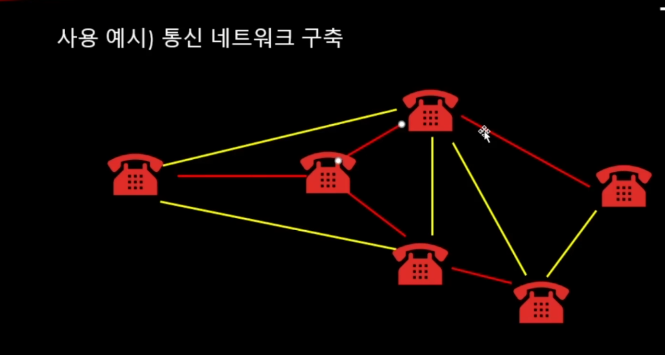
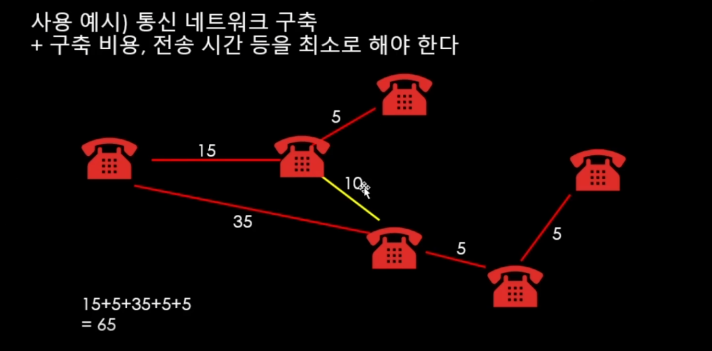
어떤 간선으로 연결을 해야 가중치가 가장 작은지 봐야함.

사이클이 발생하면 안되고, 모든 경로들에 대해서 모든 정점들에 대해서 어떤식으로든 연결이 되어있어야함.
Kruskal
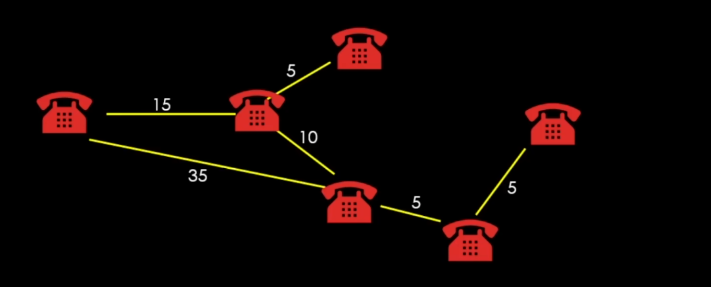
이 상황에 대해서 길을 선택을 해서 길을 만들어주어야한다고 할 때 => 최소 스패닝 트리를 만들어 주어야할 경우.
여기서 가장 대표적인 알고리즘들 중에 대표적인 애가 Kruskal 알고리즘이 있다.
Kruskal은 탐욕적인(greedy) 방법을 이용을 한다.
=>
지금 이순간에 최적인 답을 선택하여 결과를 도출 하는 방법이다.
직관을 사용하는 것 처럼 모든 경로를 다 본다음에 가장 작은 부분부터 본다.
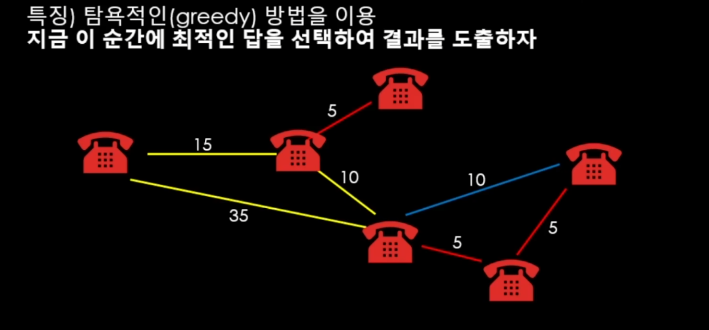
하지만 중간에 사이클이 발생하는지 안하는지도 이중으로 확인을 해주어야한다.
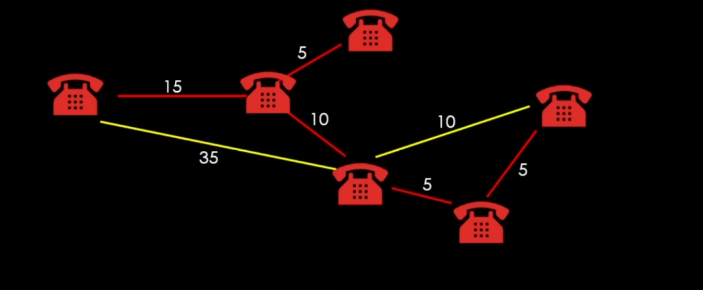
이렇게 연결이 됨.
Cycle이 생기는지 아닌지?
확인하는 방법은 모든 단위를 다 "그룹"단위로 관리를 하는 것이다.
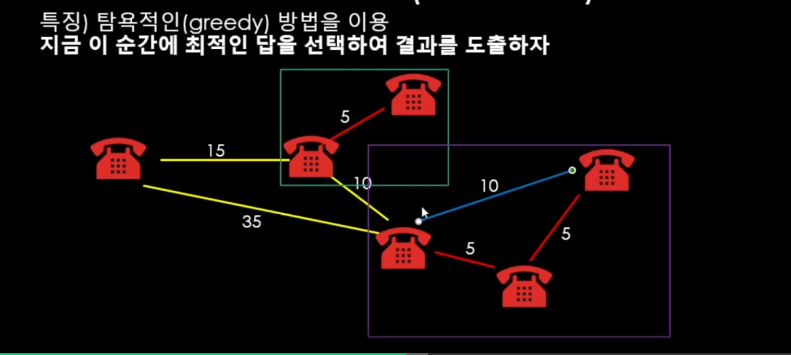
즉, 각기 다른 그룹 끼리만 연결할 수 있도록 하면된다.
그러고 나면
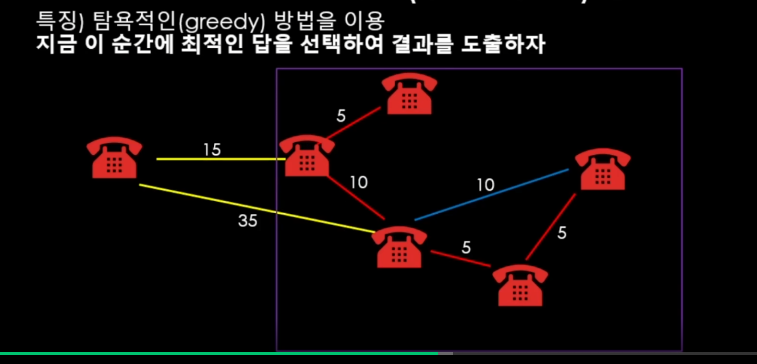
이렇게 그룹이 합쳐지는데...?!
바로 여기서 "DSU"바로 생각남...?
Union Find자료구조를 이용하게 되면은 그룹핑을 해서 합치는거 손쉽게 가능함.
Krulskal은 MST를 만들어주는 "알고리즘" 정도라고 생각하면 된다.
근데 Kruskal을 구현을 하면서 Astar처럼 안에서 도구 처럼 사용하면 좋은게 DSU이다.
(Disjoint Set)
CPP 코드
class DisjointSet
{
public:
DisjointSet(int n) : _parent(n), _rank(n, 1)
// std::vector's size => n
{
for (int i = 0; i < n; ++i)
{
_parent[i] = i;
}
}
// 니 대장이 누구니?
int Find(int u)
{
if (u == _parent[u])
return u;
// _parent[u] = Find(_parent[u]);
// return _parent[u];
return _parent[u] = Find(_parent[u]);
}
// u와 v를 합친다 (일단 u가 v 밑으로)
void Merge(int u, int v)
{
u = Find(u);
v = Find(v);
if (u == v)
return;
if (_rank[u] > _rank[v])
std::swap(u, v);
// rank[u] <= rank[v] 보장됨
_parent[u] = v;
if (_rank[u] == _rank[v])
++_rank[v];
}
private:
std::vector<int> _parent;
std::vector<int> _rank;
};
struct Vertex
{
// int data;
};
std::vector<Vertex> vertices_K;
std::vector<std::vector<int>> adjacent_K;
void CreateGraph_K()
{
vertices_K.resize(6);
adjacent_K = std::vector<std::vector<int>>(6, std::vector<int>(6, -1));
adjacent_K[0][1] = adjacent_K[1][0] = 15;
adjacent_K[0][3] = adjacent_K[3][0] = 35;
adjacent_K[1][2] = adjacent_K[2][1] = 5;
adjacent_K[1][3] = adjacent_K[3][1] = 10;
adjacent_K[3][4] = adjacent_K[4][3] = 5;
adjacent_K[3][5] = adjacent_K[5][3] = 10;
adjacent_K[5][4] = adjacent_K[4][5] = 5;
}
struct CostEdge
{
int cost;
int u;
int v;
bool operator < (CostEdge& other)
{
return cost < other.cost;
}
};
int Kruskal(vector<CostEdge>& selected)
{
int ret = 0;
selected.clear();
vector<CostEdge> edges;
for (int u = 0; u < adjacent_K.size(); ++u)
{
for (int v = 0; v < adjacent_K.size(); ++v)
{
if (u > v)
continue;
int cost = adjacent_K[u][v];
if (cost == -1)
continue;
edges.push_back(CostEdge{cost, u, v});
}
}
std::sort(edges.begin(), edges.end());
DisjointSet sets (vertices_K.size());
for (CostEdge& edge : edges)
{
// 같은 그룹이라면은 스킵.(안 그러면 사이클 발생)
if (sets.Find(edge.u) == sets.Find(edge.v))
continue;
// 두 그룹을 합친다
sets.Merge(edge.u, edge.v);
selected.push_back(edge);
ret += edge.cost;
}
return ret;
}
코드 분석 하고 배운 부분
중복 건너 뛰기
void CreateGraph_Kruskal()
{
vertices_Kruskal.resize(6);
adjacent_Kruskal = std::vector<std::vector<int>>(6, std::vector<int>(6, -1));
adjacent_Kruskal[0][1] = adjacent_Kruskal[1][0] = 15;
adjacent_Kruskal[0][3] = adjacent_Kruskal[3][0] = 35;
adjacent_Kruskal[1][2] = adjacent_Kruskal[2][1] = 5;
adjacent_Kruskal[1][3] = adjacent_Kruskal[3][1] = 10;
adjacent_Kruskal[3][4] = adjacent_Kruskal[4][3] = 5;
adjacent_Kruskal[3][5] = adjacent_Kruskal[5][3] = 10;
adjacent_Kruskal[5][4] = adjacent_Kruskal[4][5] = 5;
}에서 노드가 서로 연결 되도록 이렇겠 해주었는데
Kruskal 함수에서 이 부분을 edges에 넣을 때
for (int u = 0; u < adjacent_Kruskal.size(); ++u)
{
for (int v = 0; v < adjacent_Kruskal.size(); ++v)
{
if (u > v) continue; // adjacent_Kruskal 중복되는 부분 건너뛰는 코드
int cost = adjacent_Kruskal[u][v];
if (cost == -1) continue;
edges.emplace_back(CostEdge{ cost, u, v});
}
}이중 for문을 돌리기 때문에 중복될 수 있었는데
if (u > v) continue;딱 이 한줄로 중복된 부분 걸러냄.
adjacent_Kruskal[0][1] = adjacent_Kruskal[1][0] = 15;
하면 (0, 1), (1, 0) 둘다 15인데 중복 막는 부분임.
2차원 배열 공식 ❗
2차원 배열을 1차원으로 관리하고싶을 때
int32 u = edge.u.y * _size + edge.u.x;
int32 v = edge.v.y * _size + edge.v.x;edges에서는 u, v라는 노드에 대한 cost가 들어있는 struct이다.
[ 0 ][ 1 ] [ 2 ][ 3 ] ... [ 24 ] 25개
[ 25 ][ 26 ] [ 27 ][ 28 ] ... [ 49 ] 25개
