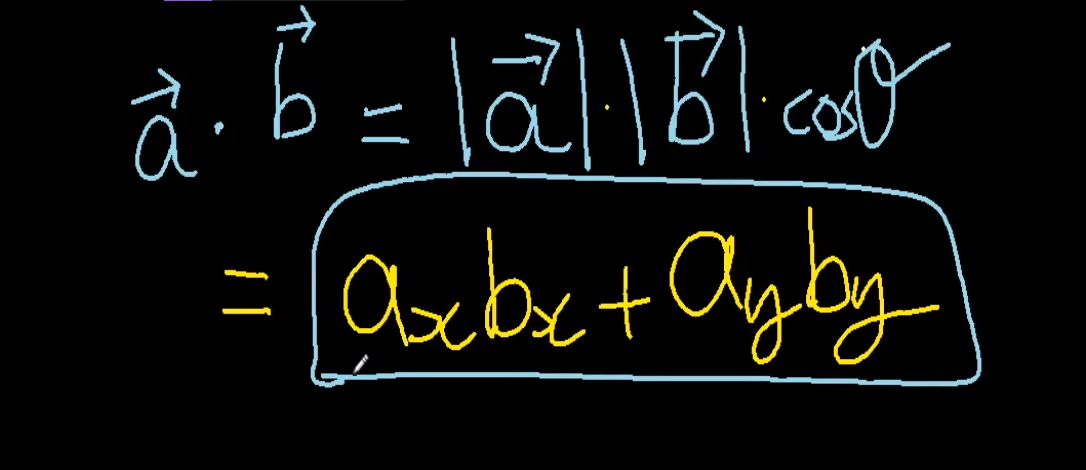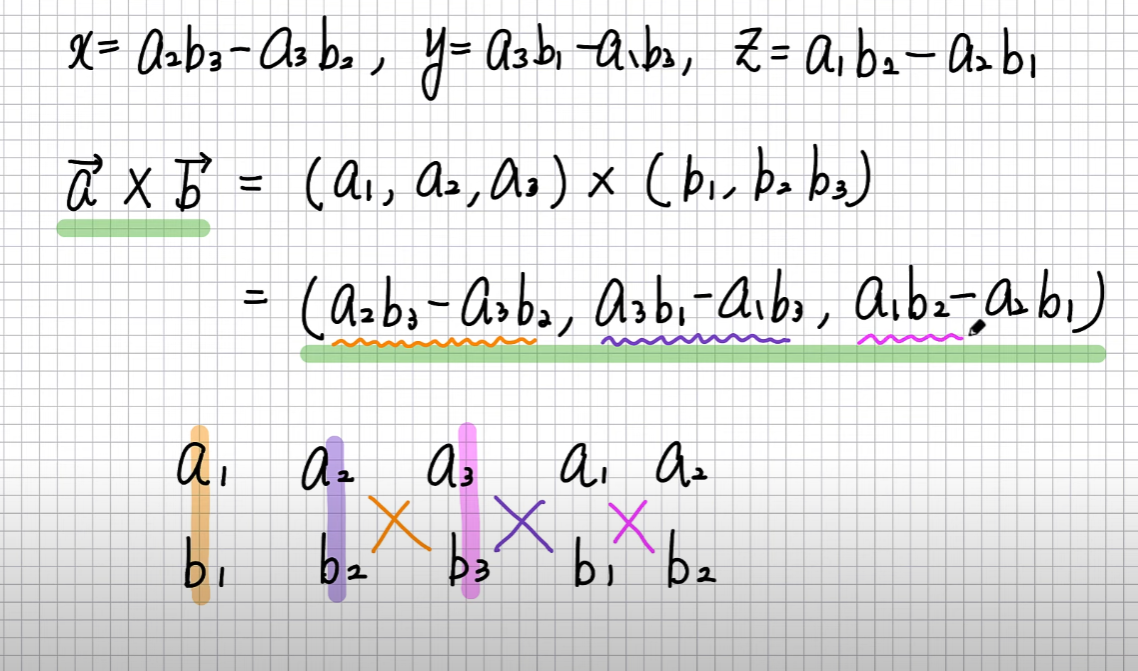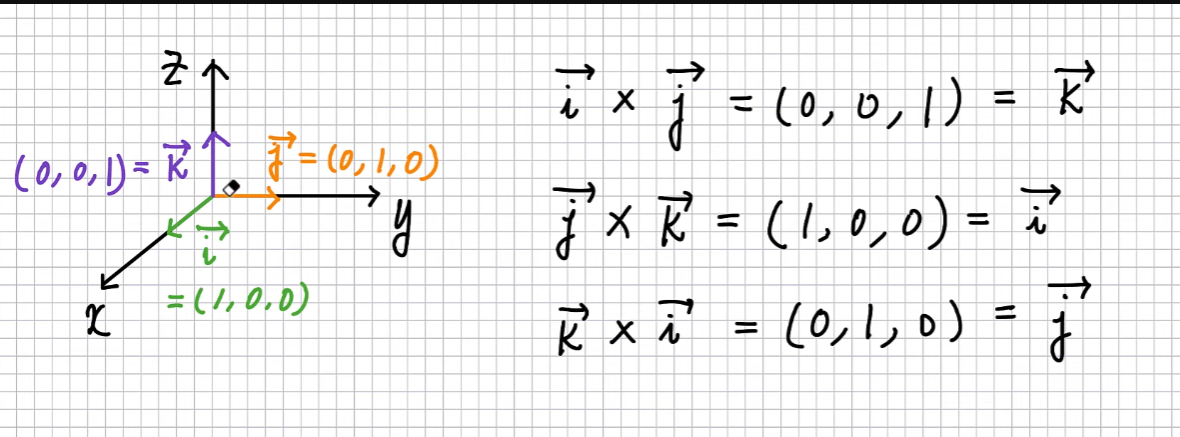삼각함수

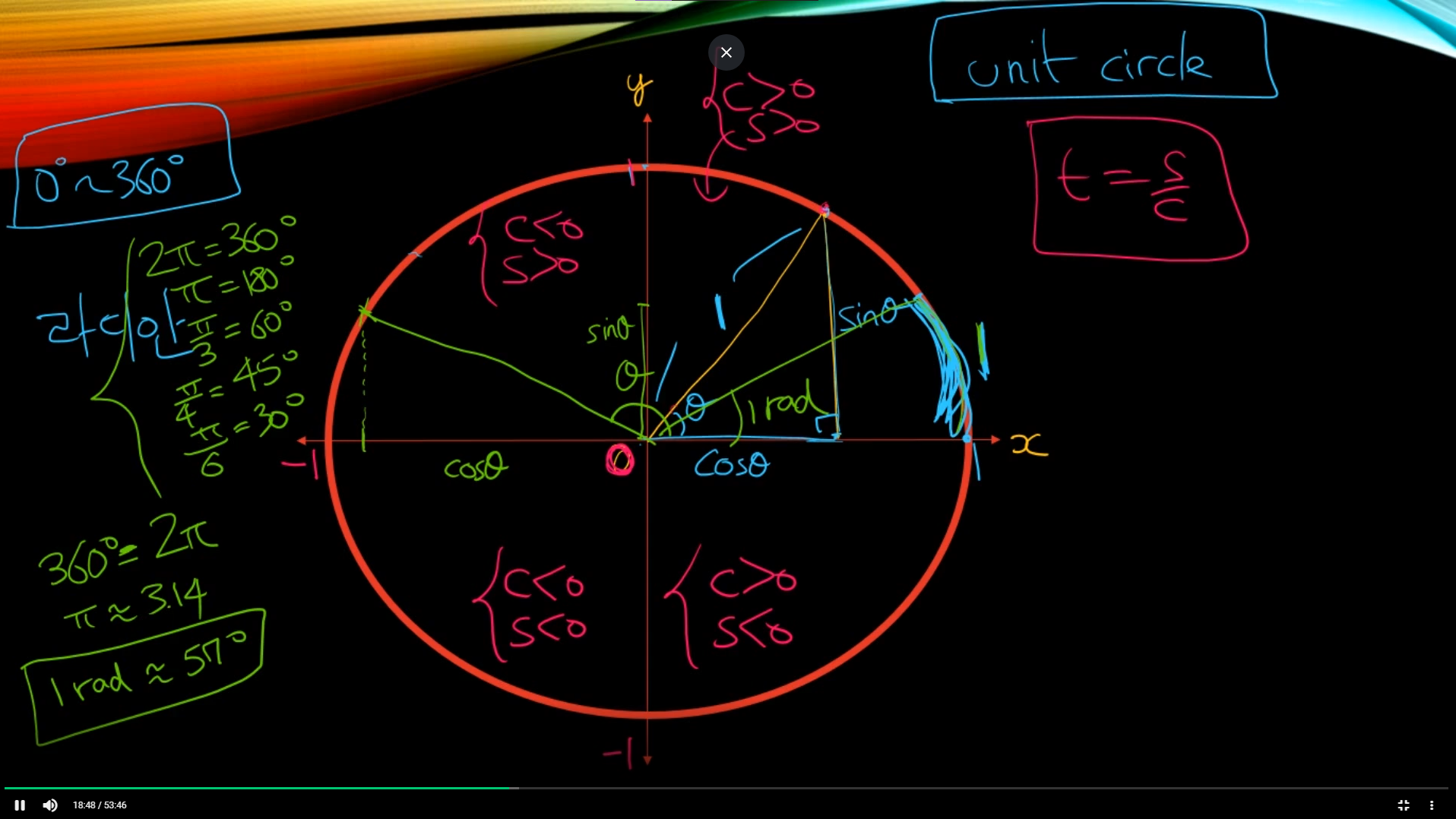
sin, cos특징이 있음

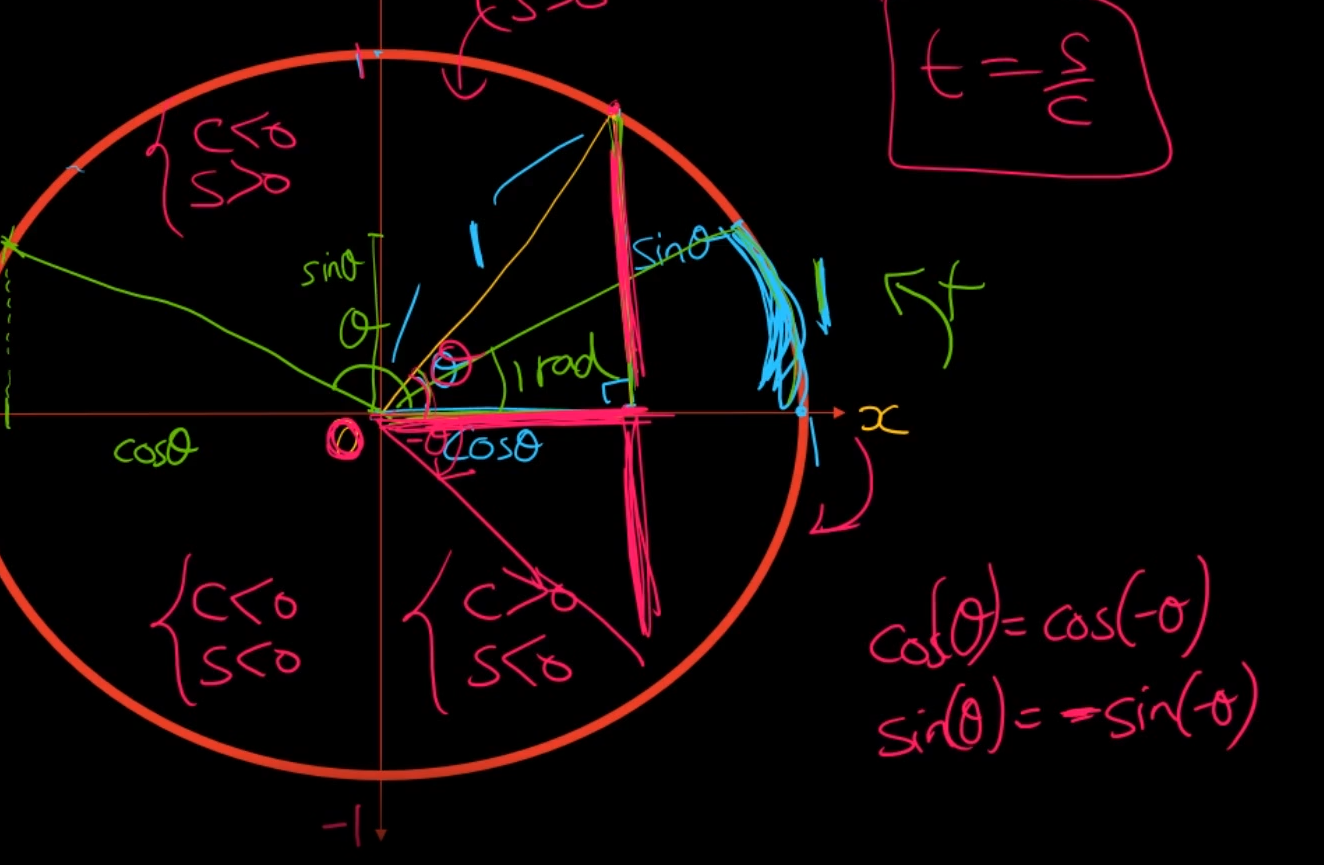
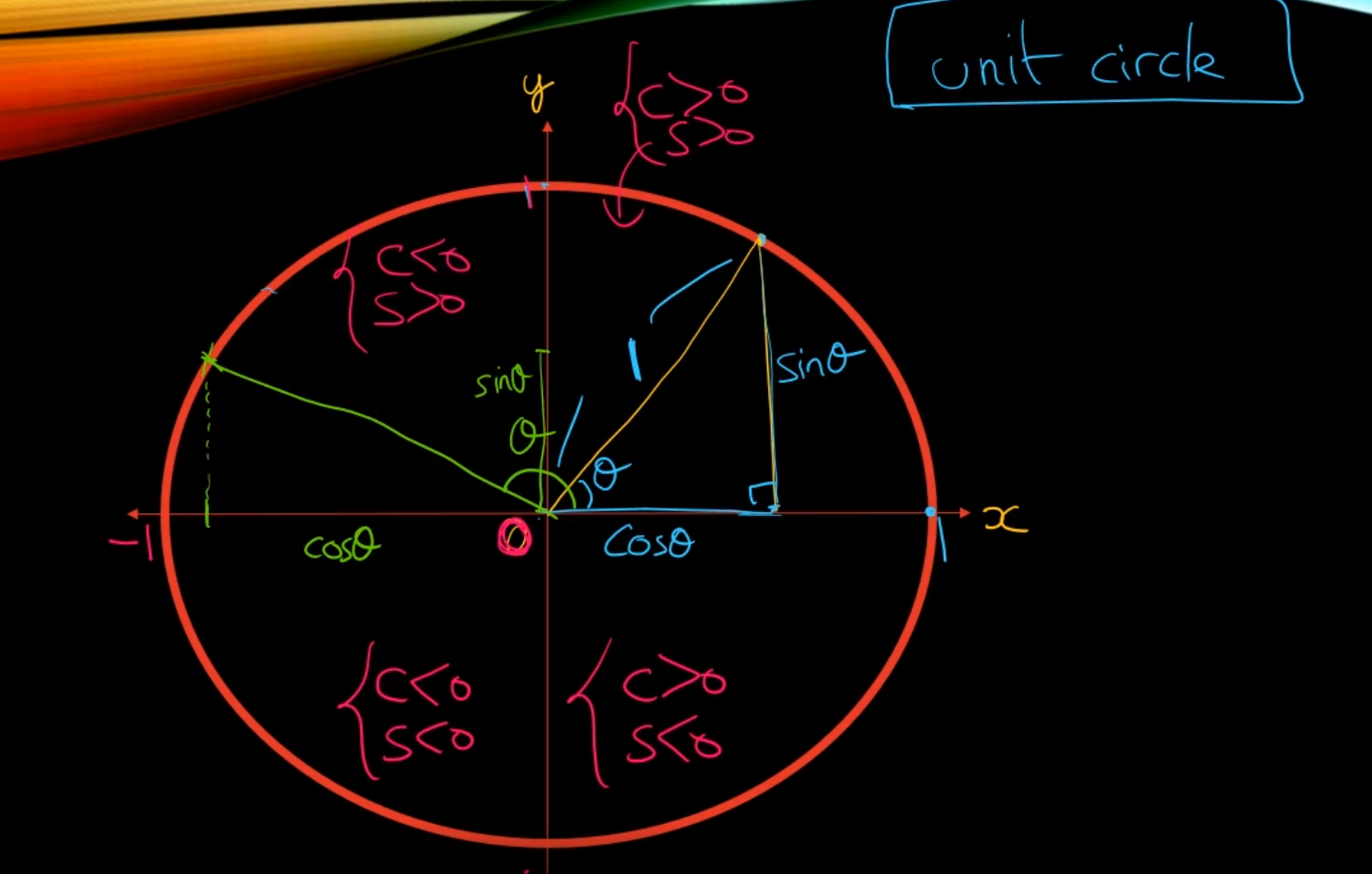
cos는 음수값이라도 똑같은데 sin은 반대임. 단위원에서 생각을 해보도록 하자.

1. 짝(우) 함수, 홀(기) 함수

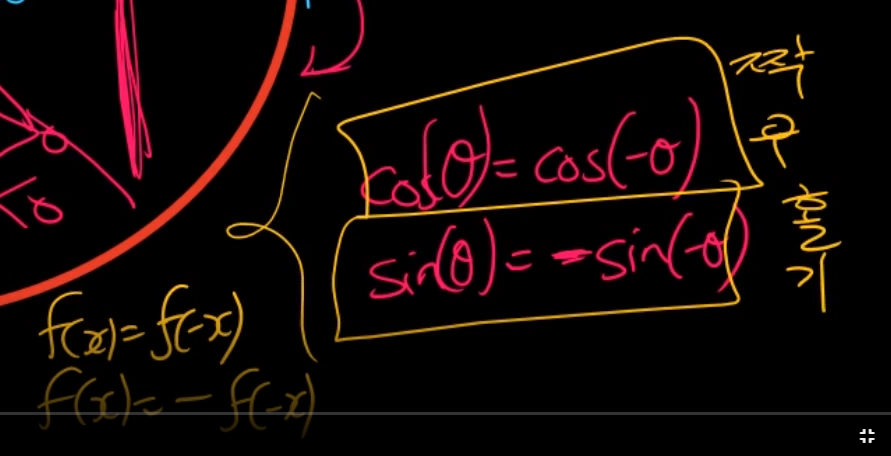
cos, sin의 중요한 성질.

2. 삼각함수의 역함수

각도를 알았을 때 비율을 알고 샆다면은 cos, sin, tan쓰는 것이고

비율을 아는 상태에서 비율에 해당하는 각도를 알고싶다면은

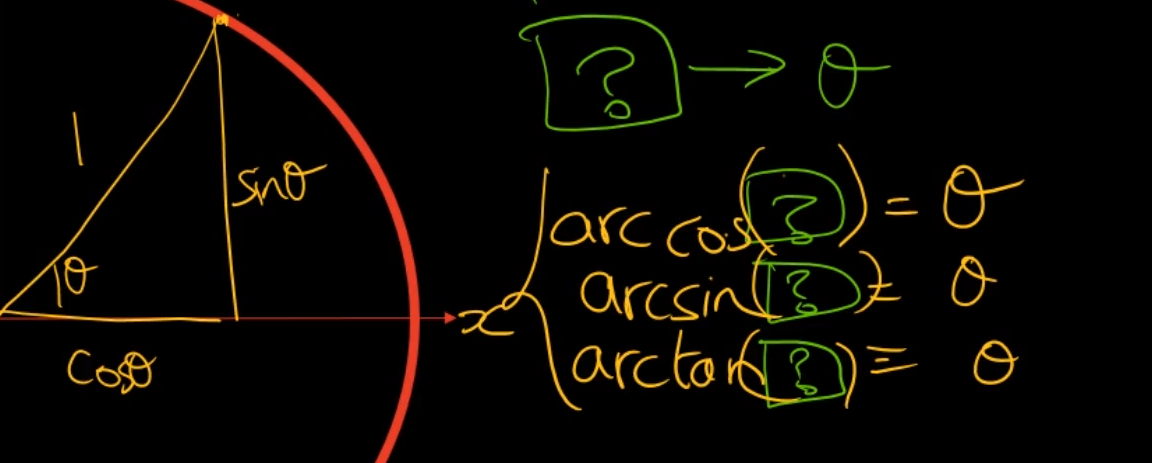
arccos, arcsin, arctan을 사용을 한다.

3. 삼각함수의 공식 ❗

• 1) cos법칙 ❗

  

  

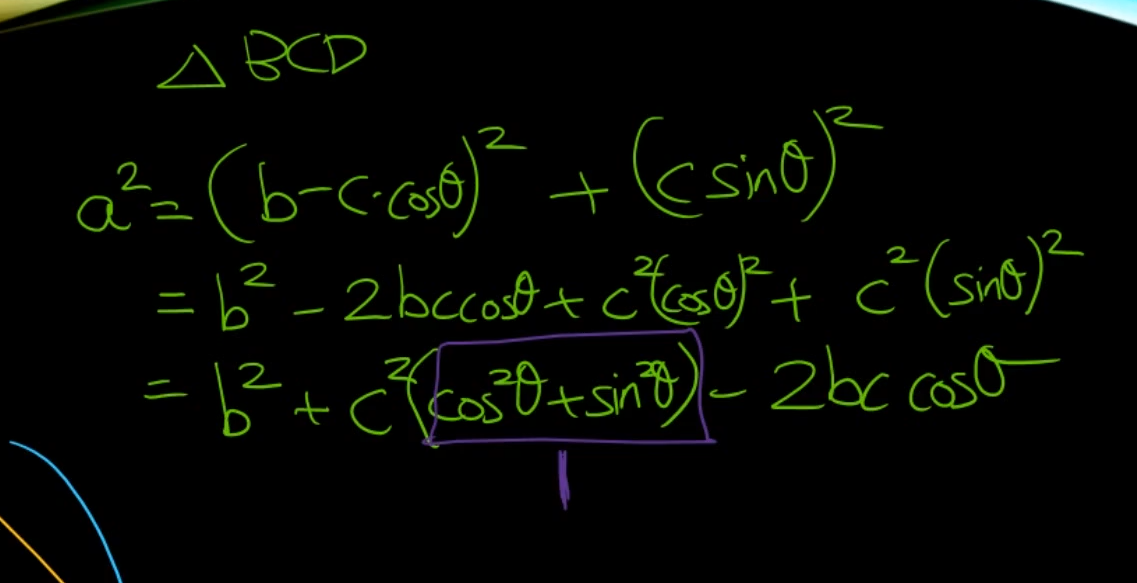
  여기서 con제곱 + sin제곱은 항상 1이다.

  
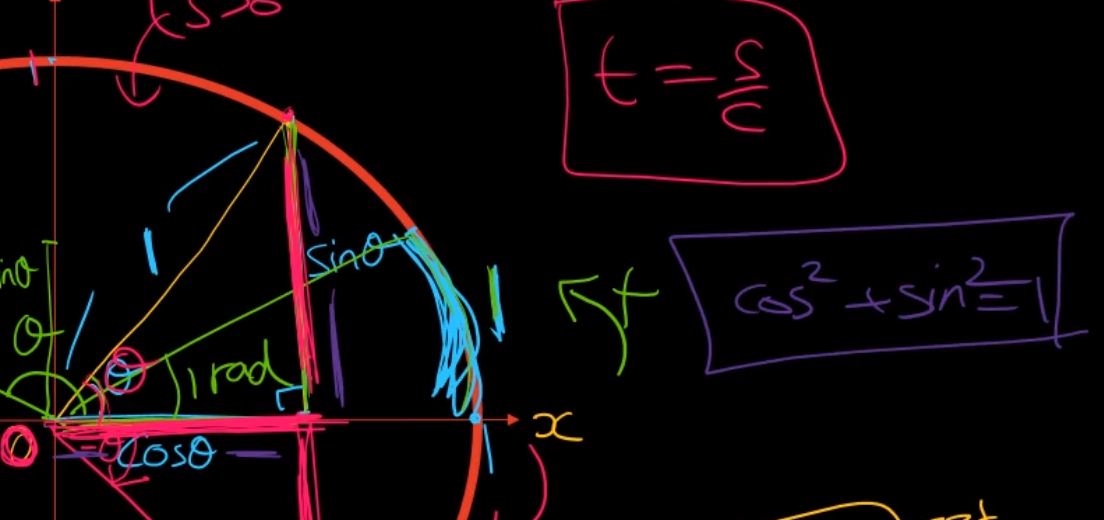
  단위원에서 생각을 해보면 1이라는 것은 cos제곱 + sin제곱이다.
  그래서 cos제곱 + sin제곱은 날라가서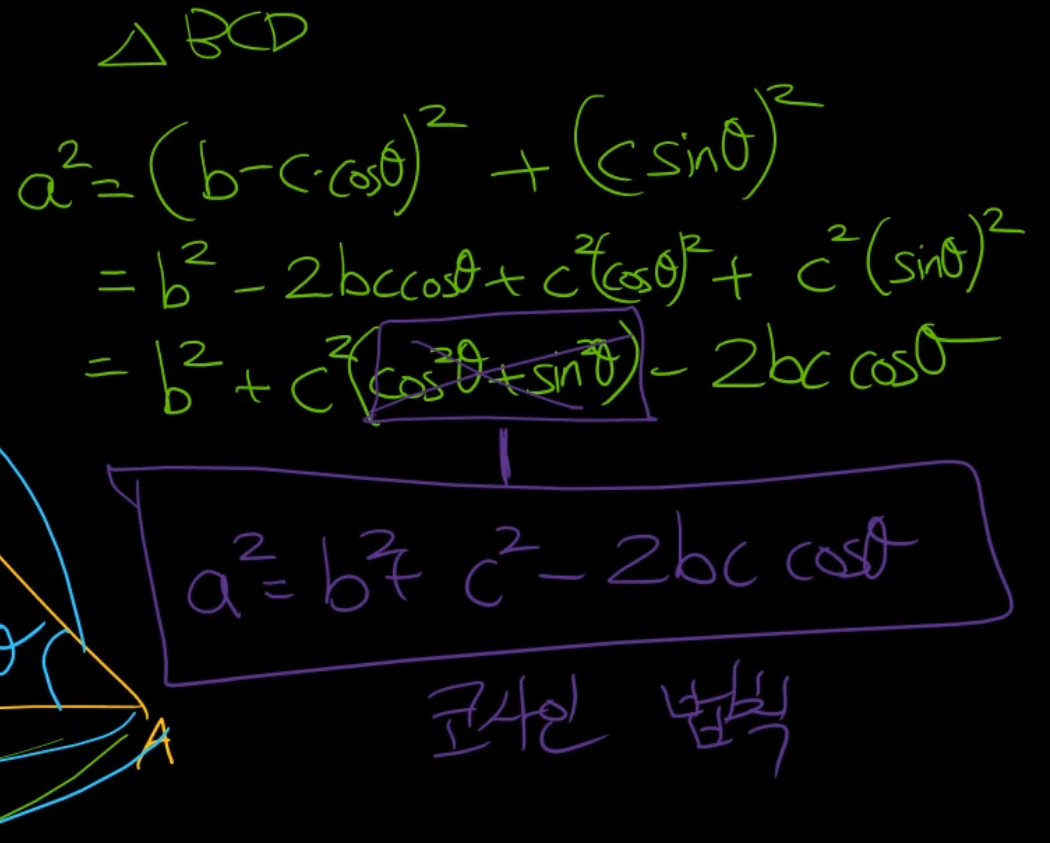

  
  이부분을 "코사인 법칙"이라고한다.

• 2) 코사인 덧셈 정리

  
  

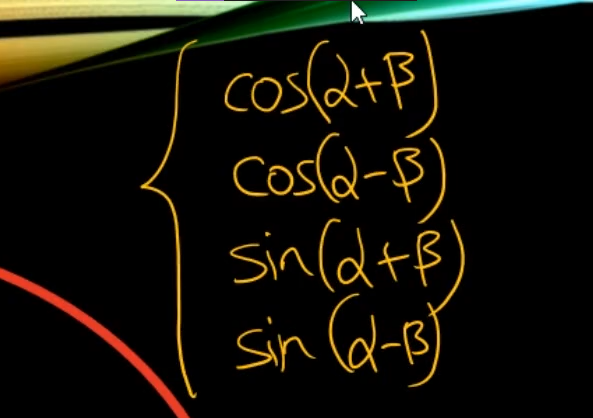
  -> 회전행렬 구할 때 필요함.

  코코사사

  
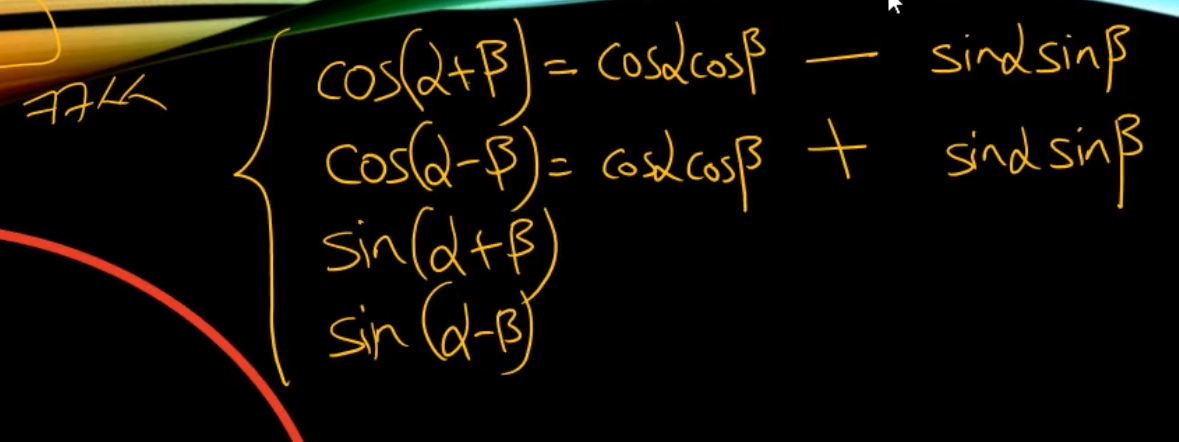
  부호만 반대로 해주면 된다.

  sin의 경우에는 사코코사

  

  
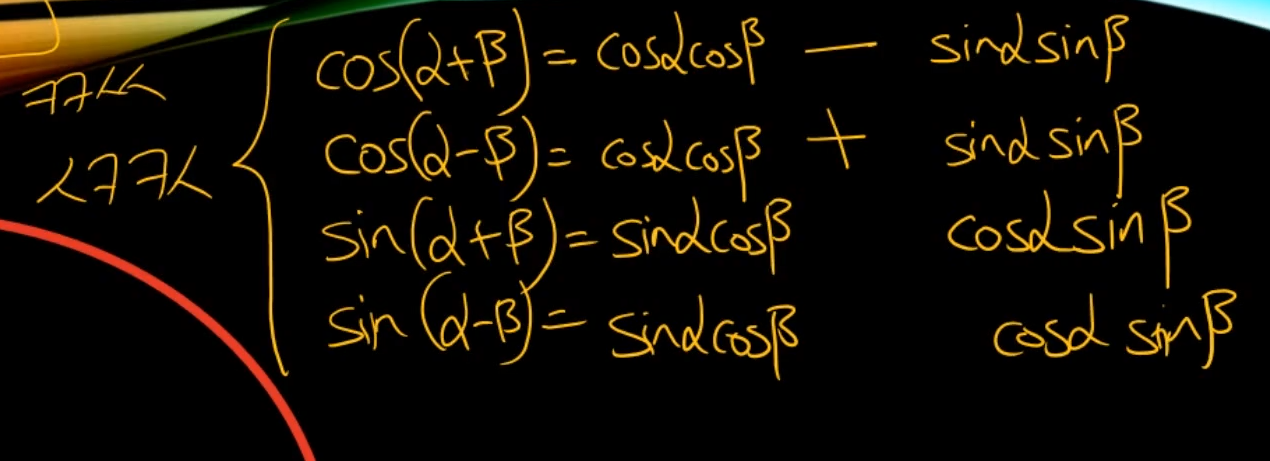
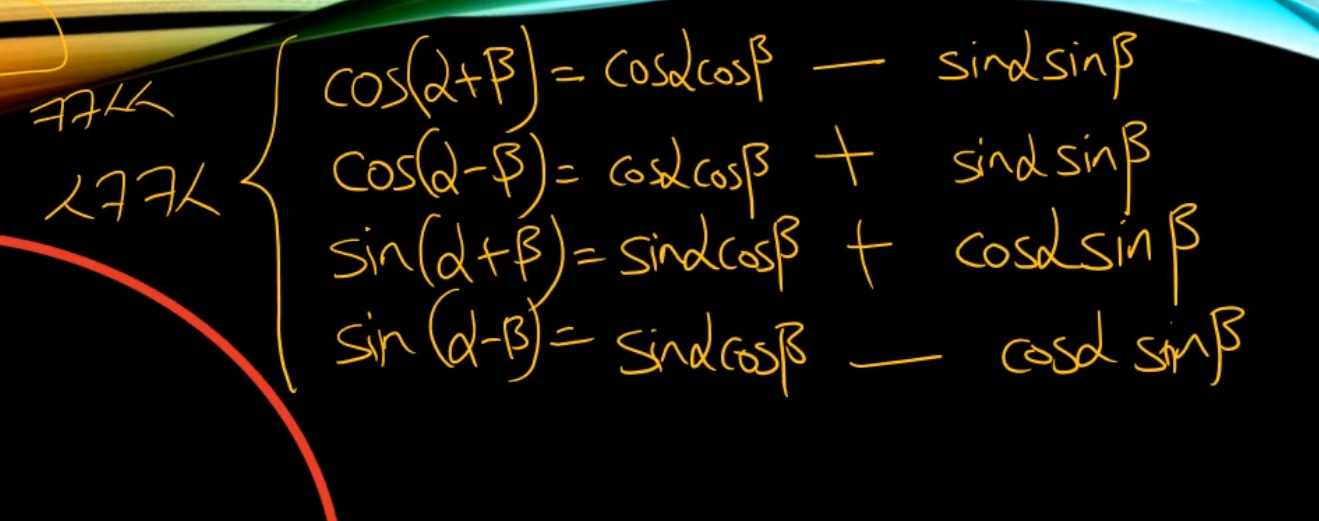
  부호는 그대로 해준다.

코사인 덧셈 정리 증명

증명방법은 많다. 오일러나 등등..

가장 직관적인 방법은 코사인 법칙 사용해서 보는 것이다.

=>

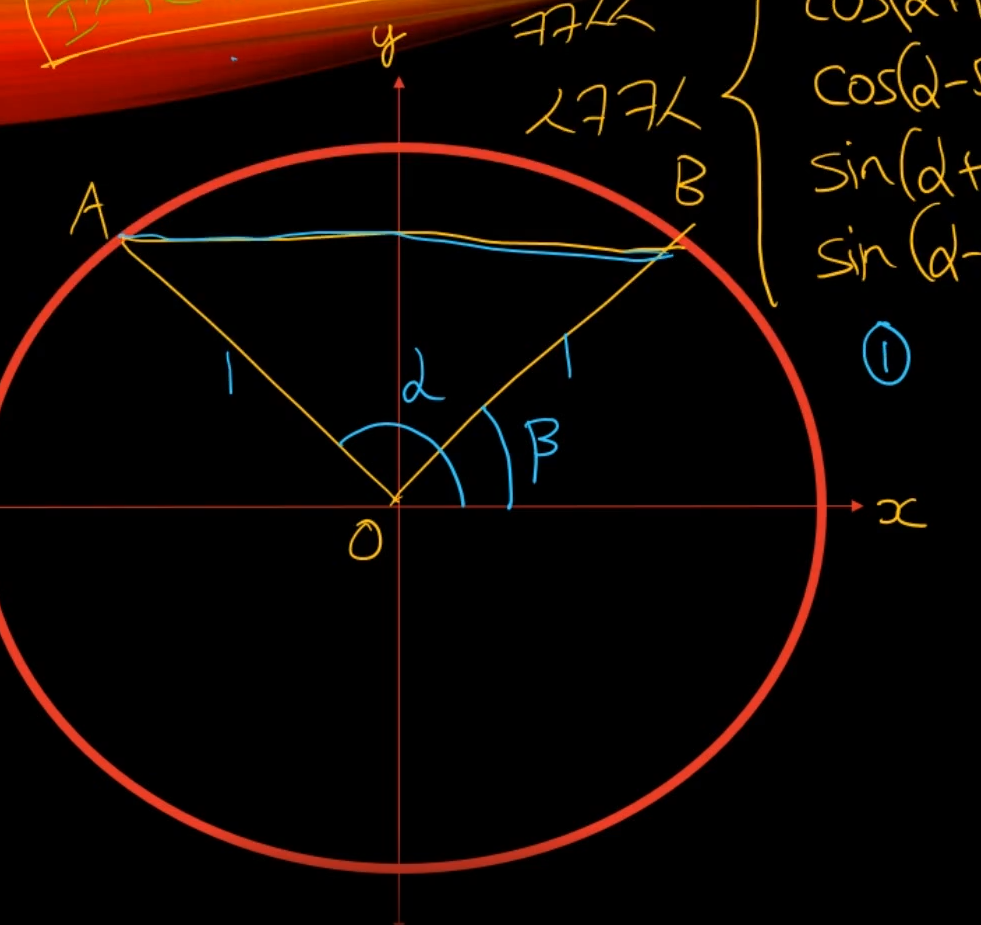
Vector

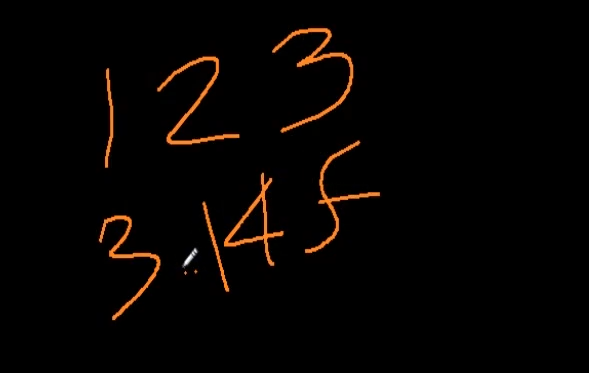
이런 고정된 숫자를 "스칼라" 라고함 => 크기 정보 전달함.

• vector

  크긱 + 방향

1. Vector기본 개념

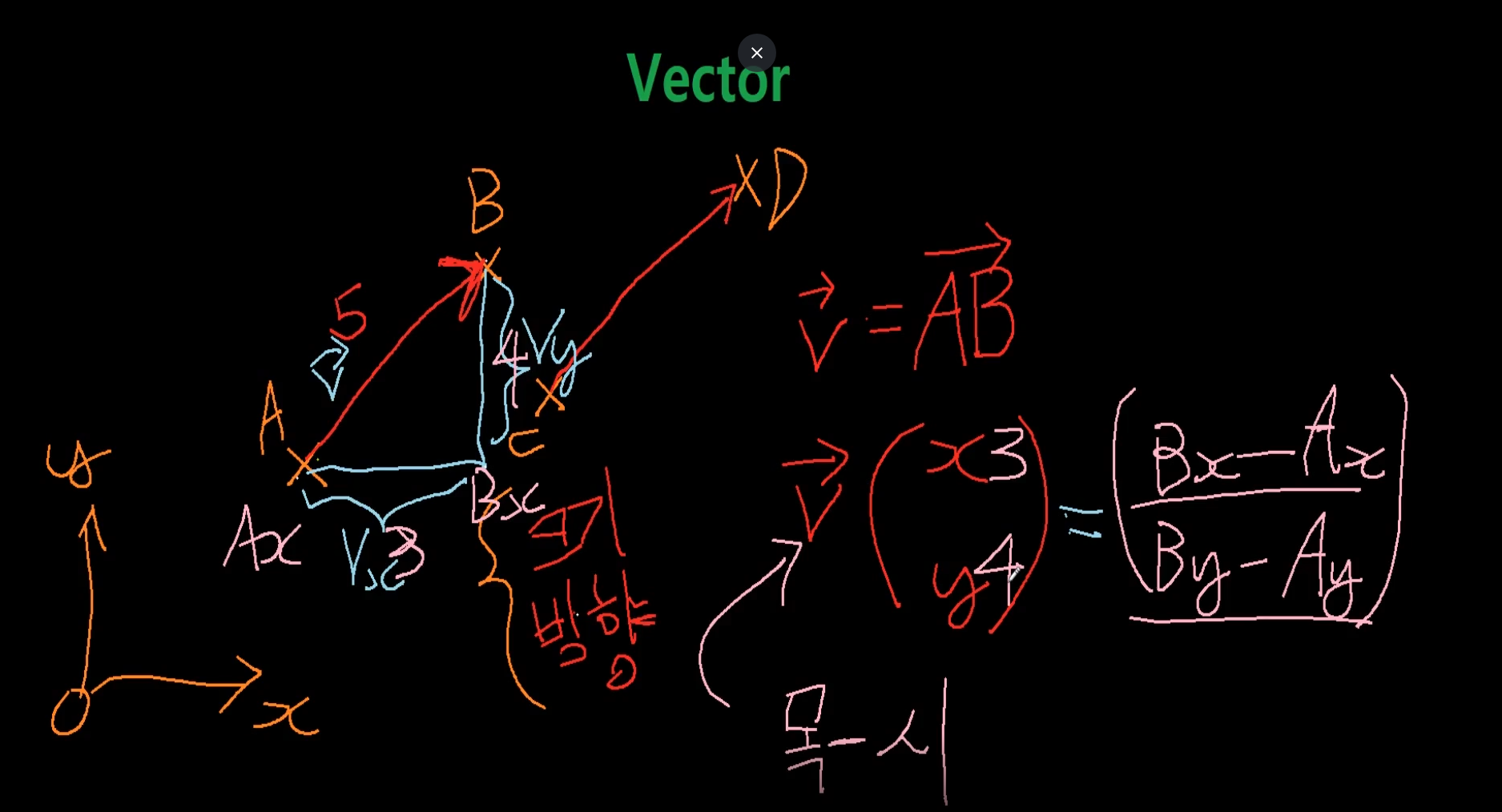
2. Vector기본 성질

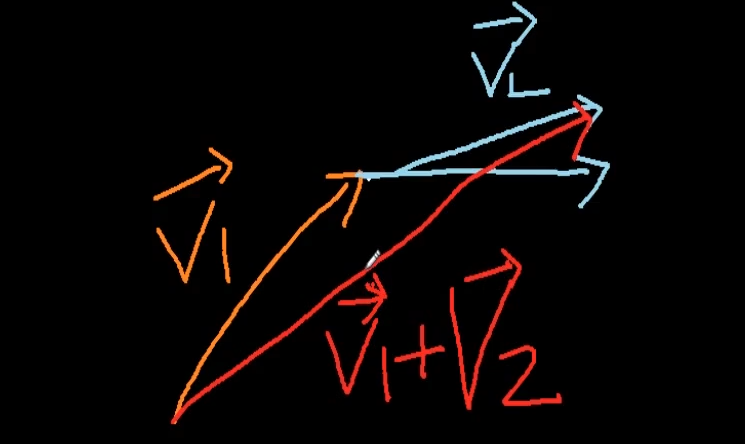
이게 벡터 덧셈임.

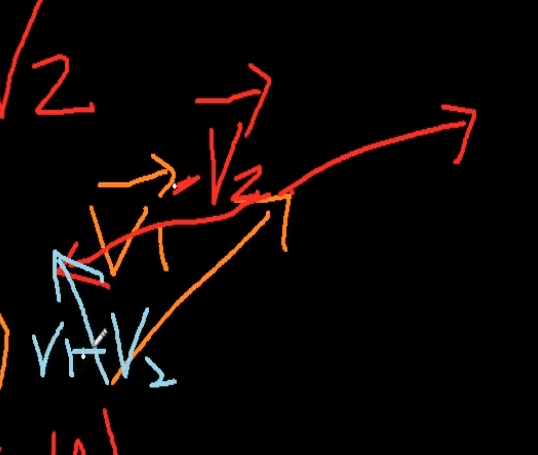
이게 벡터 뺄셈임.

벡터 사이의 곱셈, 나눗셈은 존재하지 않는다.

스칼라(고정된 값)이랑은 곱셈, 나눗셈 가능하다.

• 또한 결합, 교환 법칙 성립한다.

  

3. Vector의 크기, 단위 벡터

벡터 크기 ❗

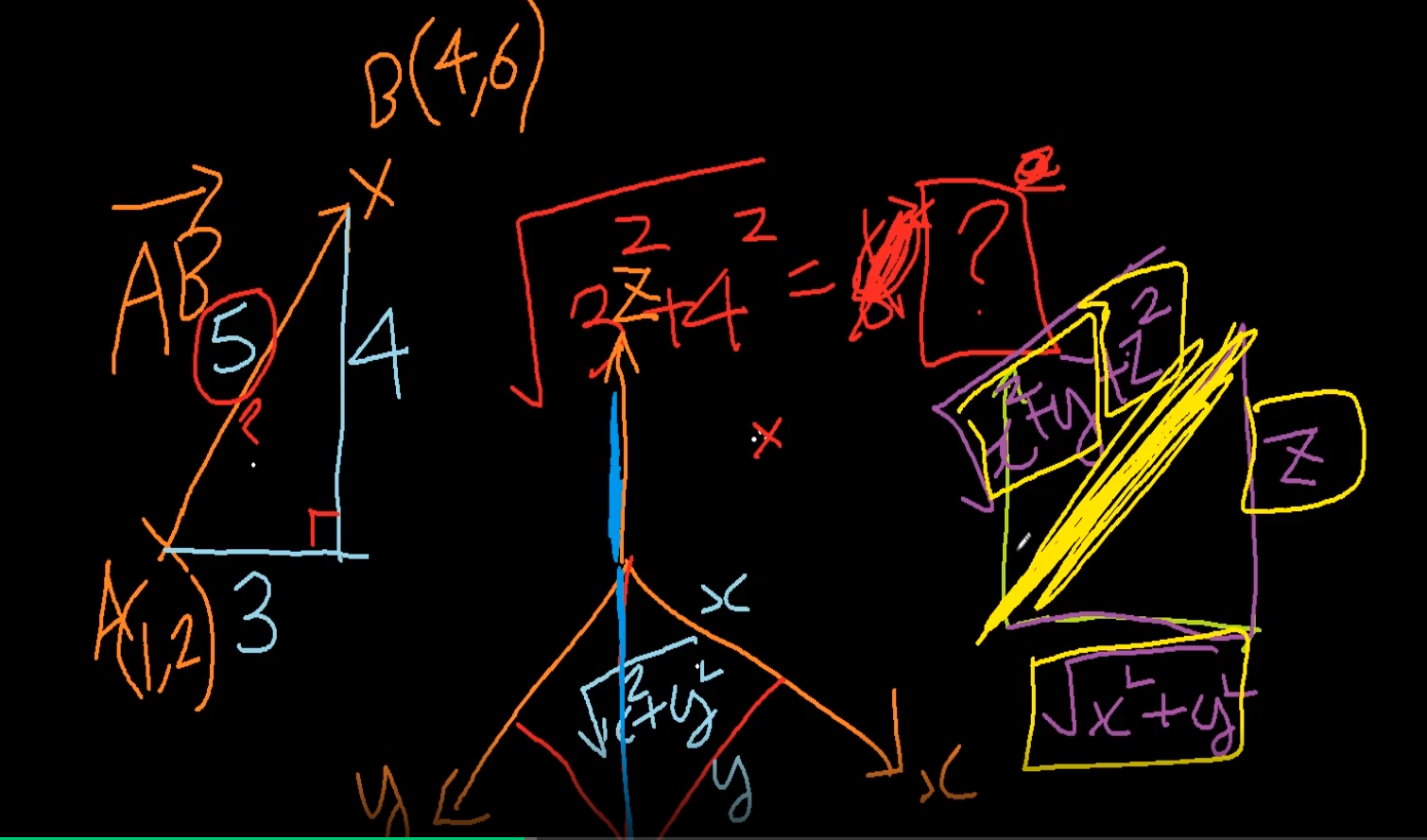
3차원은 피타고라스 법칙을 2번 사용한것이라고 생각하면 될듯.

크기는 피타고리스로 구한다.

단위 벡터 ❗

방향은 있는데 크기가 1인 벡터로 만드는게 단위 벡터임.

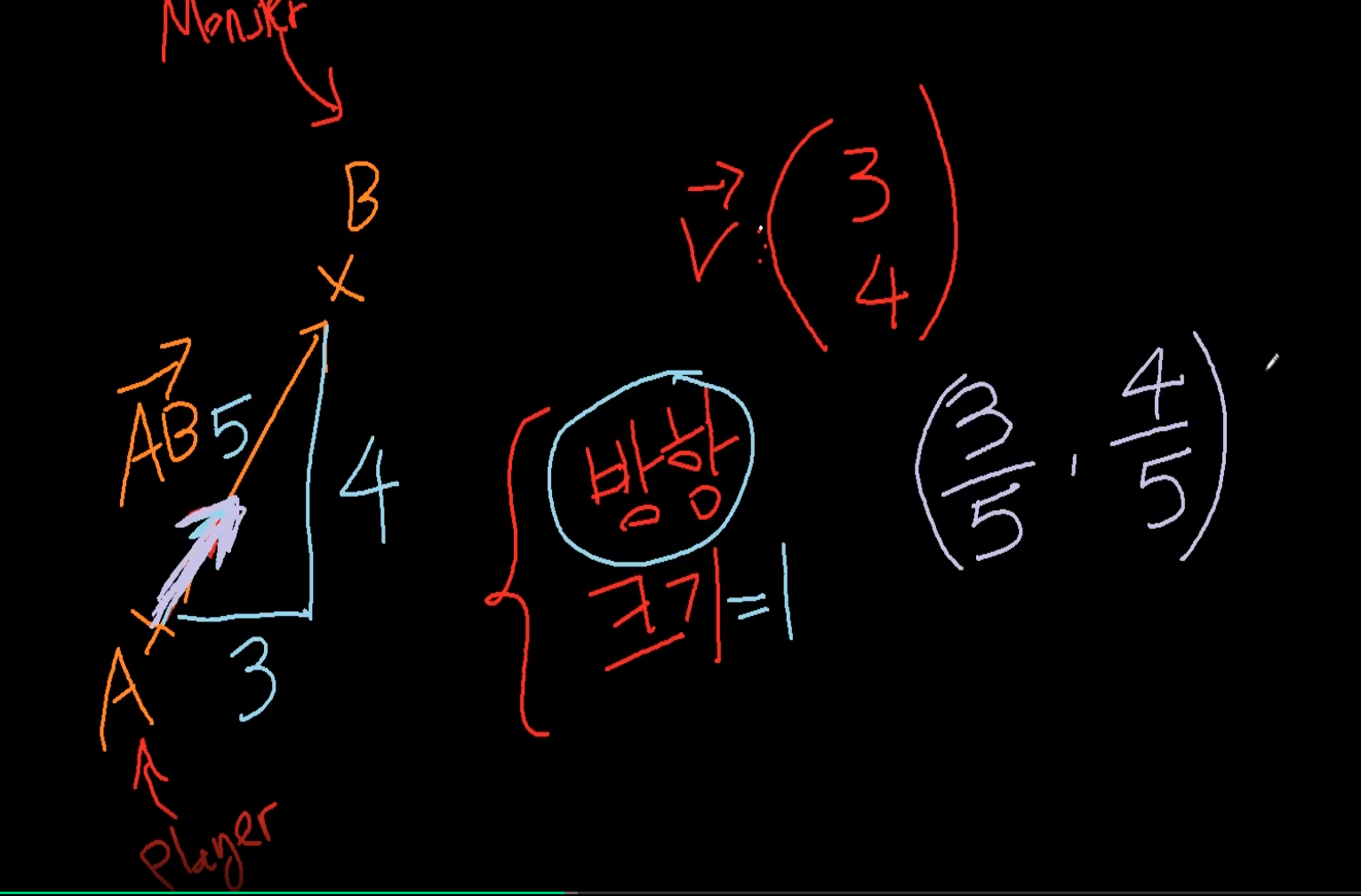
이게 단위벡터임, 각 좌표를 벡터의 크기로 나눔.

Normalized = 단위벡터로 만듦.

Magnitude = 벡터 크기

유니티나 언리얼 다 있음.

4. vector 내적, 외적

내적

내적의 값은 항상 스칼라 값이 나온다.

벡터a의 크기 벡터b의 크기 cos세타

이거 왜 사용하나? 각도와 연관성이 많은데 나중에 shader에 직교투영할 때 사용한다.

빛이 닿았을 때 그림자를 계산을 할 때 필요함.

빛이 수직으로 올 경우 cos을 계산을 하면 느린데,

a, b 내적을 하면은

---

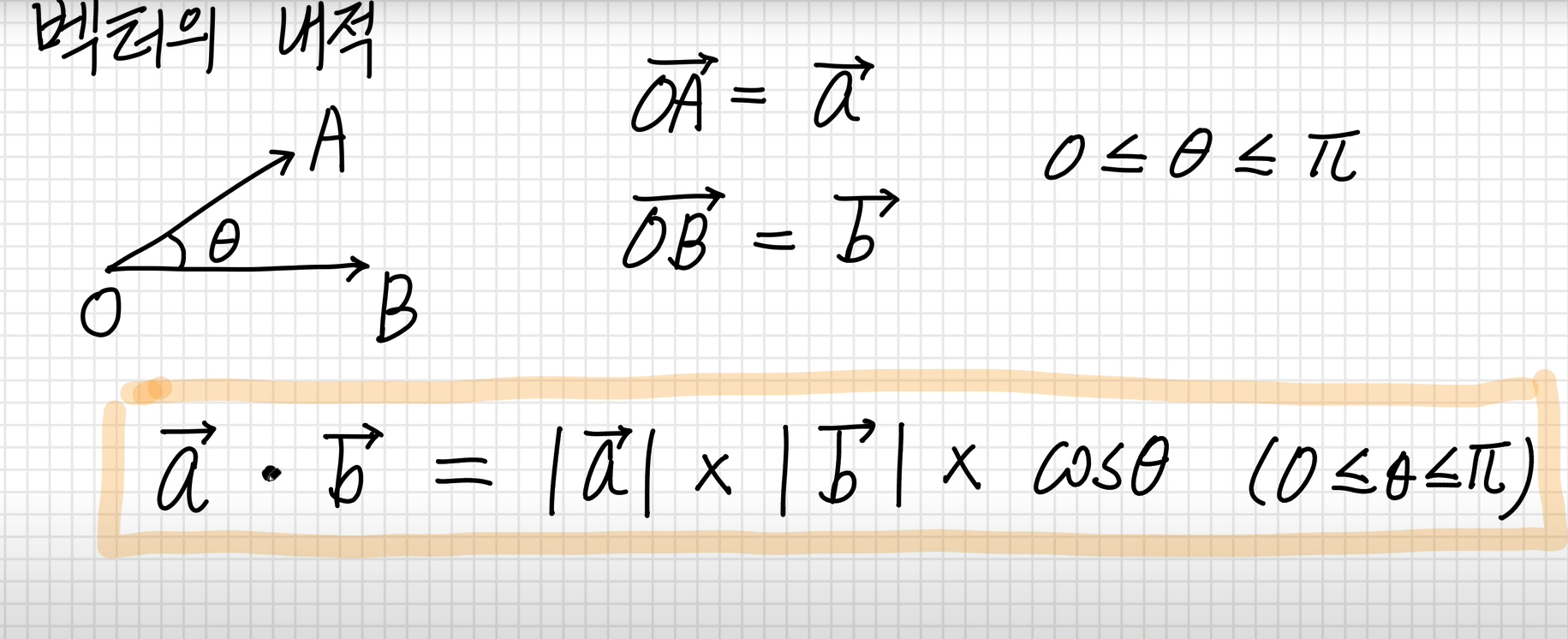
이게 벡터 내적임.

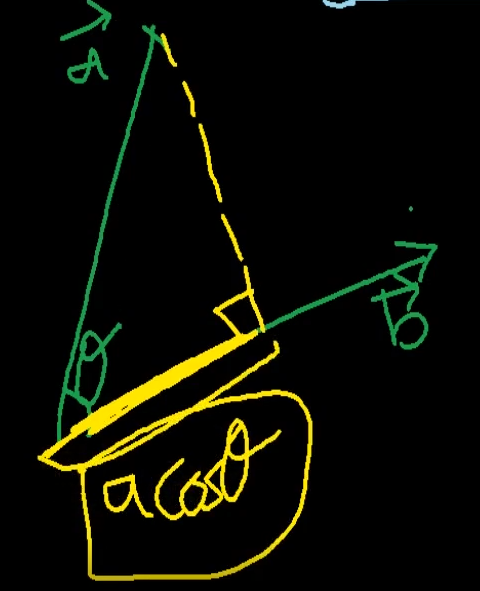
벡터의 기하학적 의미

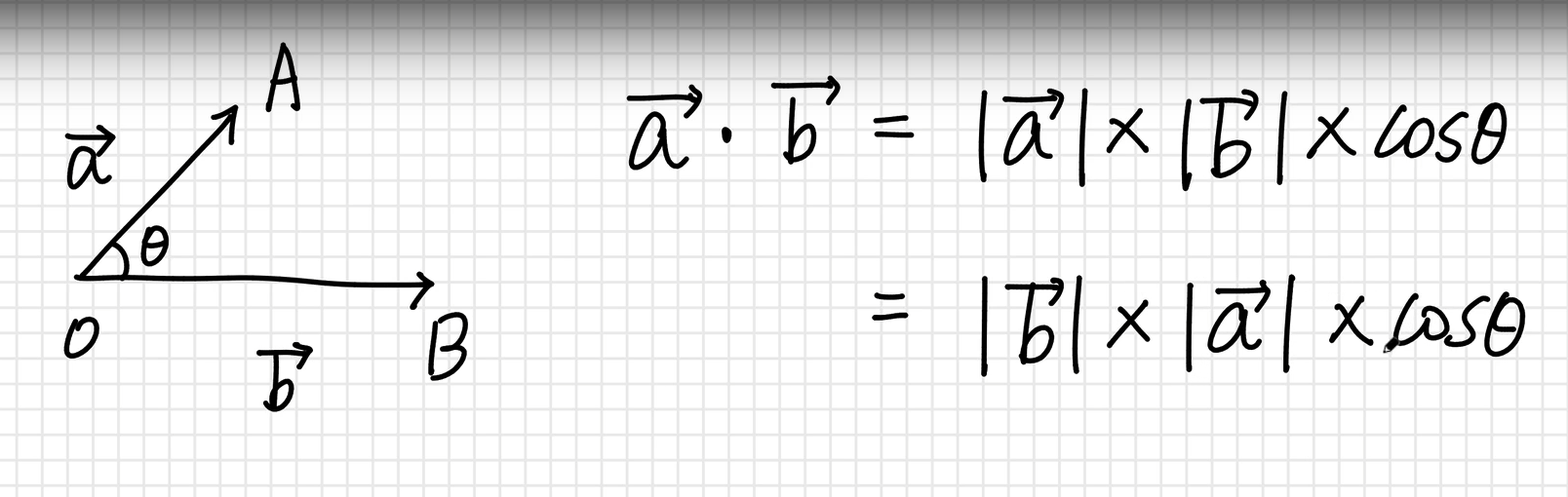
지금 vector a = 빗변 * cos세타가 OH의 길이임. => 삼각함수의 공식에 의해서

이부분이 OH의 길이임. => 단위원을 생각해보셈요.

빛 수직일 때 OA벡터의 그림자에 해당하는게 OH의 길이이다.

=> 한 벡터를 다른 벡터위에 정사영시킨 길이와 다른 벡터의 길이의 곱이다 == 내적.

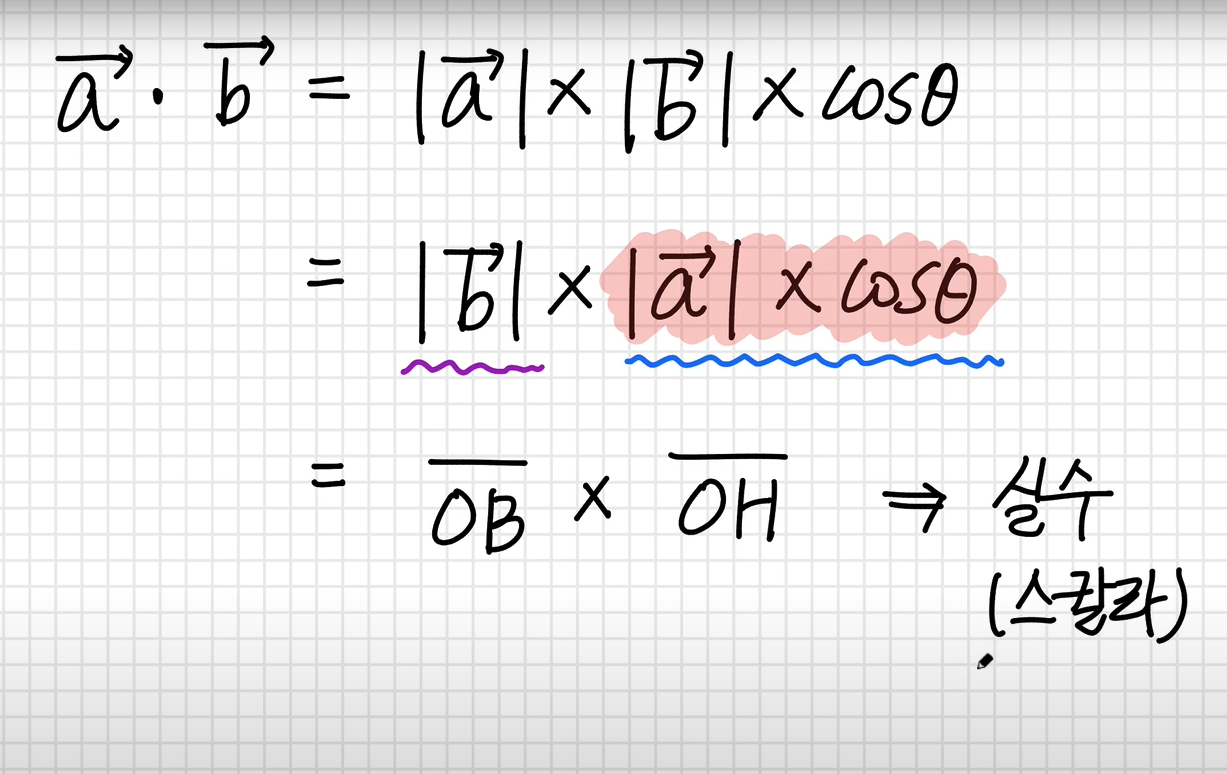
그러면 스칼라값 (고정된 값, 실수)가 나온다.

외적

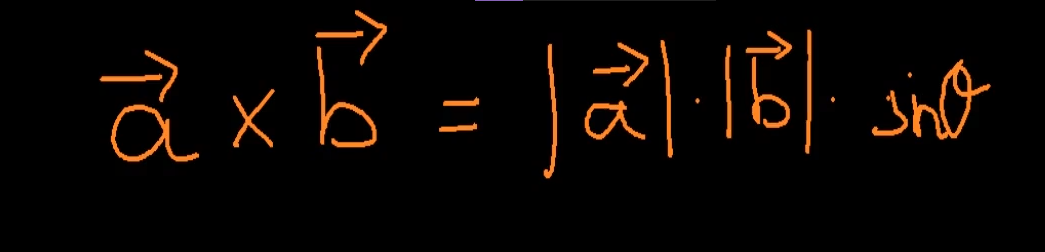
외적은 3차원 가야 좀 의미가 있음.

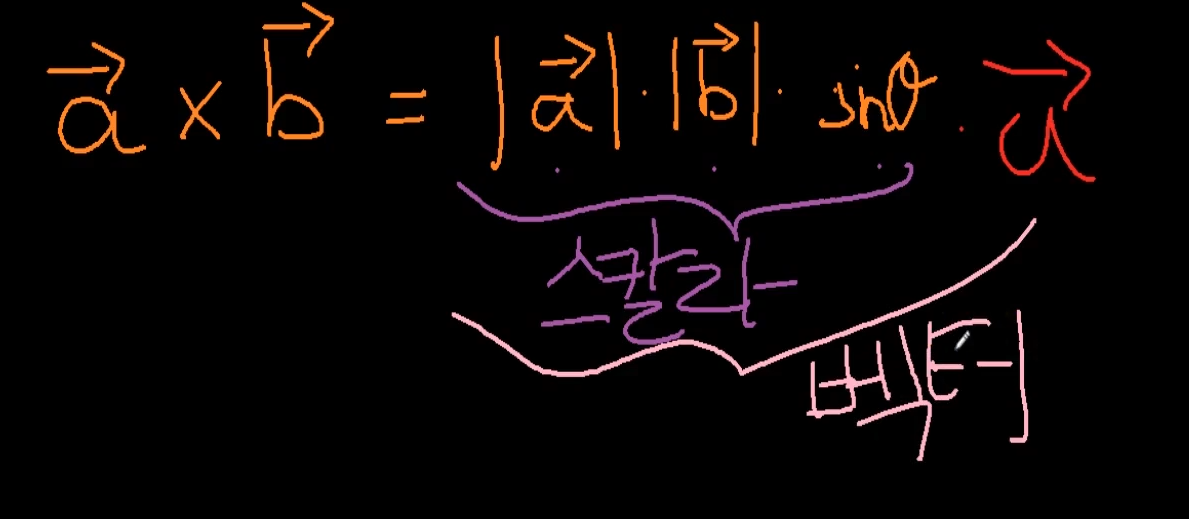
외적 결과 값은 벡터이다.

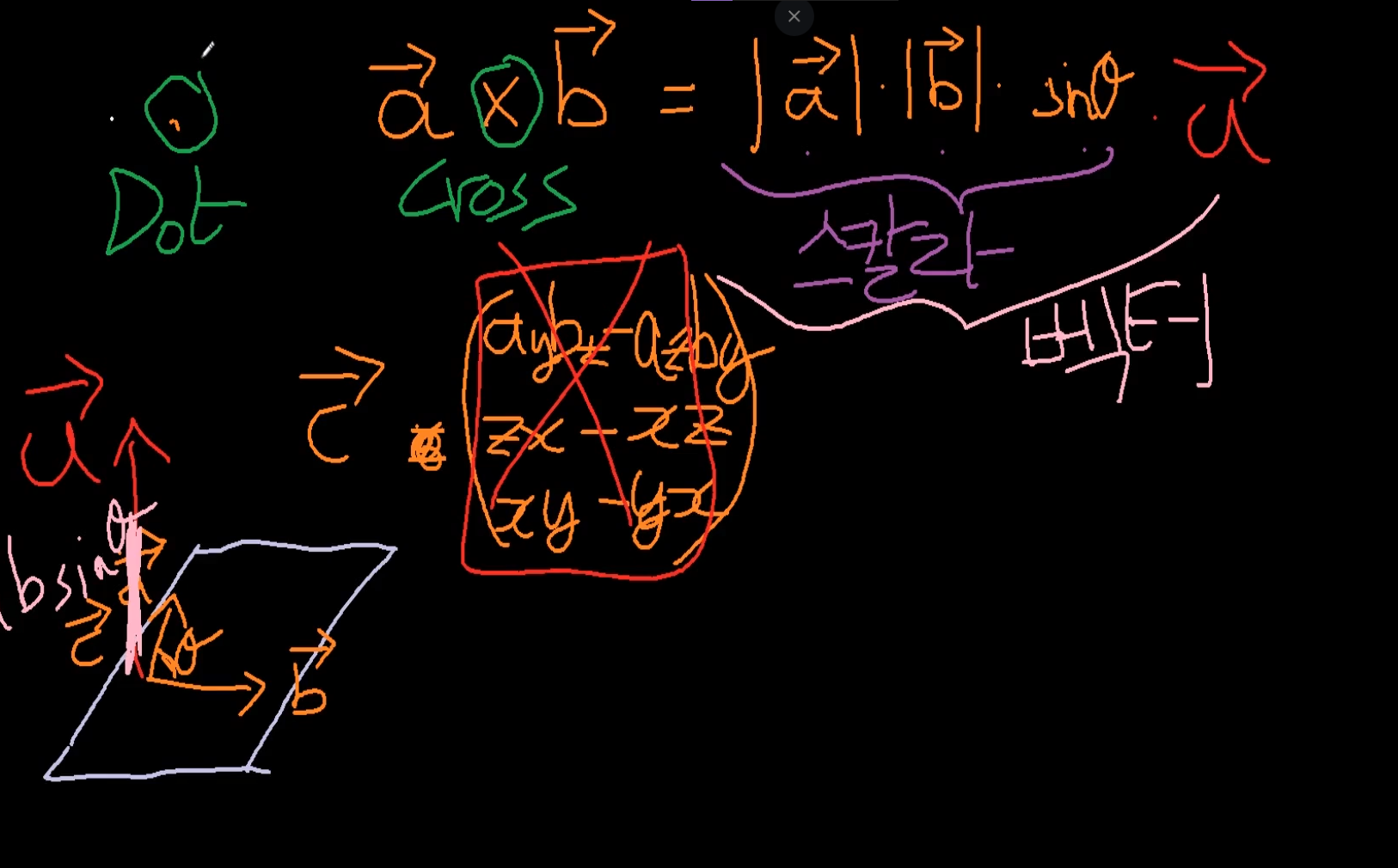
dot = 내적

cross = 외적 이라고 함수 제공을 함.

외적 왜 구하냐?

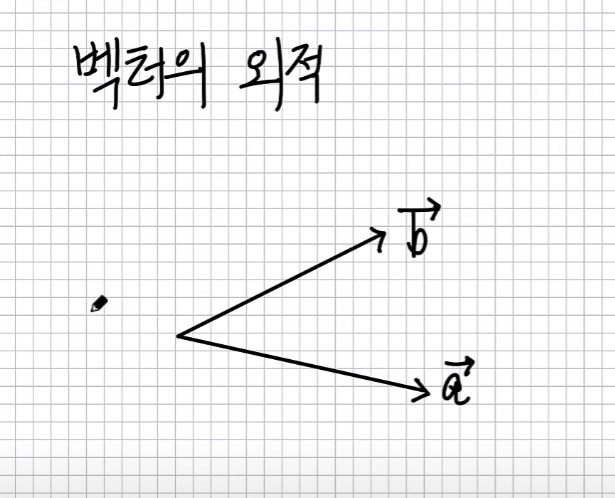
이 두 벡터의 동시에 수직인 벡터를 구하고싶을 경우

외적 어떻게 구하나?

이렇게 구함.
외적의 결과는 벡터이고 내적의 결과는 스칼라이다.

외적하면 벡터가 나옴.

외적은 내적과 다르게 교환법칙이 성립하지 않는다.

이거 안된다는거임

법선을 구할 때 유용하게 활용이된다.

5. 스킬 쿨타임 같은 부분

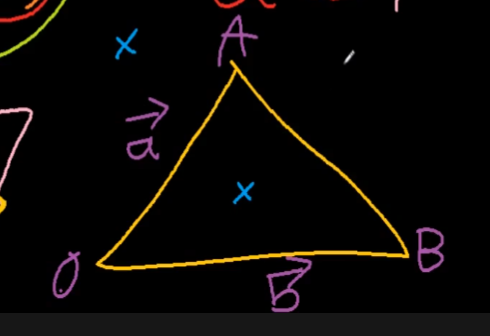
x라는 좌표가 삼각형 안에 있는지 없는지 판별할 때 외적이랑 법선벡터 자주쓴다.

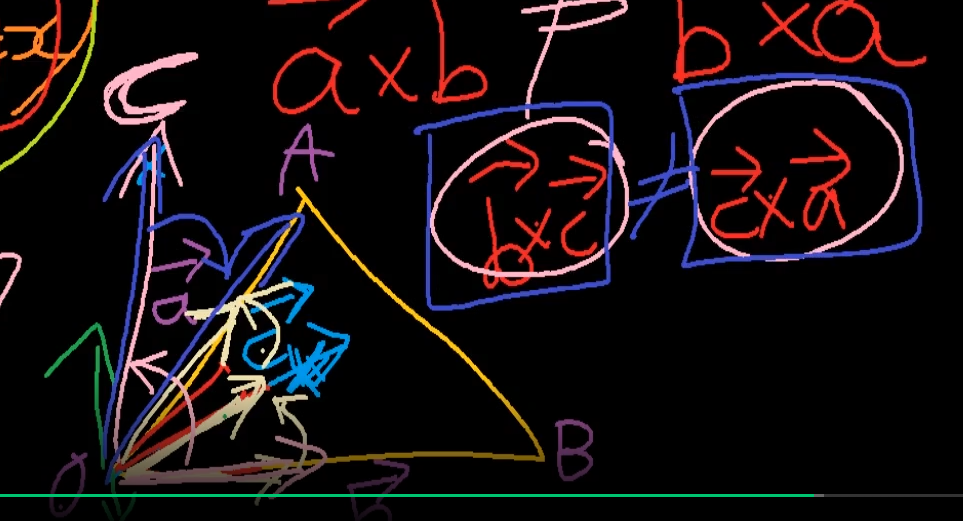
c라는 벡터를 놔두고 b c, c a 외적을 구하고 정규화를 하면은 삼각형 좌표안에 있는지 없는지 알 수 있다.

b c, c a 의 정규화 벡터의 방향이 같으면 삼각형 안에 좌표가있고 b c, c a의 외적 정규화 -> 벡터의 방향으 다르면 삼각형안에 없음.

스킬 쿨타임 UI를 영역을 외적을 이용해서 구할 수도 있다.

6. Vector활용

유니티에서만 봐도 new Vector3(); 어쩌구 사용하는데

벡터는 기하 벡터랑, 위치 벡터 이렇게 두가지 의미로 쓴다.

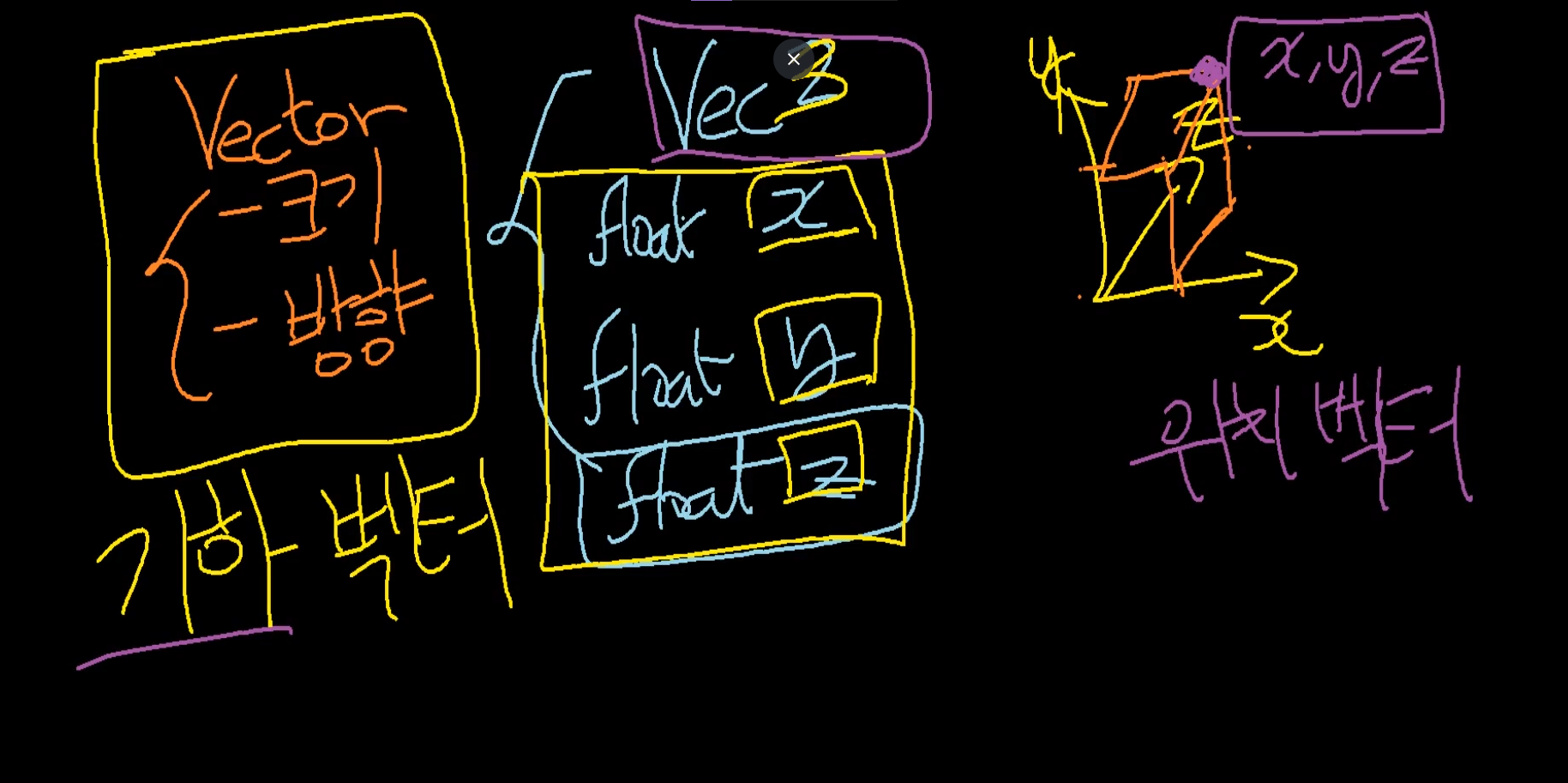
Matrix

우리가 할려는 것은 3d물체를 카메라의 각도에 따라가지고 적절하게 2d화면에까지 보이게하는 작업을 GPU한테 외주를 맡기는 것임.

1. 행렬이란

이차원 배열을 생각 => 안에는 스칼라 값이 들어가있는 상태라고 생각 ㄱ.

2. 행렬 곱셈

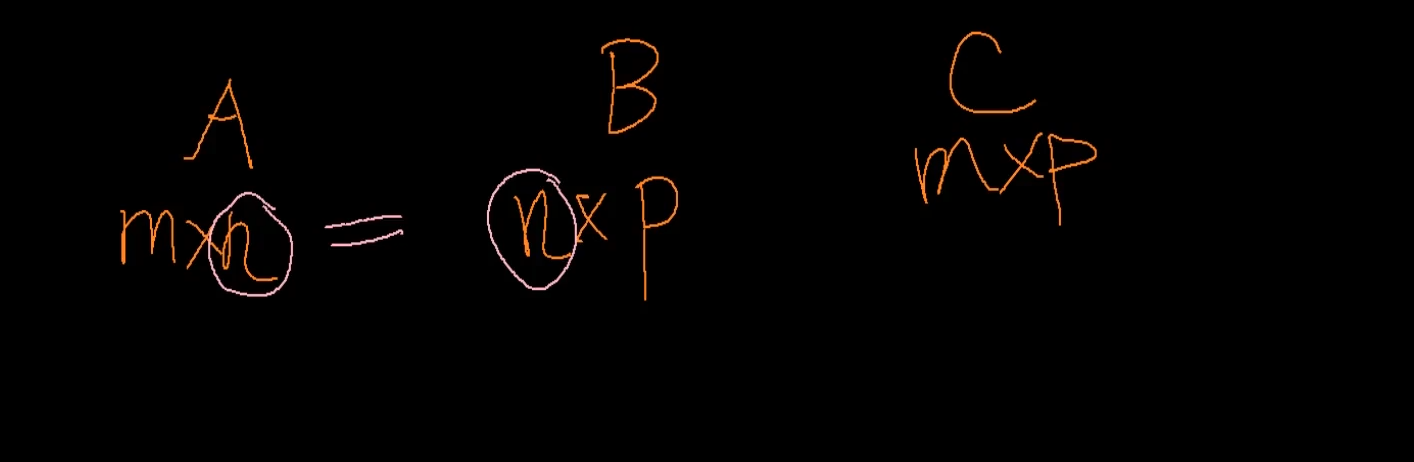
각행과 각열의 원소들을 다 곱한게 C11임.

=>

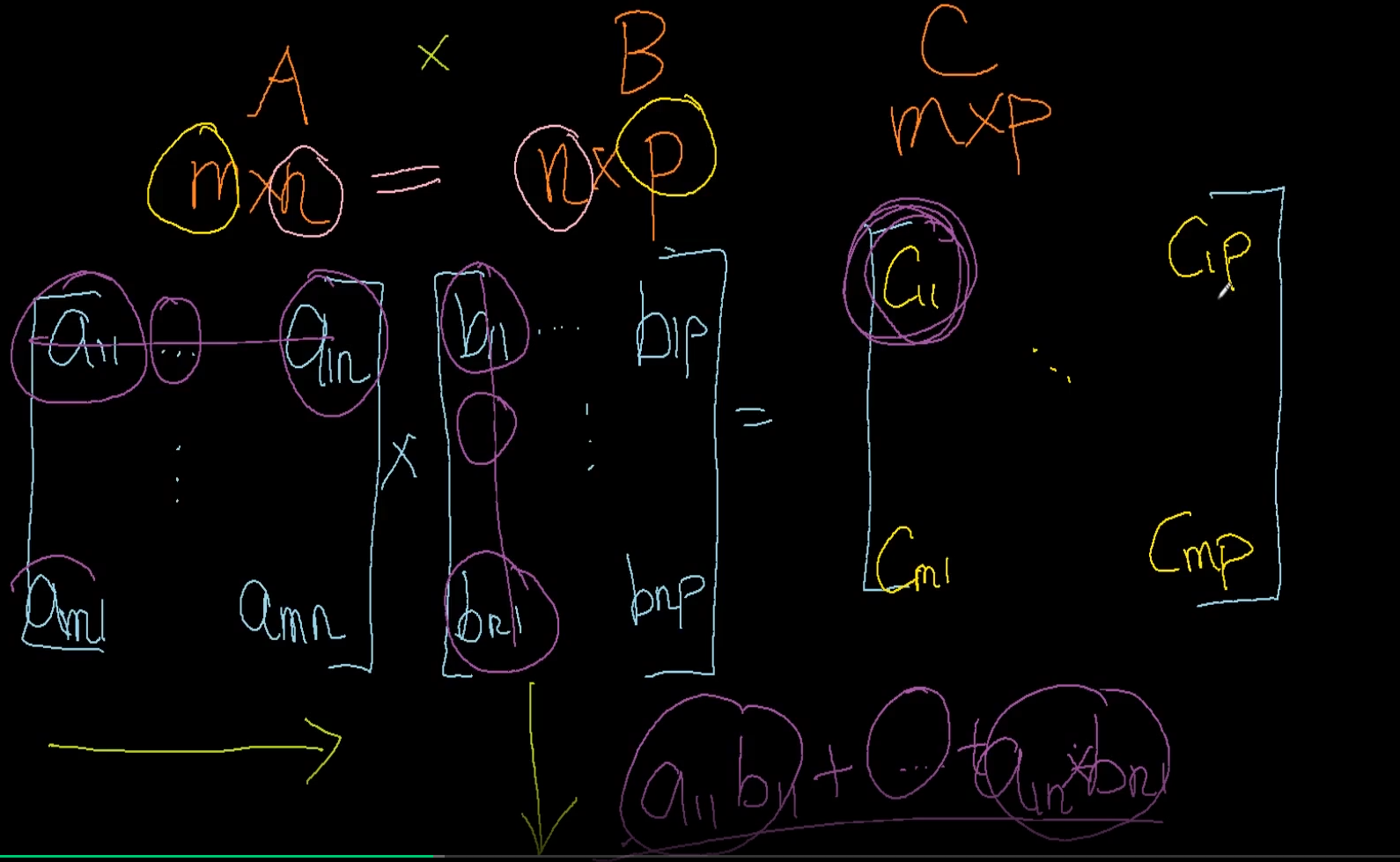
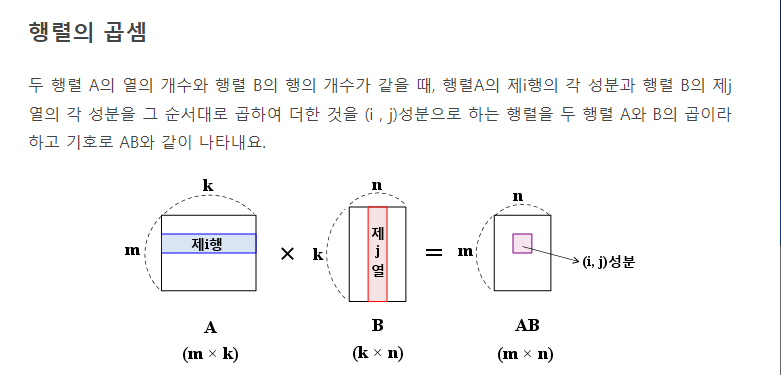
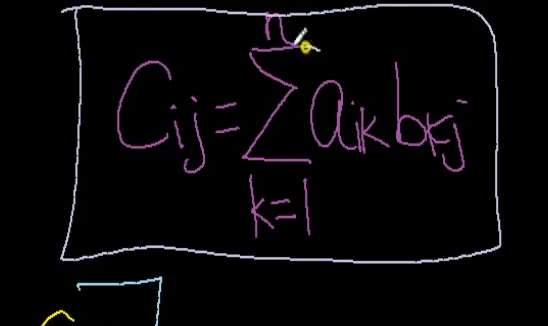
수식으로 표현하면 이럼.

이런거임.

이것을 다르게 보면은 벡터의 내적으로도 볼 수 가 있다.

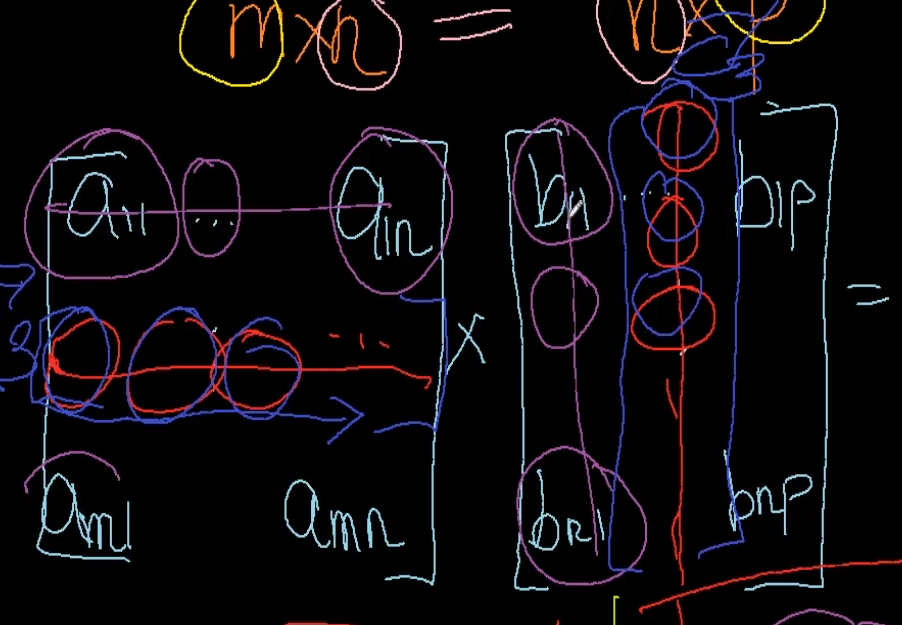
A행렬의 3행을 벡터로 보고 B행렬의 3열을 벡터로 봐서

두벡터의 내적을 구하는 식으로도 C33구하는거 씹가능.

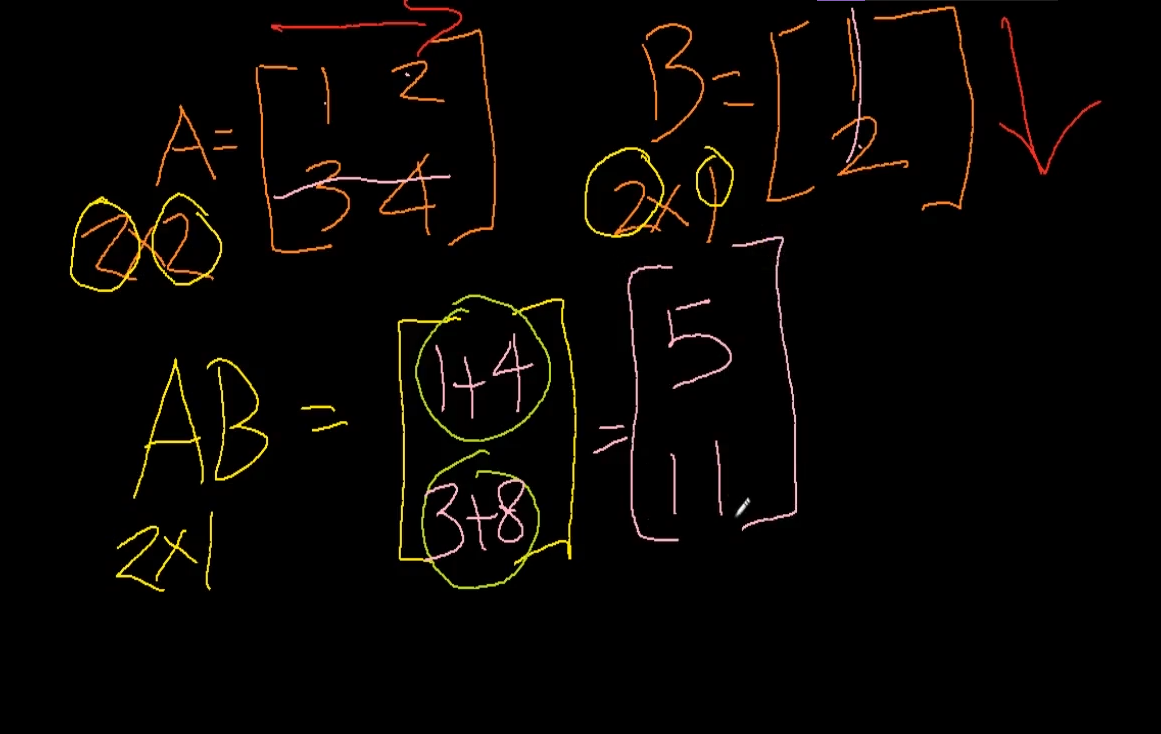
3. 법칙

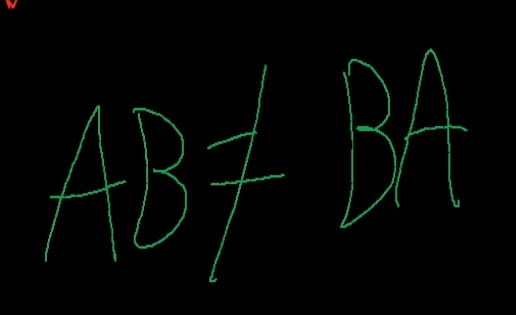
행렬 => 교환법칙 성립 안한다.

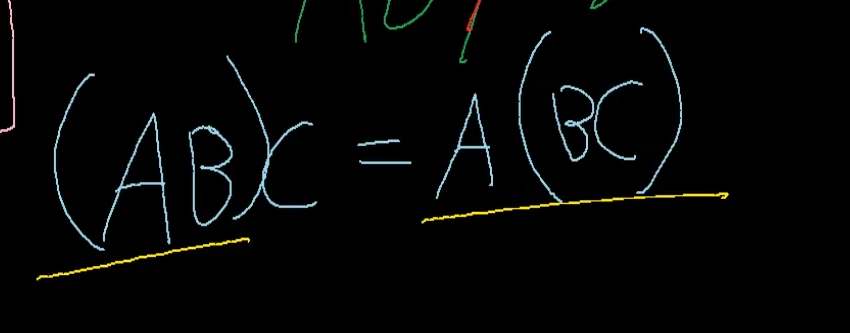
결합법칙 성립한다.

4. 특성

대각요소 제외하고 나머지 값다 0으로 채워진것들을 => "대각 행렬"이라고함.

이거는 "단위 행렬" Identity"라고함. => I

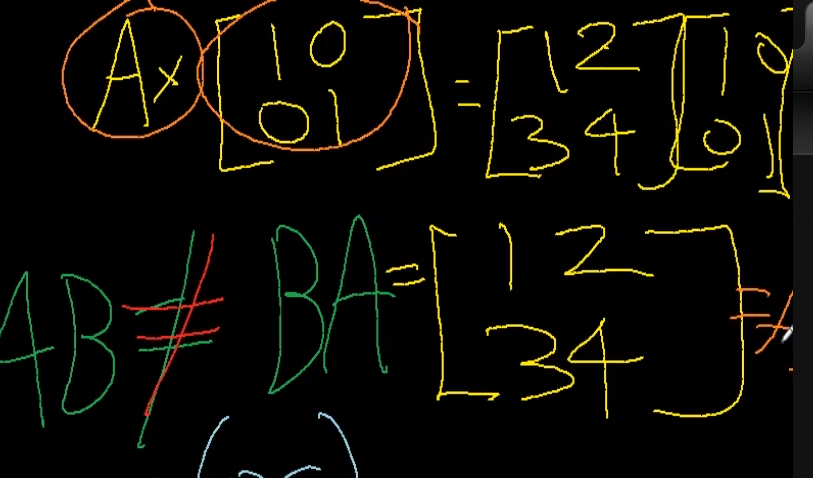
자기 자신이 나옴 => 그래서 아이덴티티

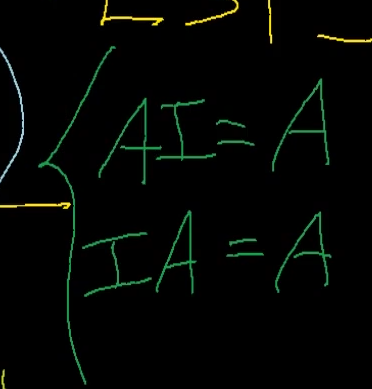
다양한 용도로 활용이 될 것이다.

5. 겜프에서 행렬

4 X 4를 쓴다.

애당초 행렬을 사용하는 이유가 어떤 벡터랑 행렬이랑 곱을 해가지고 벡터(위치)자체를 변환시키려는 것을 할려고 하는게 최종 목적임.

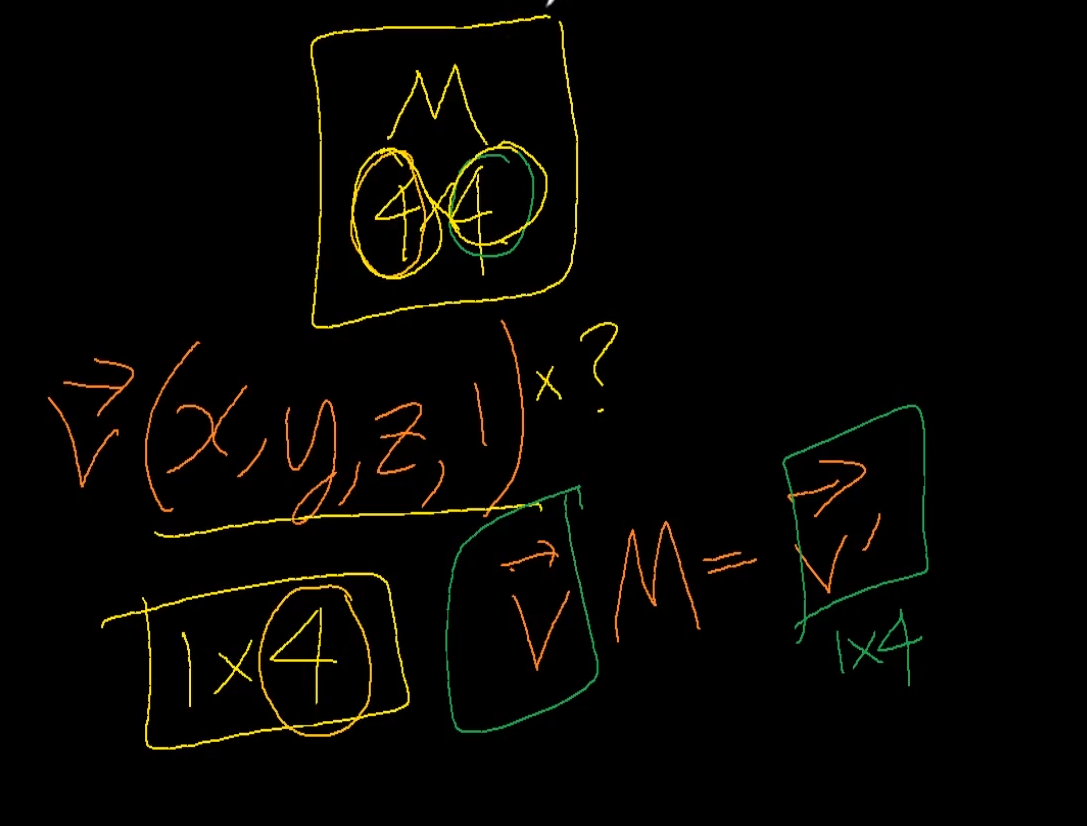
단위 행렬 중요한 이유

이럴경우 역행렬 관계임.

역행렬은 100%확률로 존재하는것은 아님.

역행렬이 존재한다면은 가역행렬임.

6. 역행렬

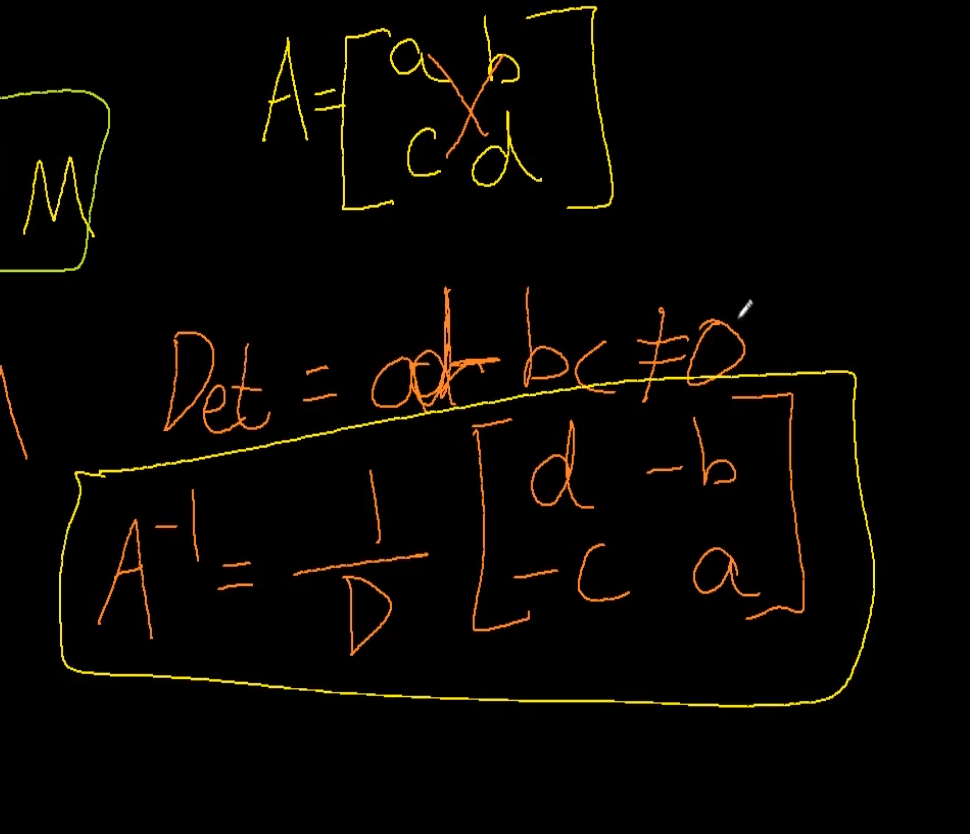
2차원 행렬의 역행렬 공식임 => 학교에서 했던거 조금 기억난다.

ad - bc != 0 이라면은 역행렬이 존재한다.

7. 게임에서 역행렬 => 전치 행렬

ㅈㄴ 쉽게 구할 수 있음.

전치 행렬 = 행과 열을 뒤짚은거

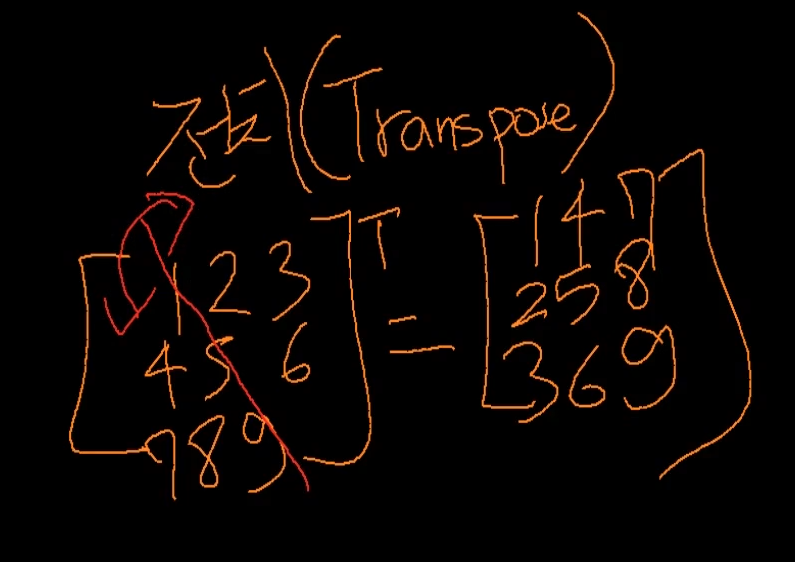
전치 특징

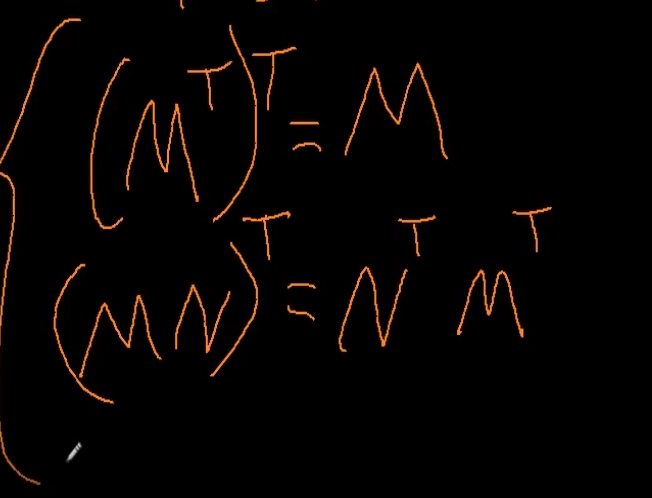
선형대수에서 함.

8. 직교행렬 ❗

M이라는 행렬이 있을때 각 행을 벡터로 보고 v1 ∘ v2 => 0 다 0이 나오는데

벡터의 내적값이 0이라면은 직교함. 이게 직교행렬임.

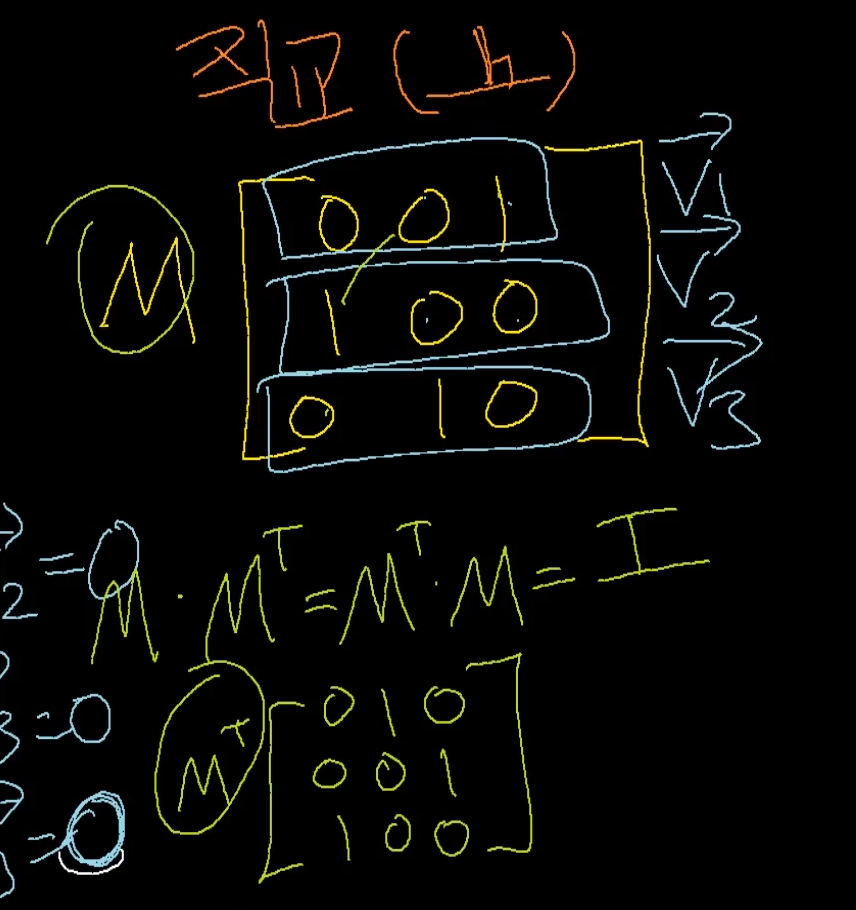
이렇게 전치 행렬나오는데

직교행렬 -> 전치 행렬구해서 곱하면 Identity나옴.

즉,

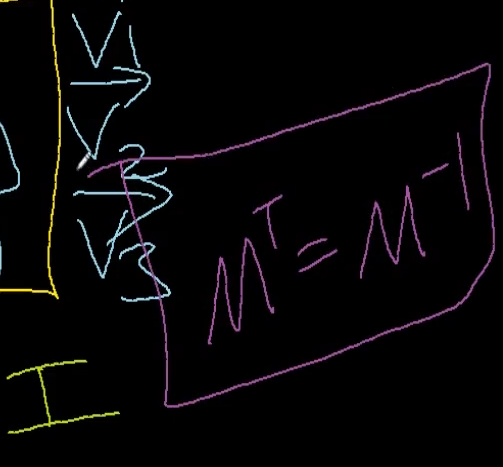
M이라는 직교행렬의 전치행렬은 M이라는 행렬의 역행렬이다.

Scale, Rotation, Translation

행렬이 게임에서 어떻게 적용되는지 보도록 하자.

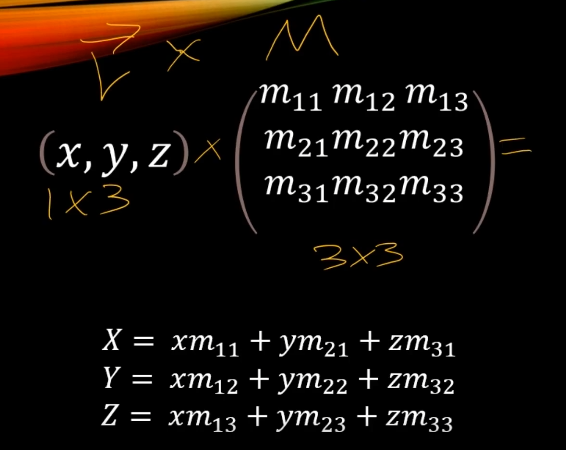
이런 행렬 연산을 하면은 1x3행렬 나옴.

벡터랑 행렬이랑 연산.

벡터를 변화 시킬때 기억해야할 3총사 있음

=>

Scale, Rotation, Translation

3D상의 물체를 2D화면으로 투영하는 전과정을

수학적으로 연산을 할 것이다.

거기서 변환행렬씀.

그 중에서도 Translation중요함...

Translation할 때 3차원 행렬로는 계산을 할 수 없다.

그래서 "동차 좌표계"를 사용을 한다.

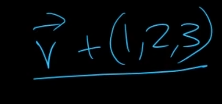
이게 불가능 하기 때문에.

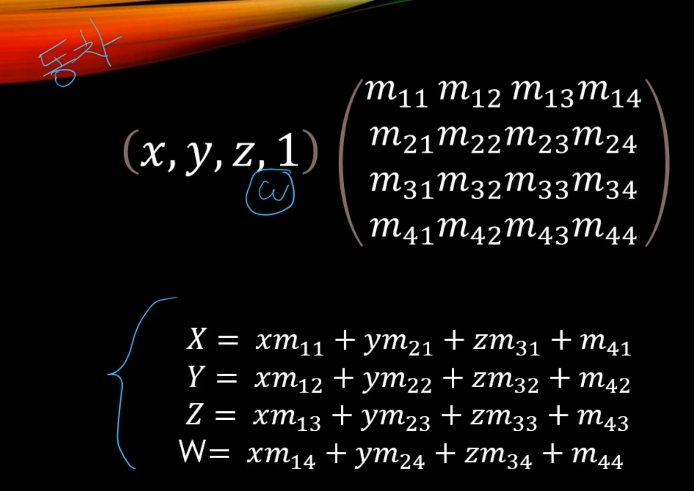
w는 의미를 갖기보다는 연산을 도와주는 도구느낌임.

1. T

v라는 벡터에 (1, 2, 3)만큼 이동을 시키고 싶을 경우

동차 좌표계를 사용을 한다.

m41, m42, m43에 값이 들어가고

w = xm14 + ym24 + zm34 + m44가 1이 되어야 하기 때문에

m14 = 0, m24 = 0, m34 = 0, m44 = 1이 되면된다.

결국 이동과 관련된 녀석은 m41, m42, m43이다.

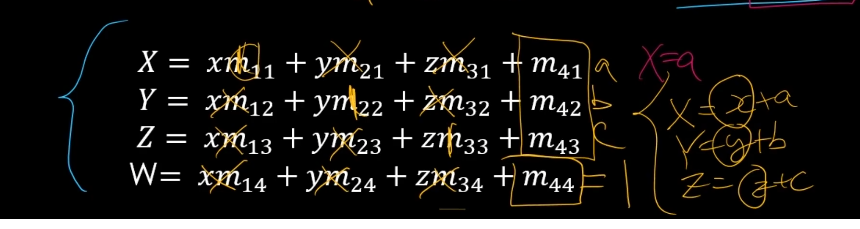
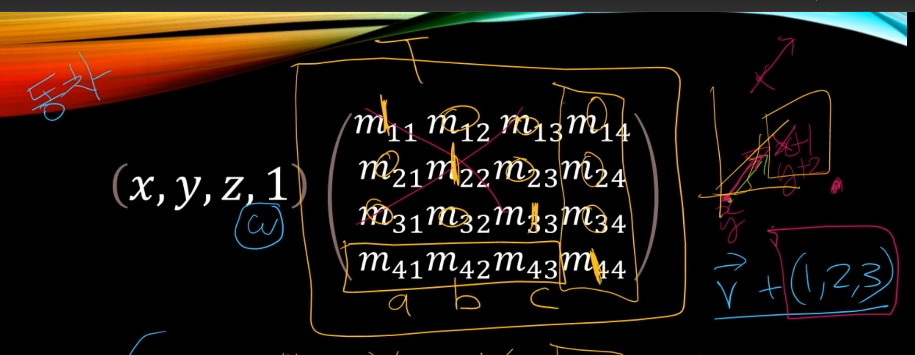
이게 우리가 원하는 T이다.

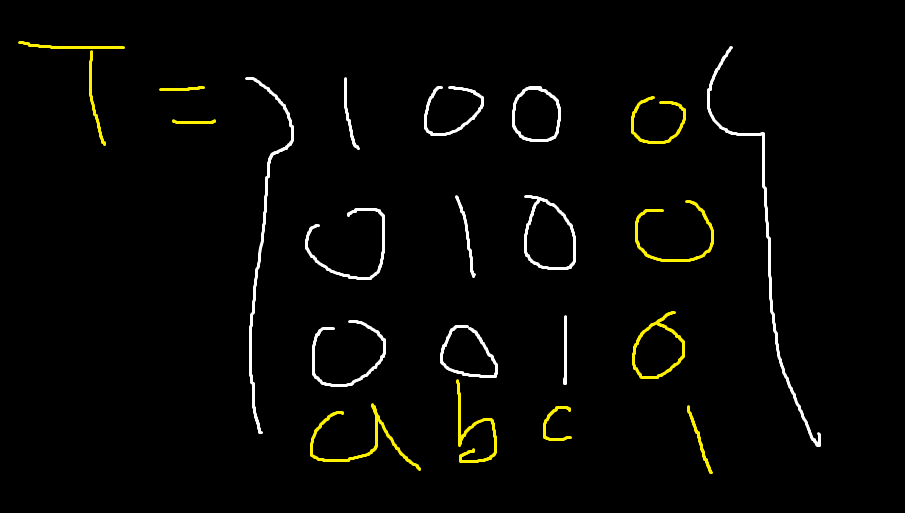
2. Scale

x좌표로는 a만큼, y는 b만큼, z는 c만큼 늘어나길원하는 것임.

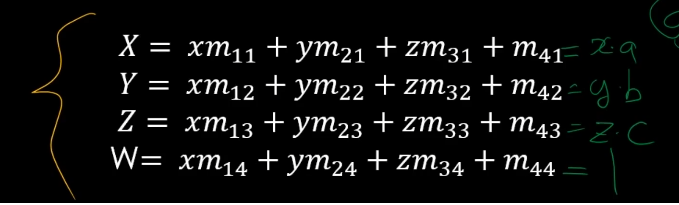
X = xm11 + ym21 + zm31 + m41 = x * a

이것을 만족을 해야함.

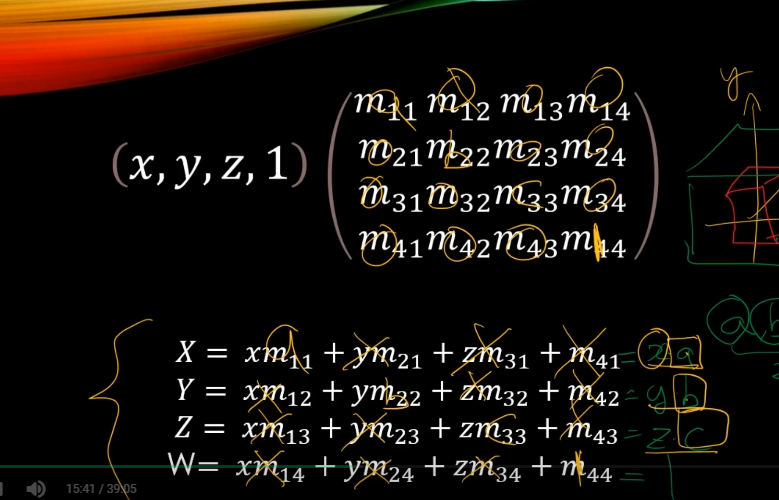
그래서 대각 성분이 a, b, c가 되어야한다.

조심해야할 부분.

지금 원점이 아니라 저기 (x, y, z)에 물체가 있고

행렬변환을 통해서 크기를 키우게되면은

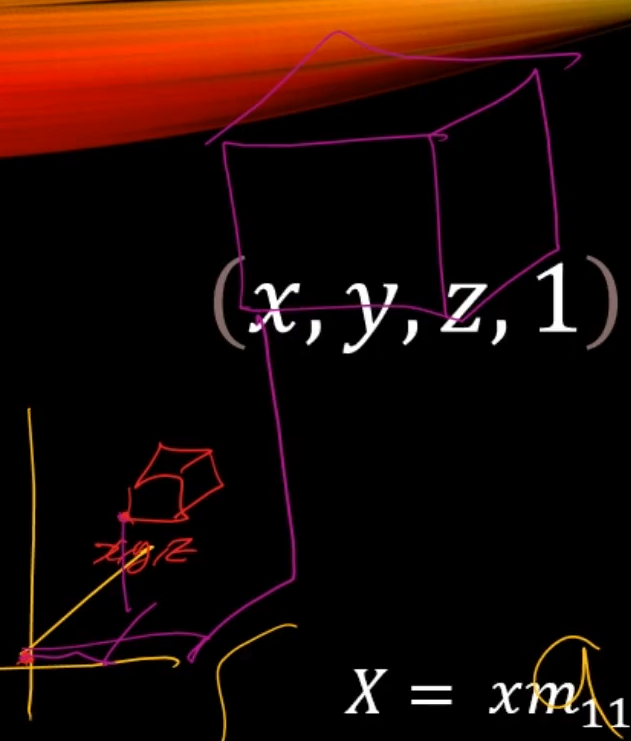
x가 a배만큼 늘어나고 y도 b배만큼 늘어나고 z도 c배 만큼 늘어난 좌표에서 물체가 커져버려서

엉뚱한 좌표에서 커질 수가 있다.

이거 이해하는게좀 중요하다.

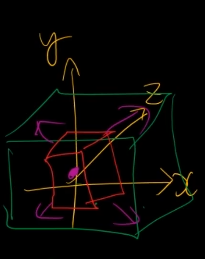
원점에 있을 경우에는 예상대로 몇배만큼 커지지만,

중점 좌표를 어디에 잡냐에 따라서 다르게 커지거나 막 그런다.

3. Rotation

T, S보다 좀 어렵다.

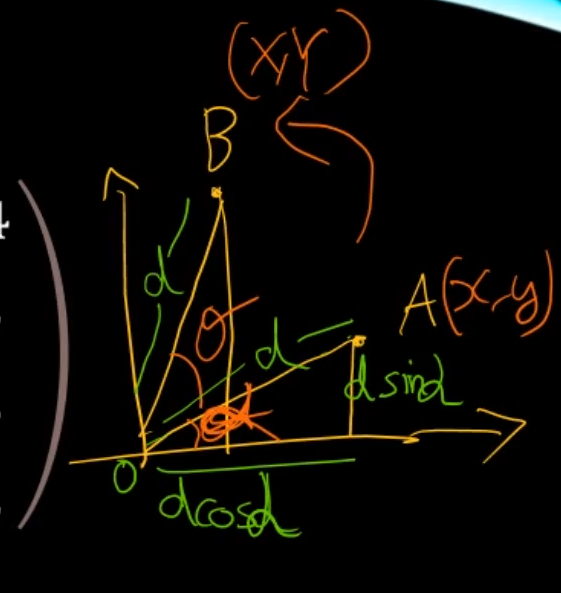
A에서 B로 회전을 시킬때

점 A에서의 삼각형의 x길이는 d * cos(α) 이고

y길이는 d * sin(α)이다.

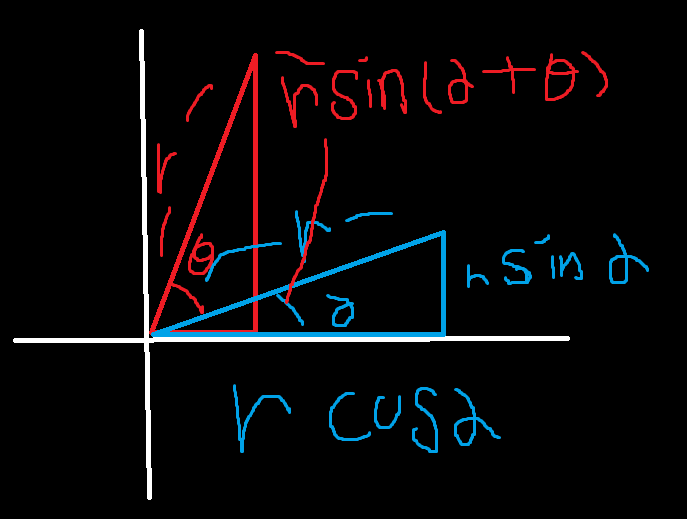
빨간 삼각형 세로 높이를 풀어 쓰면은

x는 r * cos (세타 + 알파)

y는 r * sin (세타 + 알파)

이기때문에

사코코사, 코코사사

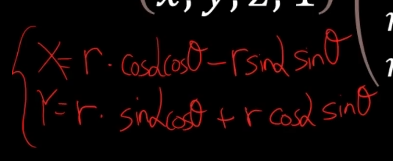
cos는 +이면 => 부호가 반대,

sin은 +이면 => 부호 그대로임.

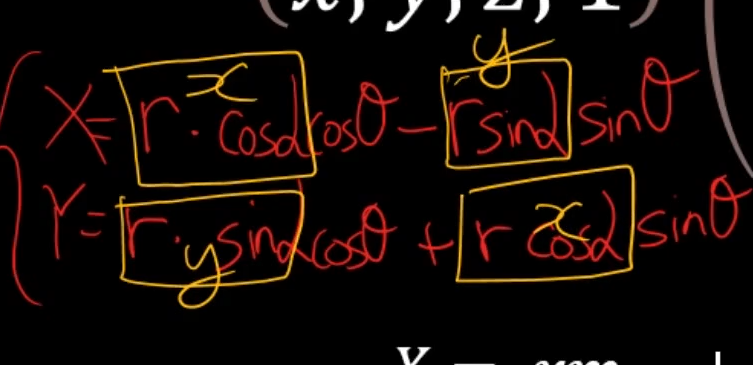
노란 박스 부분을 x, y이런식으로 치환이 가능함.

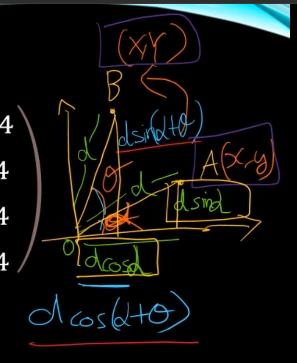
그림 보셈요.

결국

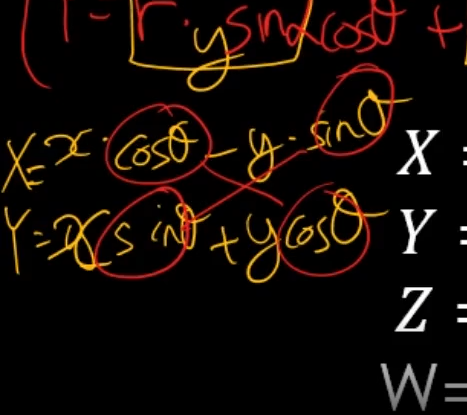
이게 결론이기는 함.

그래서 결국 z축 회전행렬 자체가

z축 "회전 행렬" 이런모양으로 만들어지는 것이다.

x, y는 x부분이 1, y부분이 1이고 나머지 부분을 계산을 하면 되는것이다.

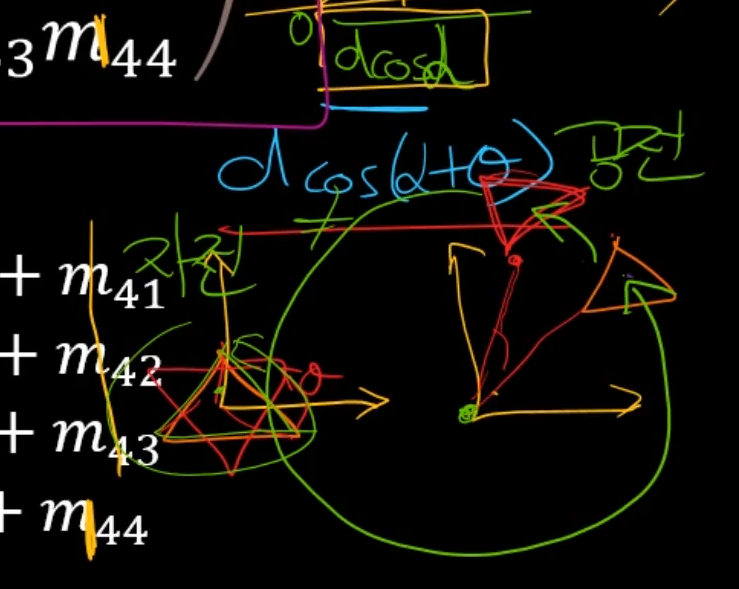
물체가 어떠한 상황이냐에따라서 자전, 공전하는데

공전하는 경우는 거의 없다.

행렬 교환/결합

행렬 연산할때 교환법칙은 말이 안되는데

결합은 말이됨.

나중에 GPU한테 데이터 넘길때는

이세가지 연산을 먼저한다음에 오브젝트의 정점을 연산이 끝난 행렬과 연산을 하도록 시킴.

SRT ❗

대신에 S, R, T순서대로 계산을 해주어야함.

만약 순서가 바뀌면 이동을 하고 원점은 저 멀리 있는 상태에서 회전을 하게되어 공전을 하는 느낌으로 됨.

좌표계 변환 행렬

물체의 좌표는 그대로있고 좌표계의 좌표가 변화해서 물체의 좌표가 변화하는 일도있다.

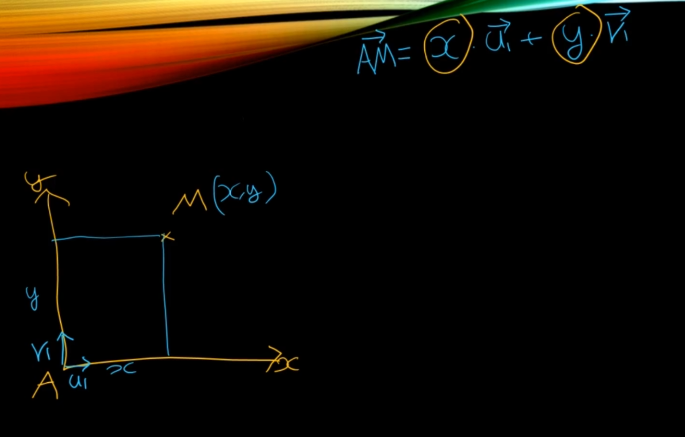
AM은 이렇게된다.

근데 어떤 이유에선가 좌표계의 기준이

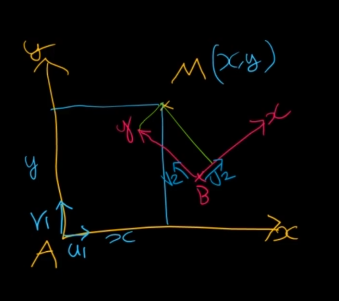
B로 바뀌면 이런식으로된다.

좌표계 변환왜 하냐하면은

게임에서 모든것은 카메라 기준이다.

그래서 카메라를 기준으로 모든 좌표가 바뀌어야하기 때문에 좌표계 변환 행렬을 사용하는 것이다.

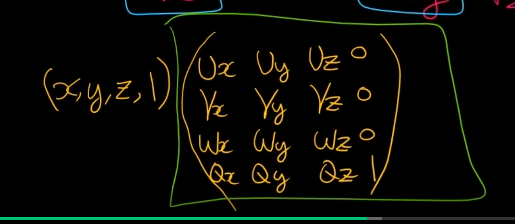
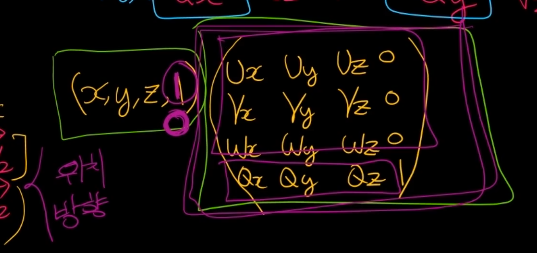
위치일 경우에는 x, y, z, 1

방향을 경우 x, y, z, 0이다.

World, View 변환 행렬

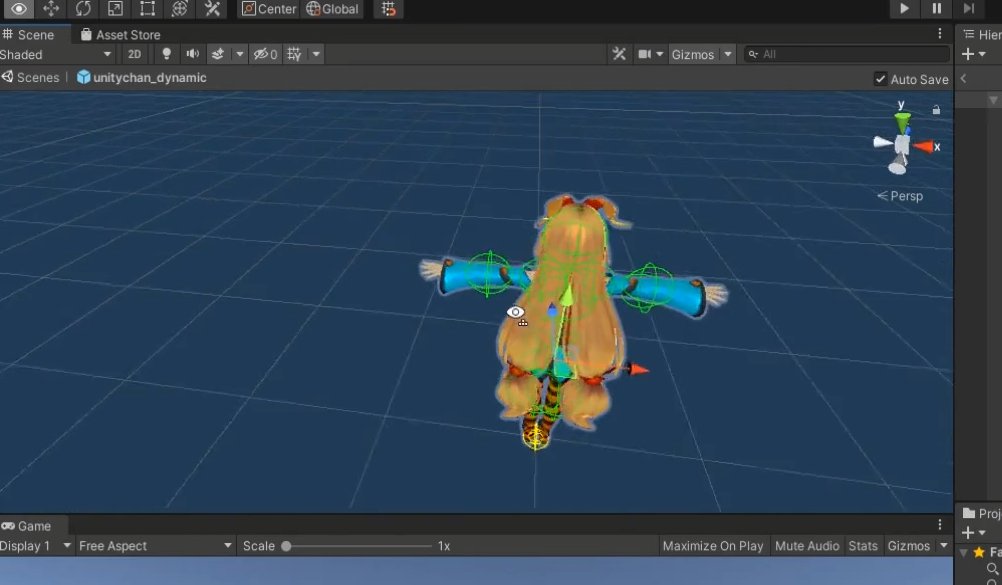
각 오브젝트들마다 Local좌표계를 가진다.

중요한것은 각 모델들 마다 "Local Space"를 가진다는게 중요하다.

Local Space에서는 상대적으로 혼자 있는 것마냥 이렇게 배치가 되는데

Game세상에서는 World Space에서는

다른 좌표에 배치가 된다.

이것도 World행렬을 계산을 해서 지금 저 모델을 배치를 한 것이다.

그런데 게임 세상에 존재하는 모든 물체들이 카메라가 있기 때문에 카메라를 통해서 보여지는데

그래서 모든 물체들을

World 좌표계에서 Camera좌표계로 바꾸어 주어야한다.

즉, 카메라의 위치를 원점으로 해가지고 카메라가 바라보는 축을 z축으로 해서 모든것을 다시 연산을 해주어야한다.

그래서 카메라가 바라보는 좌표계를

View Space || Camera Space라고도 한다.

(ISpace)

Local 좌표 -> Wolrd 좌표 -> View Space로 변환 발생해야함.

근데 이게 끝이 아니고 "투영 단계"가 발생함.

Loacl -> World -> View -> 투영

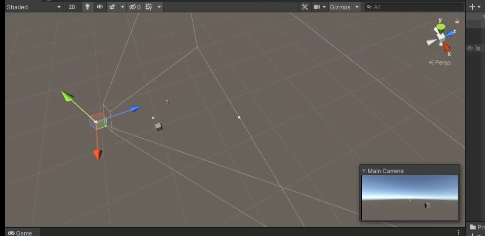
카메라의 이 범위 안에서만 물체들이 보인다.

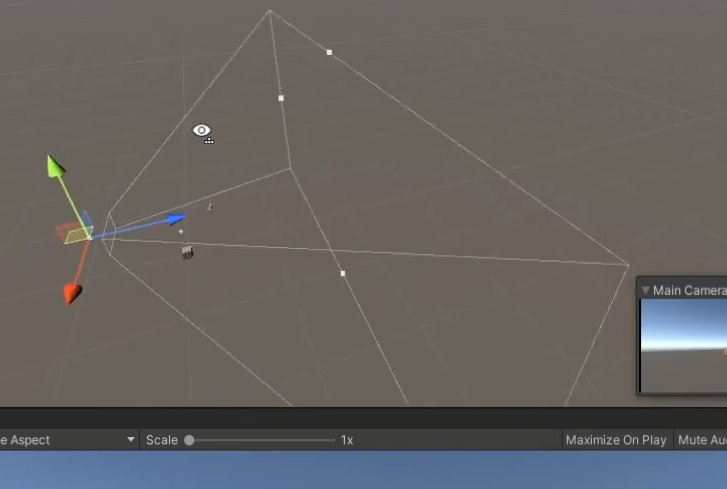
이 양식장안에 들어오는 모든 물체들을 Projection을 해주게된다.

즉,

이 near?화면에서 비율을 유지해서 밀착을 시켜주어야하는데

그 단계를 Projection == 투영한다고 하고,

물체가 범위 안에 들어가면은 Flip Space 라고한다.

지금 카메라

좌표가 이럼.

마지막은 View Port Space에 그려주는 작업이 남아있다.

여기 Game Scene말하는 거임.

그래서 "물체"는 어떻게 보여지는 것이냐면은

Local 좌표 -> World 좌표 ->
View Space -> Projection(투영 -> Flip Space) ->
View Port Space(Screen Space) -> 사람 눈

이 순서임.

---

투영 방법도 "원근 투영", "직교 투영"이 있음.

원근 투영은 말그대로 원근법 느껴지는것이고

UI같은게 원근 적용안 받게 직교 투영함.

---

1. 순서

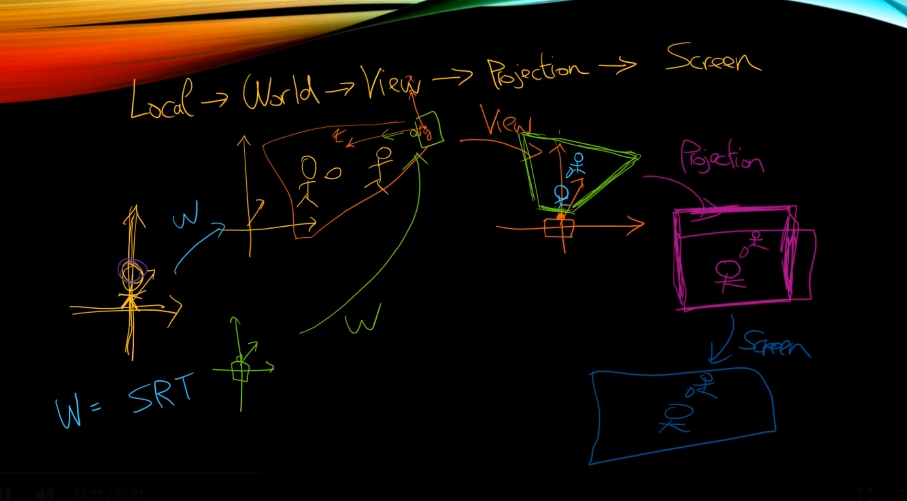
Scene애서 플레이가 다른애 쫒아가는 상황이라고 가정을 하자.

각기 오브젝트마다의 World 변환 행렬은 다르다.

World행렬은 물체마다 독립적으로 다 따로따로 있다.

물체에다가 World행렬을 곱하면 원한 크기, 위치, 각도 위치함.

=> SRT

그다음 카메롸 좌표를 기준으로 View 변환 행렬 연산하고 Projection진행한다 (투영)

그다음 Screen좌표로 바꾸어줌.

2. Local Space <-> World Space

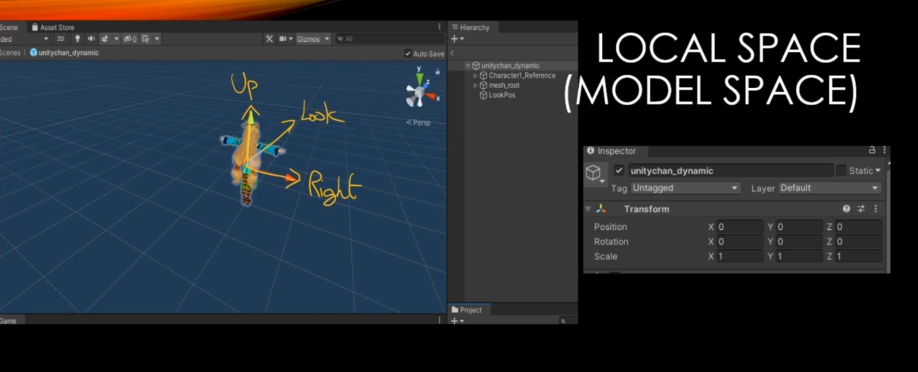
보통은 RightVector, UpVector, LookVector라고한다.

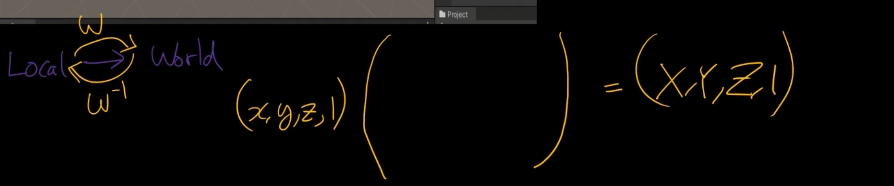
w라는 행렬을 통해서 S <-> W 왔다리 갔다리 가능함.

또한 어떤 좌표 (x, y, z, 1)에 어떤 좌표를 곱하니까 => Wolrd Space좌표로 바꿀 수 있다.

이게 처음 공식임.

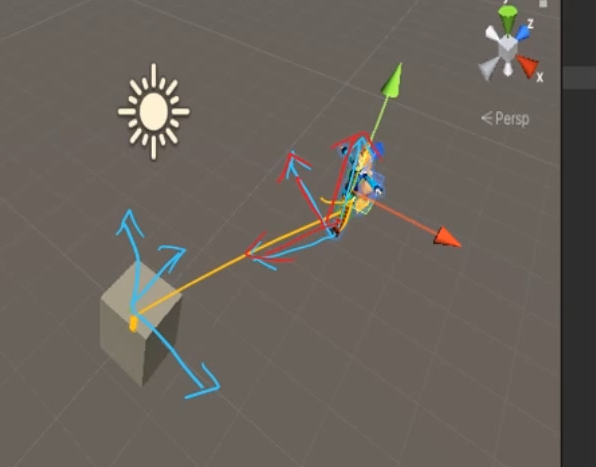
3. 정리

어쨋든 Local Space -> World Space로 변환 시켜주는 Wolrd변환 행렬을 SRT로 구할 것이다.

또한

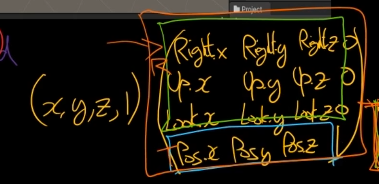
여기서도 정보를 추출 할 수 있다.

4. View Space 변환

Camera Space 변환.

World Space라 함은 Camera를 기준으로한 좌표계라고 보아도 된다.

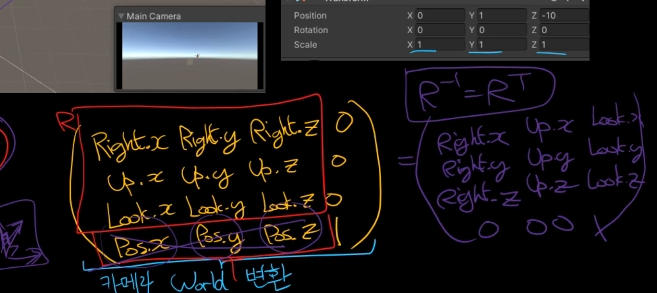
이게 R의 역행렬임.

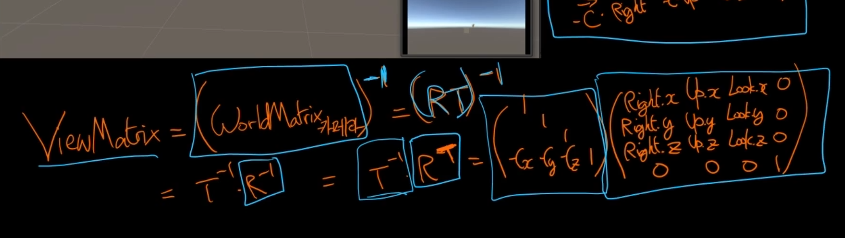
Projection, Screeen 변환 행렬

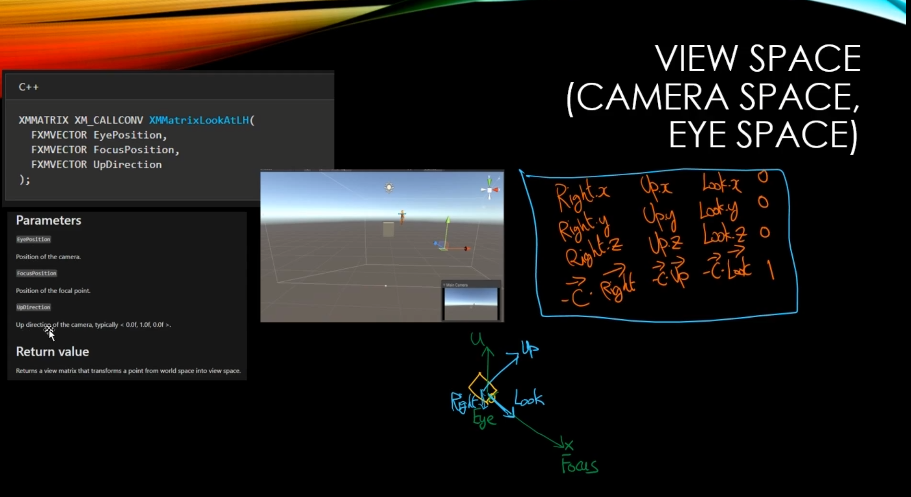
XMatrixLookAtLH라는 함수를 활용을 하면 view변환 행렬을 만들 수 있다.

1. Projection Space

(Homogeneeous Clip Space)

3D -> 2D로 바꾸는 작업 == 투영단계.

원근 투영할 꺼임 => 멀리있는게 작아보이는..

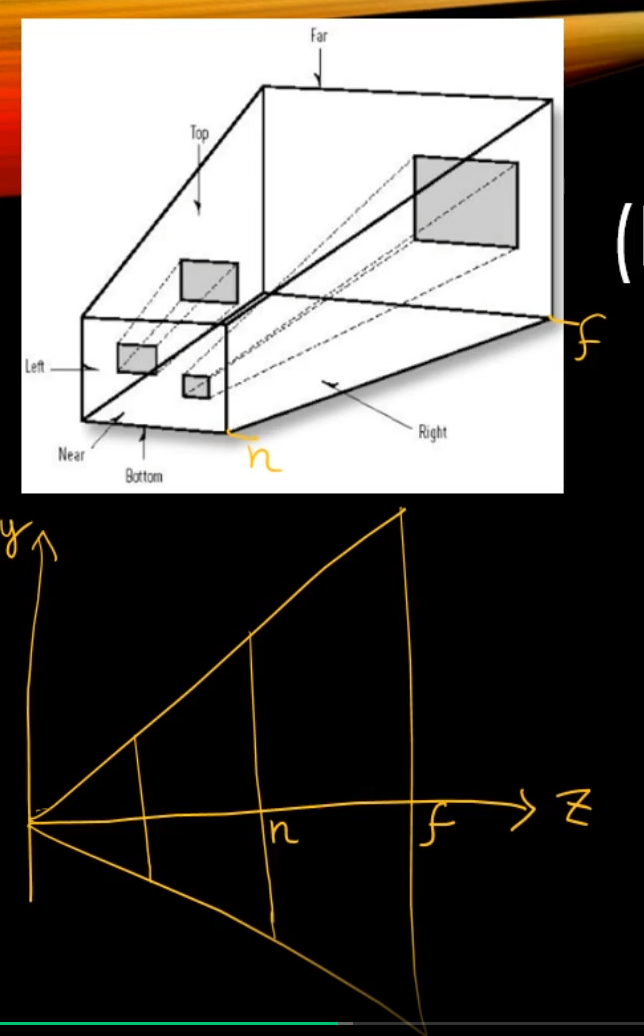
near ~ far에 들어오는 녀석들만 카메라에 투영할 것이다.

상이 맺히는 곳은 near가 아닐 수 있다.

처음에 계산 편하게 하기 위해서 카메라 시야각을 90도로 설정 할 경우와 90도 보다 클 경우

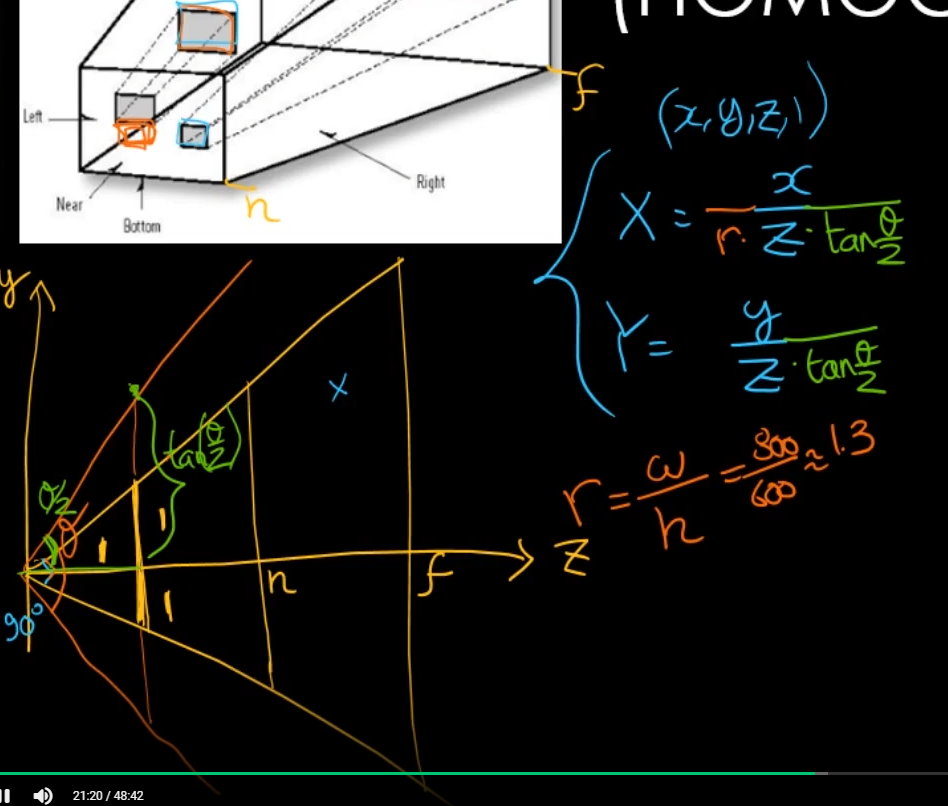
90도 보다 클 경우 늘어난 세타/2의 길이가 2라고 가정을 할 때 1이라는 값에 들어가기를 원하니까 tan 세타/2만큼 나누면됨....

(머선말임?)

Object -> WVP 행렬에 곱해주면 -> 투영됨.

2. Screen Space

(Window Space)

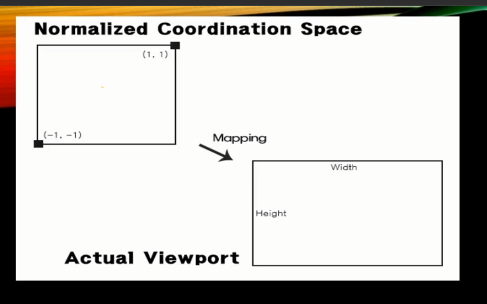
투영까지 되었으니 이제 Screen좌표로 옮기면 끝이다.

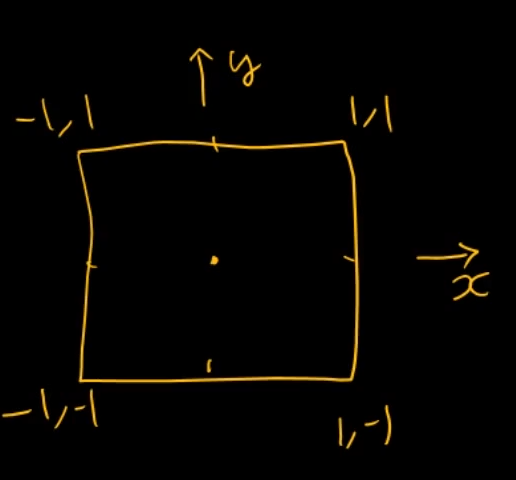
ViewPort란? 렌더링할 화면의 사각영역이다.

ViewPort가 800 x 600이라면은

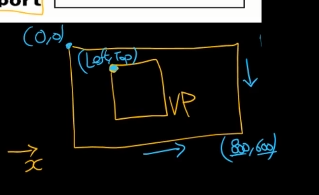
이런식으로 좌표가 잡힌다.