
1
ㅇㅇ.
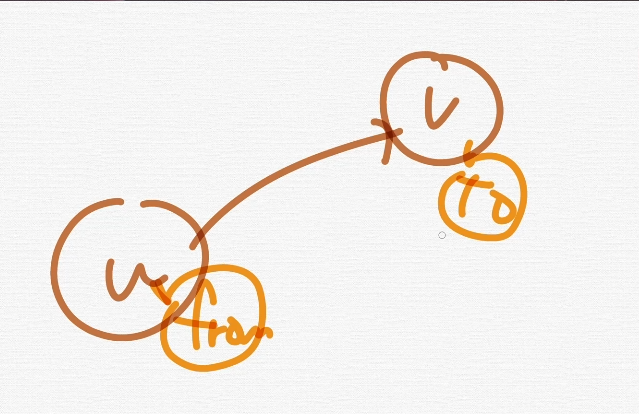
보통 그래프같은데서 u ,v 로 표현을 많이 하는데 이거 u는 from, v는 To이다.
Outdegree, Indegree
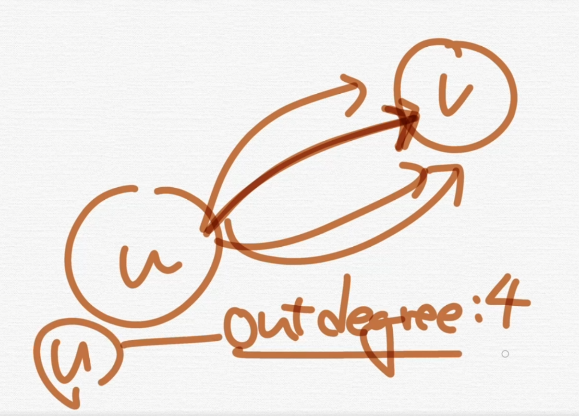
u에서 나가는 단방향 간선이 4개임. 이것을 outdegree가 4개라고 하는 것이다.
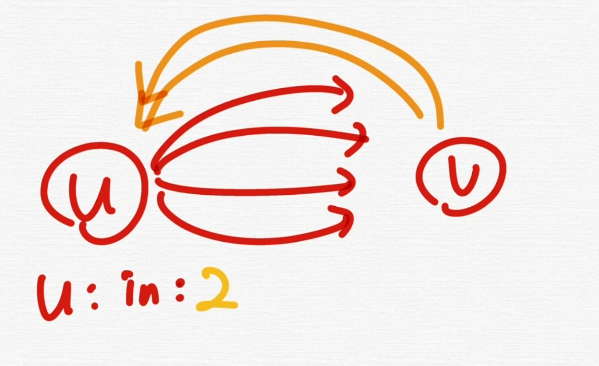
u라는 vertex의 관점에서는 Indegree가 2개 Outdegree가 4개이다.
v라는 정점의 기준에서는 Indegree는 4개이다.
Outdegree는 2개이다.
그래프
이런 정점과 간선이루어진 집합을 "그래프"라고한다.
가중치
정점과 정점사이의 비용
2. 트리
나무를 뒤집은 형태의 자료구조를 "트리"라고함.
트리는 자식노드와 부모노드로 이루어진 계층적인 구조를 가지며 "무방향 그래프"의 일종이자 사이클이 없는 자료구조를 말한다.
트리도 "그래프"임. 단 무방향 그래프
방향성이 없기 때문에.
또한 순환구조 Cycle이 없다.
그래프가 가장 큰 개념이고
트리가 이 그래프의 안에 들어감. 무방향 그래프로 들어감.
트리도 노드와 간선을 가지기 때문에.
트리 특징 ❗
Vertex - 1 = Edge 라는 특징을 가진다.
간선 수 = 노드 수 - 1
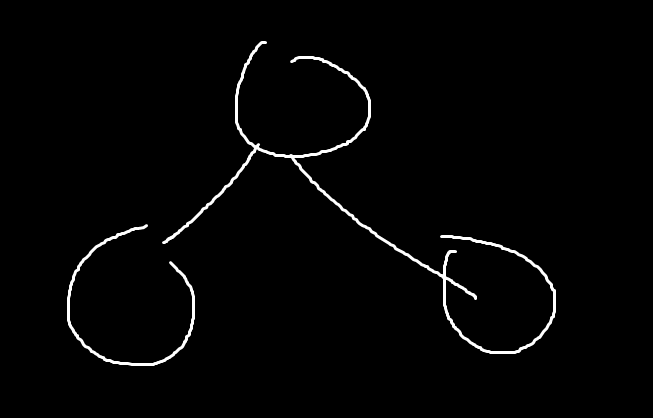
이런 트리가 있으면
V - 1 = E 가 맞나?
3 - 1 = 2 맞다.
또한 "트리" 안에서는 무조건 A노드에서 B라는 노드로 가는 경로가 무조건 존재함.
단, 그래프 일 경우 없을 수도 있음.
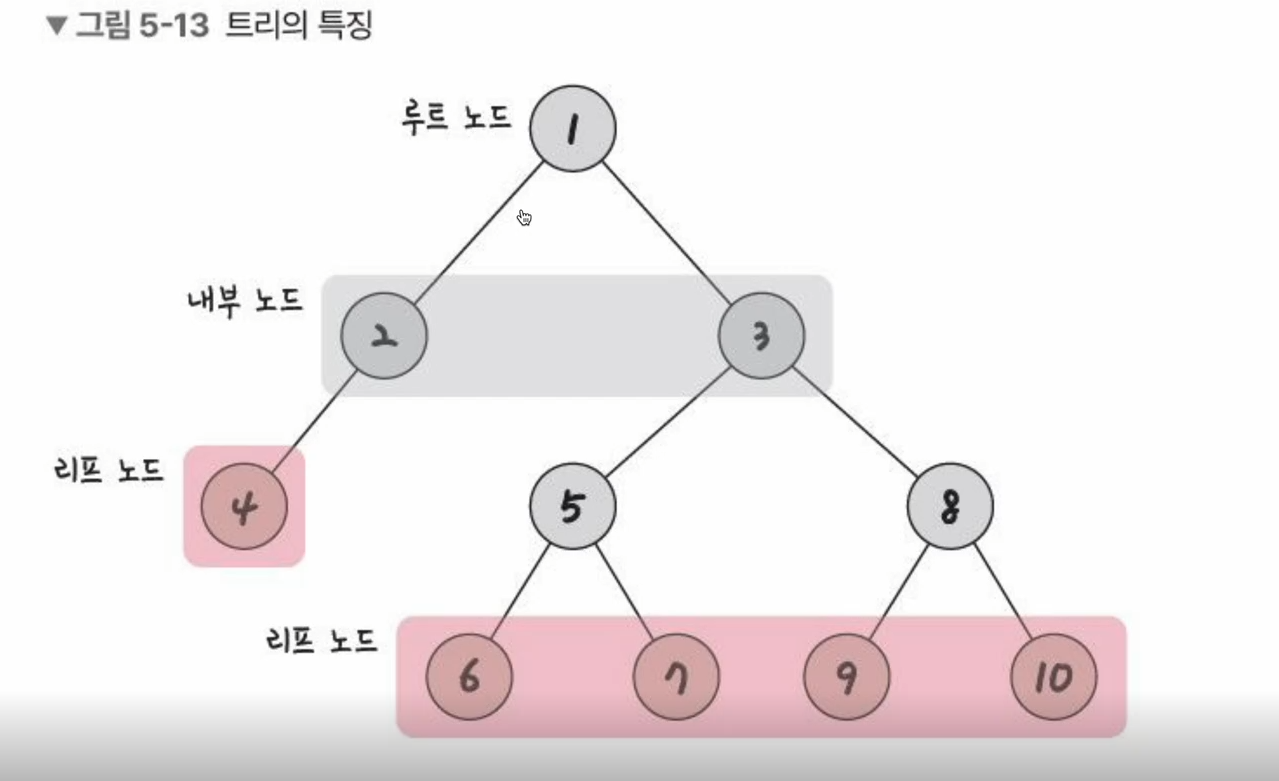
트리는
- 루트
- 내부
- 리프
로 이루어짐.
트리 깊이, 높이

- 깊이
트리에서의 깊이는 각각의 노드마다 다르며, 루트 노드에서 특정 노드까지 최단거리로 갔을 때의 거리를 말한다.
예를 들어 4번 노드의 깊이는 2이다.
-
높이
루트노드부터 리프 노드까지의 거리중 가장 긴 거리를 의미한다.
-
레벨
레벨은 깊이와 비슷한 개념임.
문제마다 조금 다름.
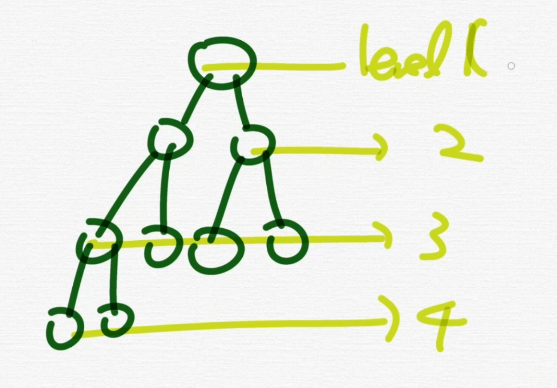
루트를 레벨 0으로 줄 수도 있음.
- 숲
트리로 이루어진 집합을 숲이라한다.

트리 두개 이상일 경우
3. 이진트리, 이진탐색 트리
- 이진트리
각각의 노드의 자식노드 수가 2개 이하로 구성되어있는 트리를 의미하며 다음과 같이 분류함.

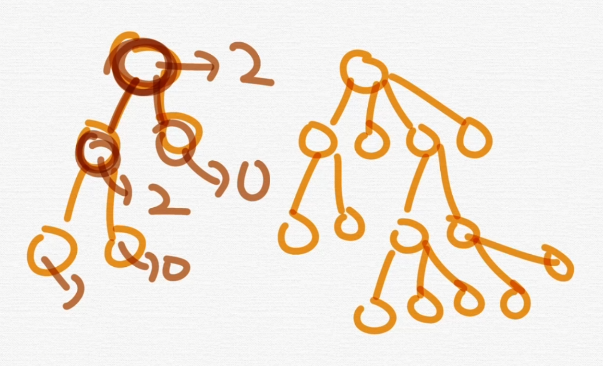
오른쪽도 "트리"임
근데 자식이 2개 이하일 경우 이진트리라고한다.
중간에 완전이진 트리는 "왼쪽"에서부터 다 채워진 이진트리를 완전이진트리 라고한다.

이런것도 이진 트리임. 자식이 두개 이하로 구성되어 있기 때문에.
이딴 모양을 degenerateTree라고한다.
변질이진트리
포화 이진 트리는 왼쪽에서부터 싹다 채워진트리
균형이진 트리
이게 제일 중요함 다섯가지 중에.
모든 노드의 왼쪽 하위 트리와 오른쪽 하위 트리의 차이가 1이하인 트리.
map, set를 구성하는 레드블랙트리는 균형이진 트리중 하나이다.
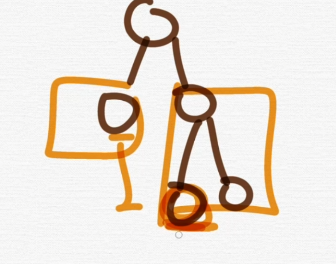
빨간 부분과 왼쪽 리프 노드의 차이가 1임. 이것을 균형이진 트리라고한다.
(이거 구현하는 부분도 배웠었는데 구현하는것은 많이 복잡하고 힘들다 => 거의 못한다)
이진탐색트리 BST
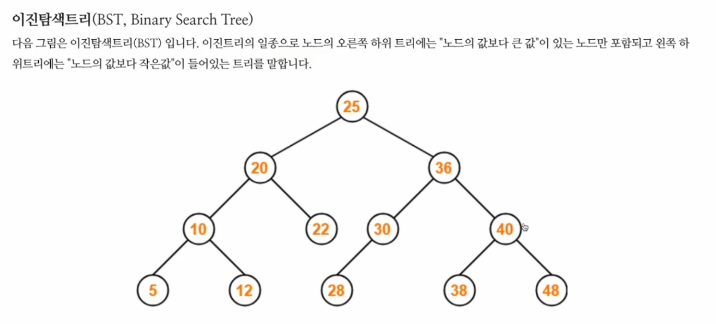
이거 뭔지 알겠제??
오른쪽은 큰값 밀어넣고 왼쪽은 작은값 밀어놓은 트리임.
여기에서 균형을 맞춰주면 Red Black Tree가 된다.
찾는데 시간복잡도는 O(log n)이 걸린다.
삽입/삭제/수정 모두 O(log n)이다.
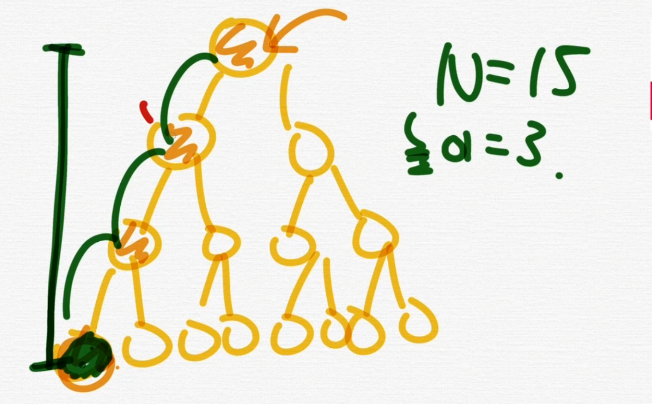
높이는 3이다.
찾는 횟수는 4번만에 초록 노드를 찾을 수 있다.
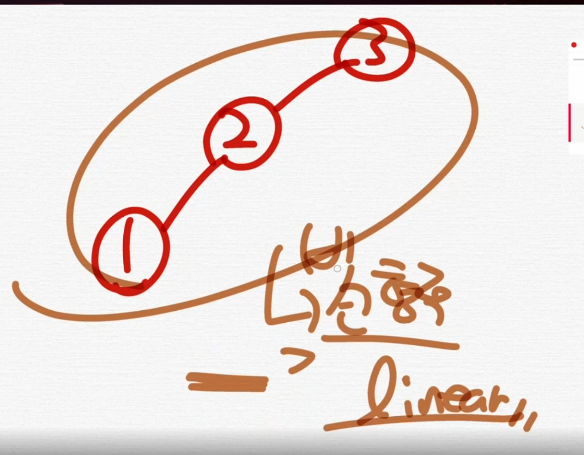
이렇게 선형적 linear 적인 이진트리를 막기위해 균형이진트리가 나온것이다.
이것을 구현을 하는게 Red Black Tree임.
또한 AVL트리도 있음.
우리가 사용하는 자료구조인 map은 red black tree기반이라 시간복잡도가 O(log n)을 보장을 받는다.
4. 인접행렬
내가 생각한 Vertex와 Edge의 집합을 Code로 표현하는 경우 사용되는 두가지 방법이 있다.
그중 하나가
-
"인접행렬"
-
"인접 리스트"
오늘은 인접행렬
인접행렬이란
그래프에서 정점과 간선의 관계를 나타내는 bool 타입의 정사각형 행렬을 의미한다.
단방향과 무방향

일단 개념은 이럼.
무방향은 양방향이기도 하다.
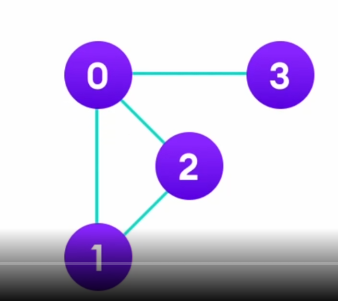
이런그래프는 "무방향 그래프"이다.
그래서 인접행렬이
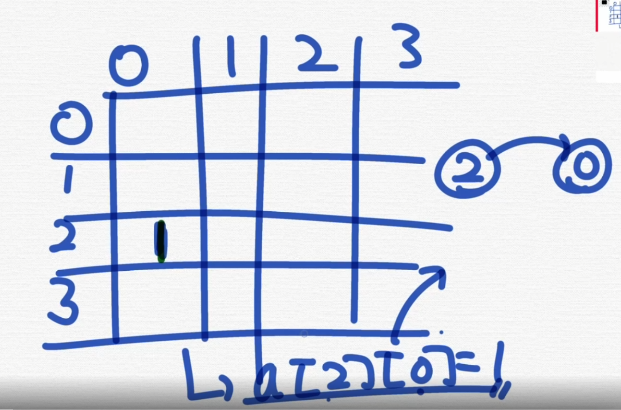
이거말한거임. 이전에 공부했던 것.
인접행렬이 뭘 말하는지 잘 몰라는데 해결됨.

자기 자신은 1또는 0으로 표현하는 경우가 많다.

행을 기준으로 열을 탐색을 한다.
y 를 기준으로 x를 탐색을 한다.
근데 이거 열부터 탐색을 하면 뭐다??
=> "cache" freindly하지 않다❗❗❗
C++에서는 캐시를 첫번째 차원(y를 말함)을 기준으로 하기 때문에 캐시관련 효율성 때문에 탐색을 할 때 주의해야한다.
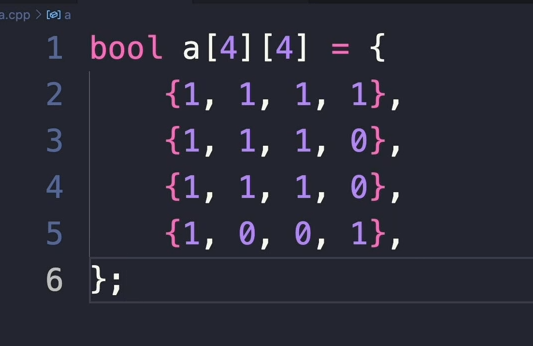
이렇게 만든거를 말한 것이다.
구현 ❗

#include <iostream>
#include <cstring>
#include <vector>
using namespace std;
#define endl "\n"
typedef long long ll;
int arr[10][10] =
{
{0, 0, 0, 0, 0, 0, 0, 0, 0, 0},
{0, 0, 1, 1, 0, 0, 0, 0, 0, 0},
{0, 1, 0, 0, 0, 0, 0, 0, 0, 0},
{0, 1, 0, 0, 1, 0, 0, 0, 0, 0},
{0, 0, 0, 1, 0, 0, 0, 0, 0, 0},
{0, 0, 0, 0, 0, 0, 0, 0, 0, 0},
{0, 0, 0, 0, 0, 0, 0, 0, 0, 0},
{0, 0, 0, 0, 0, 0, 0, 0, 0, 0},
{0, 0, 0, 0, 0, 0, 0, 0, 0, 0},
{0, 0, 0, 0, 0, 0, 0, 0, 0, 0}
};
vector<int> v;
void DFS(int here)
{
v[here] = true;
cout << "Visited : " << here << endl;
for (int there = 0; there < 10; ++there)
{
if (arr[here][there] == 0) continue;
if (v[there] == false) DFS(there);
}
}
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
v.resize(100);
// DFS_ALL();
DFS(0);
return 0;
}나는 일단 이전에 공부했던거 참고해서 이런식으로 만들었는데
#include <iostream>
#include <cstring>
#include <vector>
using namespace std;
#define endl "\n"
const int V = 10;
bool arr[V][V], visited[V];
void go(int from)
{
visited[from] = 1;
cout << from << endl;
for (int i = 0; i < V; ++i)
{
if (visited[i]) continue;
if (arr[from][i]) go(i);
}
return;
}
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
arr[1][2] = 1; arr[1][3] = 1; arr[3][4] = 1;
arr[2][1] = 1; arr[3][1] = 1; arr[4][3] = 1;
for (int i = 0; i < V; ++i)
{
for (int j = 0; j < V; ++j)
if (arr[i][j] && visited[i] == 0) go(i);
}
return 0;
}이렇게 됨. 둘다 뭐 똑같은 코드임.
이게 DFS이다.
5. 인접 리스트
인접 행렬은 2차원 배열을 기반으로 만드는 것이다.
"인접 리스트"는
연결 리스트는 여러개 만들어서 그래프를 표현하는 방식이다.
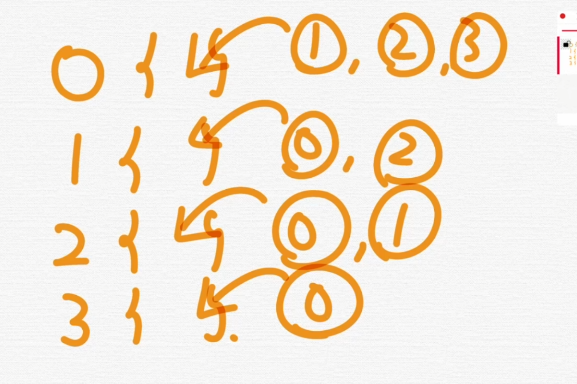
이런식으로 0번에 연결된거, 1번에 연결된거 이런식으로 표현한다.
보통 adj로 표현을 한다.
adj를 4개를 만들어야함.
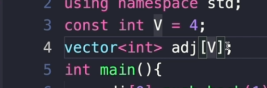
- 4개를 이런식으로 만들었는데 왜 list가 아니라 vector이냐와
vector<int> arr[V];-
이거는 뭐냐?
이거 두가지가 궁금하다.
vector<int> arr[V];이거는 arr이라는 변수는 vector<int> 라는 자료형을 가지는 변수.인데 이게 배열이라는 말이다.

#include <iostream>
#include <cstring>
#include <vector>
using namespace std;
#define endl "\n"
int V = 10;
vector<vector<int>> vec;
vector<bool> visited;
void CreateGraph()
{
vec = vector<vector<int>>(V);
visited.resize(V);
vec[1].push_back(2);
vec[2].push_back(1);
vec[1].push_back(3);
vec[3].push_back(1);
vec[3].push_back(4);
vec[4].push_back(3);
}
void DFS(int here)
{
visited[here] = true;
cout << "Visited : " << here << endl;
for (int i = 0; i < vec[here].size(); ++i)
{
int there = vec[here][i];
if (visited[there] == false)
DFS(there);
// 위와 같은 코드임
/*if (visited[here]) continue;
DFS(there);*/
}
}
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
CreateGraph();
DFS(1);
return 0;
}이렇게 인접 리스트를 통해서 그래프를 만들고 이것을 DFS로 탐색을 하는 부분이다.
DFS까지는 뭐 아직 쉬운거 같다.
정리하자면
인럽 행렬은 2차원 배열을 기반으로 그래프를 만든 것이고
인접리스트는 연결형 리스트로 만드는 것인데
연결리스트보다 vector가 시간복잡도나 cache friendl한 장점이 많기 때문에 vector를 사용해서 인접리스트를 구현해도 무방함.
(+자료구조를 공부 조금만 했다면 금방 이해할듯?)
6. 인접리스트 vs 인접행렬
공간 복잡도
시간 복잡도

그래프가 dense할 경우 인접행렬이 좋고,
그래프가 sparse할 경우 인접 리스트가 좋다.
그래서 둘중 뭘 쓸까??

보통 거의다 인접리스트 사용하면된다.
dense한 경우가 그렇게 많이 나오지 않는다.
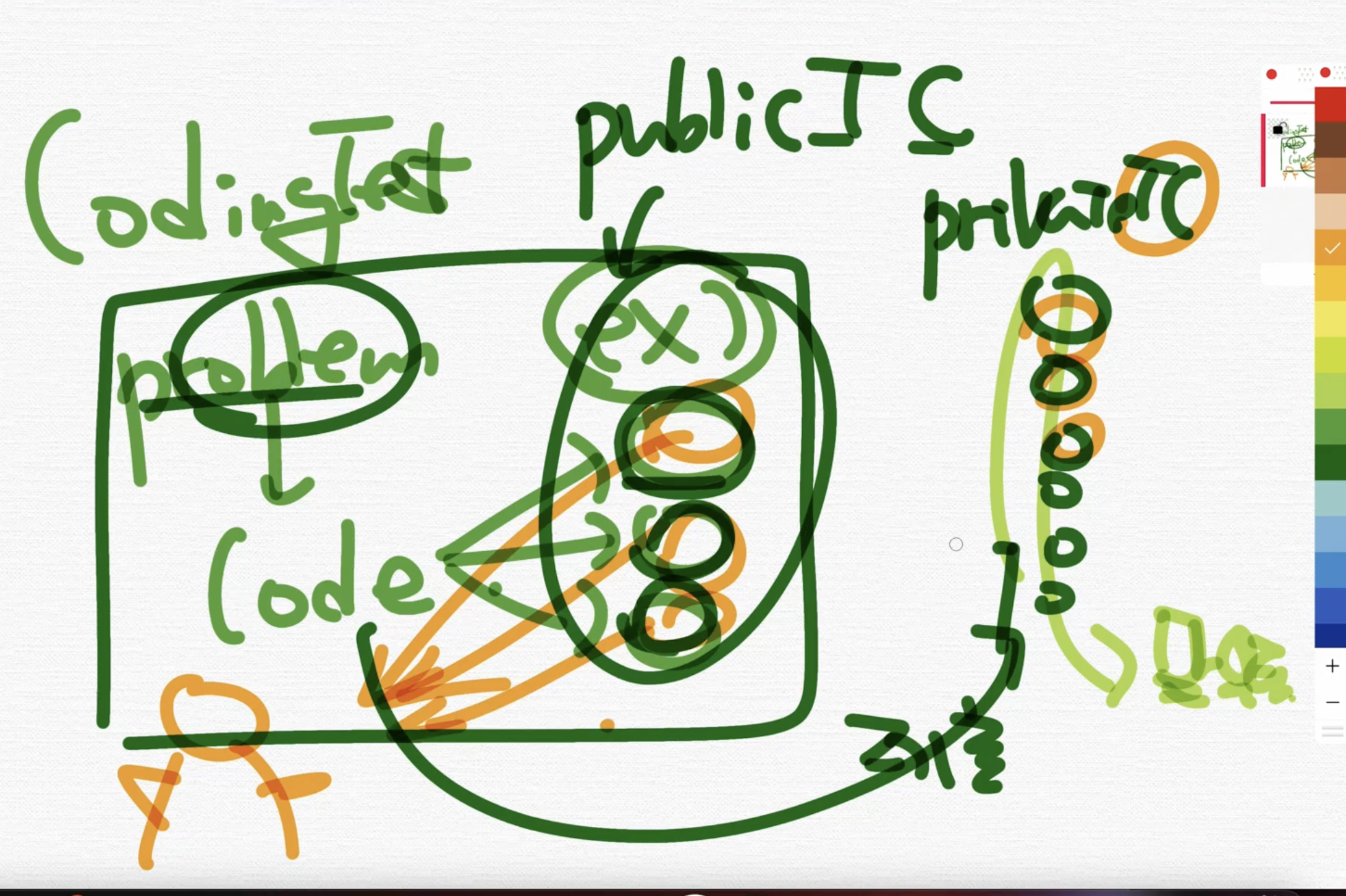
출제하는 사람이 TC를 먼저 준다. 그리고 TC를 통과를 하면은 private한 TC통과를 하는지 않하는지를 본다.
근데 private한 TC도 사람이 만들기 때문에 dense한 그래프를 잘 출제를 안한다. (자기내 들도 틀릴 수가 있기 때문에)
7. map과 방향 벡터
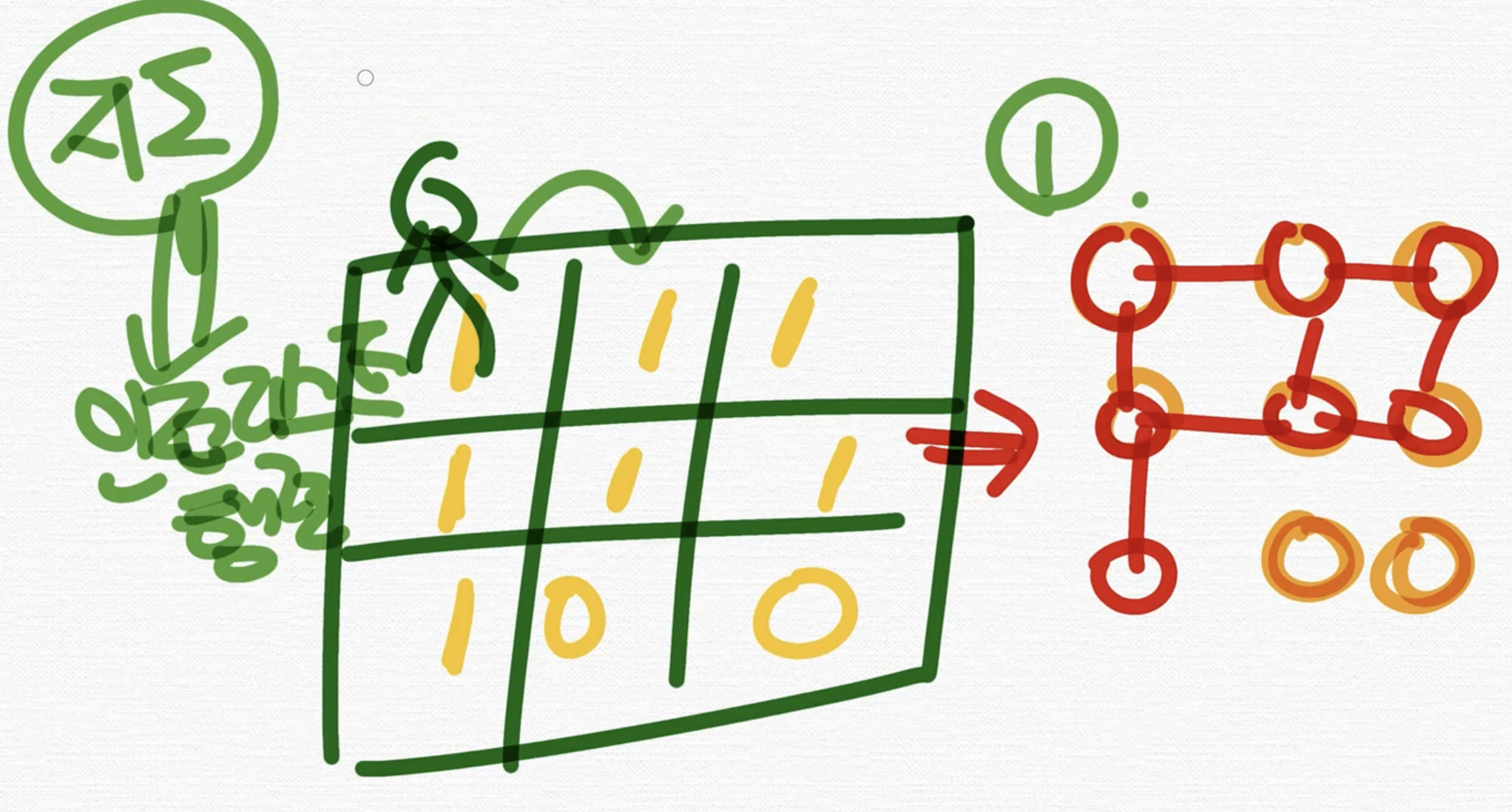
이런 map과 관련된 문제가 나오면 간선을 생각할 수 있지만 이것을 인접리스트나 인접행렬로 바꾸어서 풀면 안되고 지도를 기반으로 그냥 풀어야 된다.
이거 구현해봐라

이전에 배웠던 dy, dx를 사용을 해주도록 하자.
#include <iostream>
#include <vector>
using namespace std;
const int dy[4] = {0, -1, 0, 1};
const int dx[4] = {-1, 0, 1, 0};
const int ms = 3;
int arr[ms][ms];
int v[ms][ms];
bool Cango(int y, int x)
{
if (y < 0 || y > ms || x < 0 || x > ms)
return false;
else
return true;
}
void go(int y, int x)
{
v[y][x] = 1;
cout << y << ", " << x << endl;
for (int i = 0; i < 4; i++)
{
int ny = y + dy[i];
int nx = x + dx[i];
if (Cango(ny, nx) == false) continue;
if (arr[ny][nx] == 0) continue;
if (v[ny][nx] == 1) continue;
go(ny, nx);
}
}
int main()
{
for (int i = 0; i < ms; ++i)
{
for (int j = 0; j < ms; ++j)
cin >> arr[i][j];
}
go(0, 0);
return 0;
}위의 코드는 3x3 짜리 map에서 입력을 받고 어느곳으로 가고 갈 수 없는지를 재귀함수로 구현을 한 코드이다.
주의 해야 할점
현재 Cango가 제일 앞에 와야 하는 이유는 배열의 인덱스를 넘어서는지 아닌지부터 체크를 항상 해야한다.
만약 for문 안에서 Cango가 다른 if문 보다 뒤에 있다면 arr[ny][nx]참조하는 과정에서 Index out of Range를 발생할 수 있기 때문이다.
8. 연결된 컴포넌트
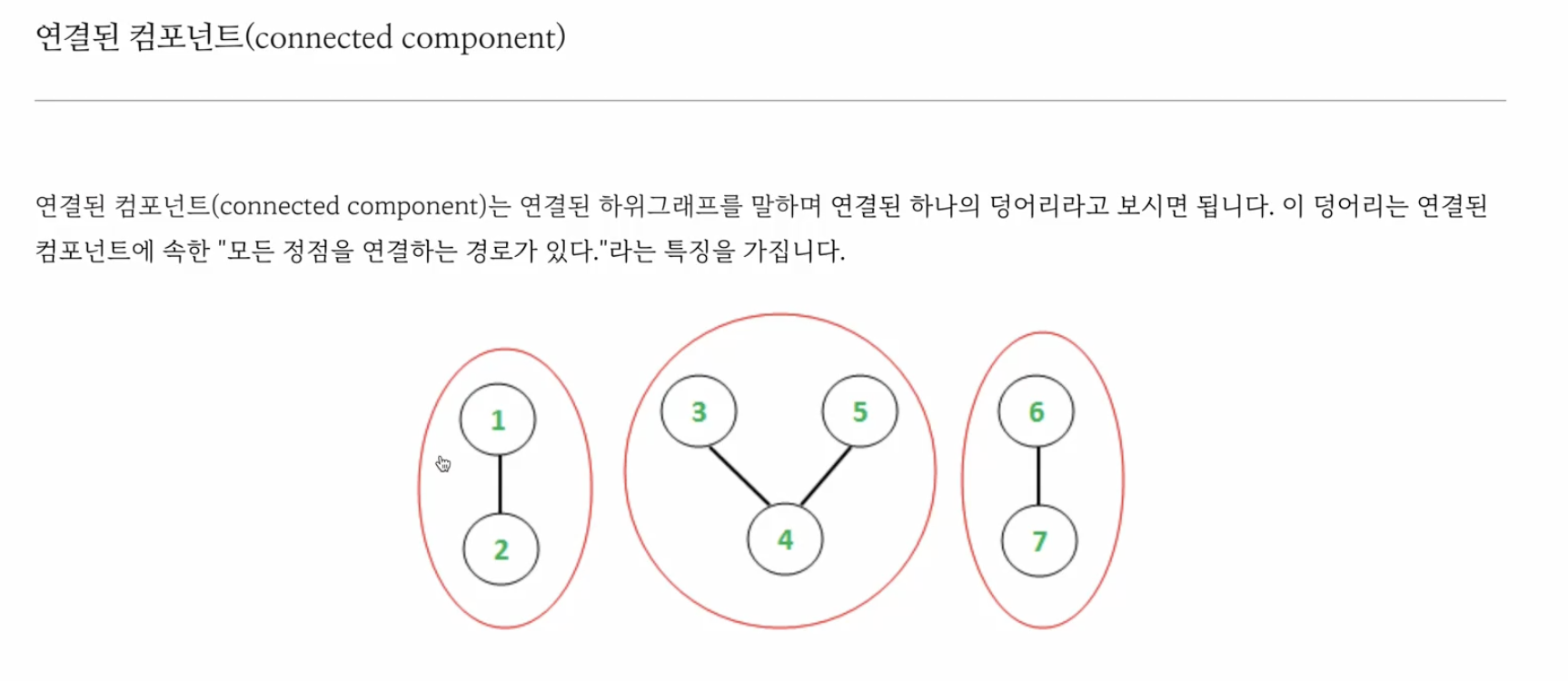
여기서는 연결된 컴포넌트의 갯수는 3개이다.
그냥 연결된 vertex와 edge를 한 덩어리로 갯수를 세면된다.
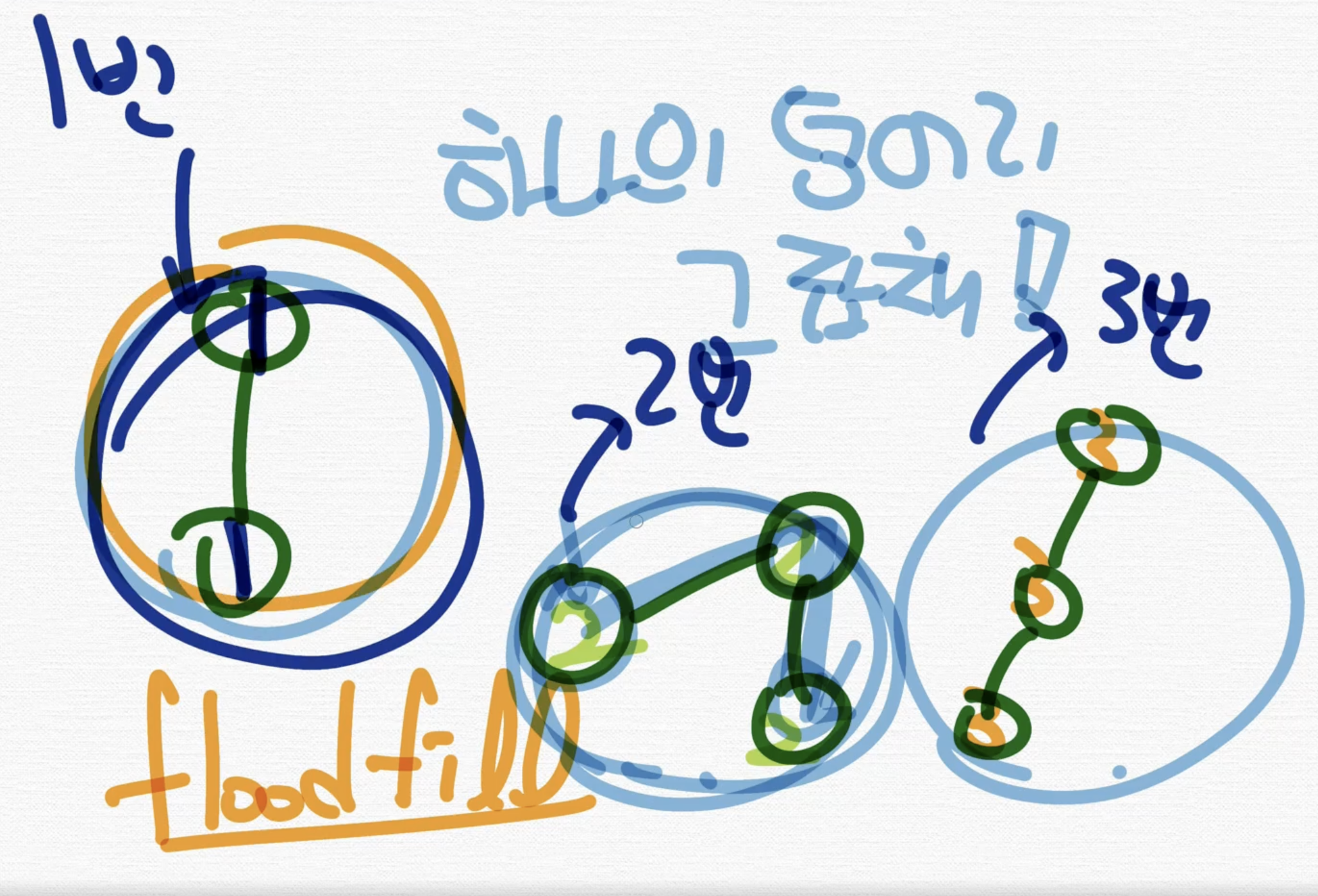
이런 덩어리들끼리 나누어서 번호를 매기는 것을 "floodfill"이라는 알고리즘이라고 한다.
이전시간에 map주면서 이것을 재귀함수로 구현을 해보았었는데
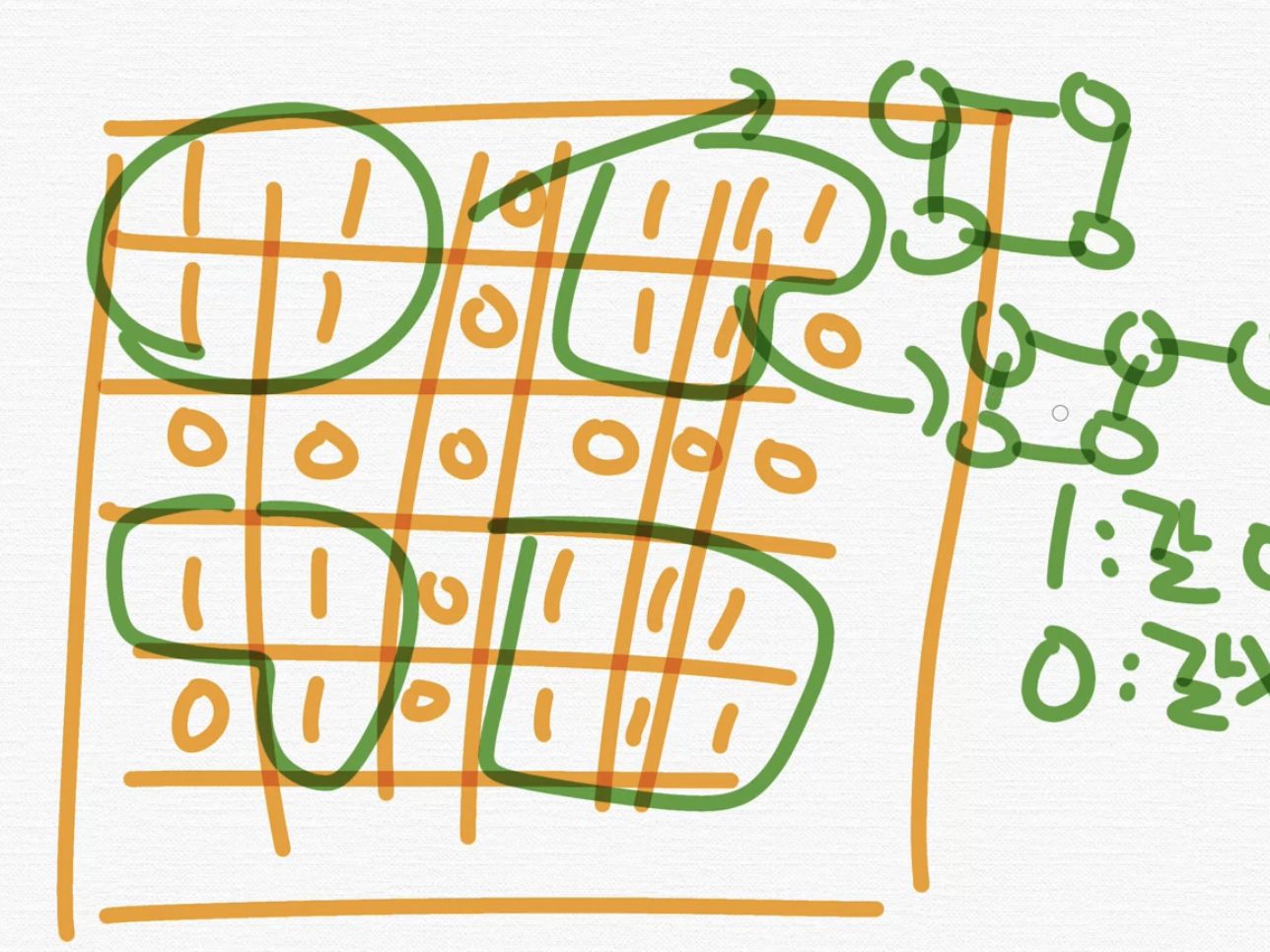
마찬가지로 큰 map이 주어질 때 이것을 floodfill로 만들 수 있다.
갈 수 있는 부분들을 하나의 집합을 만들어서 한덩어리, 한덩어리 이렇게 구분이 가능하다.

이것을 한덩어리 한덩어리 connected component로도 생각을 해보아야한다.
9. DFS
개념은 뭐 이전에도 몇번 해서 아직 기억이 난다.
Depth First Search이다.
DFS를 구현을 하는 방법은 두가지이다.
- 돌다리 두드리기
- 못먹어도 GO
돌다리
void DFS(int here)
{
visited[here] = true;
cout << "Visited : " << here << endl;
for (int i = 0; i < vec[here].size(); ++i)
{
int there = vec[here][i];
if (visited[there] != true) DFS(there);
}
cout << here << "로 부터 시작된 함수가 종료 되었습니다." << endl;
return;
}이런식으로 먼저 확인을 하고 건너는 방법과
GO
못먹어도 GO
void DFS(int here)
{
if (visited[here]) return;
visited[here] = 1;
for (int there : vec[here])
{
DFS(there);
}
}이런식으로 구현할 수 있는데 때에 따라서 두가지 방식중 하나를 골라야한다.
문제

이 문제는 connected component를 찾는 문제이기는 하다.
일단 내가 구현한 부분은
#include <iostream>
#include <cstring>
#include <vector>
using namespace std;
#define endl "\n"
vector<vector<int>> vec;
vector<vector<bool>> visited;
int n, m, cnt = 0;
int dy[4] = {0, 1, 0, -1};
int dx[4] = {-1, 0, 1, 0};
void CM()
{
cin >> n >> m;
vec.resize(n);
visited.resize(n);
for (int i = 0; i < n; ++i)
{
vec[i].resize(m);
visited[i].resize(m);
}
for (int i = 0; i < n; ++i)
for (int j = 0; j < m; ++j) cin >> vec[i][j];
}
bool Cango(int y, int x)
{
if (y < 0 || y >= n || x < 0 || x >= m) return false;
return true;
}
void go(int y, int x)
{
visited[y][x] = true;
cout << y << ", " << x << endl;
for (int i = 0; i < 4; ++i)
{
int ny = y + dy[i];
int nx = x + dx[i];
if (Cango(ny, nx) == false) continue;
if (visited[ny][nx] == true) continue;
if (vec[ny][nx] == 0) continue;
go(ny, nx);
}
}
void goAll()
{
for (int y = 0; y < vec.size(); ++y)
{
for (int x = 0; x < vec[y].size(); ++x)
{
if (vec[y][x] == 0) continue;
if (visited[y][x] == true) continue;
go(y ,x);
++cnt;
}
}
}
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
CM();
goAll();
cout << cnt << endl;
return 0;
}이렇게 구현을 하였다.
중간에 계속 에러 났던 부분은 Cango함수의 if문으로 범위 체크 하는 부분에서 y > n이 아니라 인덱스 이기 때문에 y >= n 일 경우로 다 바꿔주었다.
10. BFS
- BFS
그래프를 탐색하는 알고리즘이며 어떤 정점에서 시작해 다음 깊이의 정점으로 이동하기전 현재 깊이의 모든 정점을 탐색하며 바운한 정점은 다시 방문하지 않는 알고리즘이다.
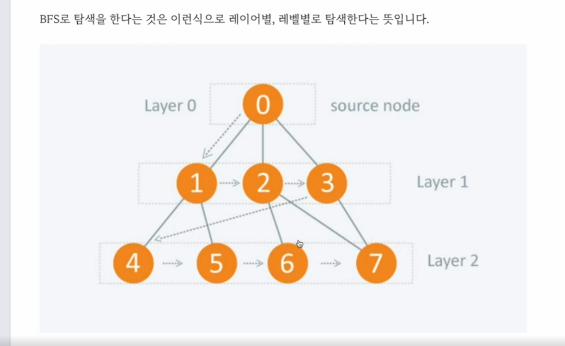
Level별로 탐색을 한다.
즉 다시 정리를 하자면은 BFS는
그래프를 탐색하는 알고리즘이며 정점에서 시작해 다음 깊이의 정점으로 이동하기 전 현재 깊이의 모든 정점을 탐색하며 방문한 정점은 다시 방문 하지 않는 알고리즘이다. 같은 가중치를 가진 그래프에서 최단거리 알고리즘으로 쓰인다.
중요한 것은 "가중치"가 같다라는 점과 한번 방문한 곳은 방문하지 않는다는 부분이다.
가중치가 같기 때문에 가중치를 표현못하는 한계가 있어서 "다익스트라" 라는 알고리즘이 있따. 다익스트라
void BFS(int here)
{
queue<int> q;
visited[here] = 1;
q.push(here);
while(!q.empty())
{
int here = q.front(); q.pop();
for (int there : adj[here])
{
if (visited[there]) continue;
visited[there] = visited[here] + 1;
q.push(there);
}
}
}코드는 이런데
알아야 할점
-
최단거리
visited가 "최단거리" 의미한다.
그래서 A노드부터 B노드까지 거리는? 라고 하면은
visited[] 여기 B를 넣고 -1 을 해주면된다.
(2칸이라면 그냥 * 2 해버리면됨) -
시작점이 다수일 때
일단 무조건 시작점은 visited를 1로 놔두어야한다.

아까랑 똑같이 for도는데 visited를 1로 해주면된다.
-
방문처리만 하는 BFS
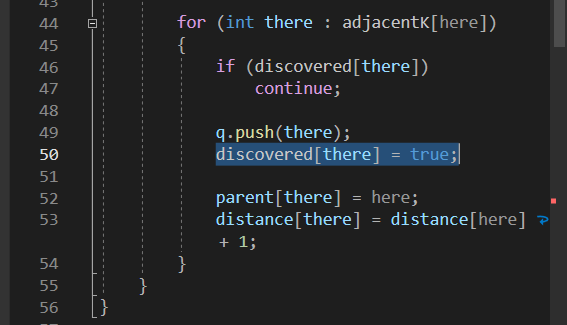
Ro 강의에서는 이런식으로 방문처리만 했었는데 보통 문제에서는 최단거리를 찾아라고 하기 때문에
이런식으로 visited[there] = visited[here] + 1; 로 해주는것이 좋다.
문제 구현 ❗
이 문제 못풀기는 했는데 또 생각 해야하는 부분이 map문제일 경우에는 dy, dx를 사용해야한다.
즉, y, x 축 좌표를 사용하는 문제는 상하좌우 갈수 있는지 없는지를 판별할 수 있는 배열 두개와 BFS를 같이 사용해야한다.
나는 BFS를
void BFS(int y, int x)
{
visited[y][x] = 1;
q.push(pair<int, int>(y, x));
while (!q.empty())
{
pair<int, int> here = q.front();
q.pop();
for (int there : adj[here.first])
{
if (visited[here.first][there]) continue;
visited[here.first][there] = visited[here.first][here.second] + 1;
q.push(pair<int, int>(here.first, there));
}
}
}이런식으로 구현했는데 이렇게 하는게 아니라
#include <iostream>
#include <queue>
#include <vector>
using namespace std;
#define endl "\n"
#define Dir 4
int n, m, sy, sx, dsty, dstx;
int adj[101][101];
int dy[4] = {0, 1, 0, -1};
int dx[4] = {-1, 0, 1, 0};
vector<vector<int> > visited;
queue<pair<int, int> > q;
bool Cango(int y, int x)
{
if (y < 0 || y >= n || x < 0 || x >= m || adj[y][x] == 0)
return false;
return true;
}
void BFS(int y, int x)
{
visited[y][x] = 1;
q.push({y, x});
while (!q.empty())
{
pair<int, int> here = q.front();
q.pop();
for (int i = 0; i < 4; ++i)
{
int ny = y + dy[i];
int nx = x + dx[i];
if (Cango(ny, nx) == false) continue;
if (visited[ny][nx]) continue;
visited[ny][nx] = visited[y][x] + 1;
q.push({ny, nx});
}
}
}
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
cin >> n >> m;
cin >> sy >> sx;
cin >> dsty >> dstx;
visited = vector<vector<int>>(n);
for (int i = 0; i < n; ++i) visited[i].resize(m);
for (int i = 0; i < n; ++i)
for (int j = 0; j < m; ++j) cin >> adj[i][j];
BFS(sy, sx);
for (int i = 0; i < n; ++i)
{
for (int j = 0; j < m; ++j)
{
cout << visited[i][j] << " ";
}
cout << endl;
}
return 0;
}일단 이런식으로 최종 코드가 나왔는데 이거 수정 해야한다. 어딘가 잘못됨.
주의 점 ❗
BFS코드를 보면은 한번씩 코드 앞 부분에
void BFS(int y, int x)
{
q.push({y, x});이런식으로 visited에다가 1을 안거는 코드가 있는데
이렇게 되면은 아래의 상황처럼

시작점이 0으로 방문 처리가 되어있지 않다고 되어있기 때문에 시잠이 필요한 경우 시작점에 대한 로직을 또 따로 만들어 주어야한다.
11. DFS BFS 비교
시간복잡도는 차이가 없다.
만약 둘다 연결리스트로 이루어져있다면은 O(V+E)이고,
인접행렬의 경우 O(V^2)가 된다.

최단거리를 찾을 경우에는 보통 BFS를 사용을 하고,
절단점이나 완전탐색을 해야하는 경우에는 DFS를 사용을 한다.
12. 트리순회
후위/전위/중위 순회
- 트리 순회
트리 구조에서 각각의 노드를 정확히 한번만, 체계적인 방법으로 방문하는 과정을 말한다. 이는 노드를 방문하는 순선에 따라 후위/전위/중위/레벨 순회가 있다. 보통 설명할 때는 이진트리를 기반으로 설명을 한다.
이진 트리란?
자식 노드가 두개 이하인 트리를 말한다.
후위 순회


수도코드가 재귀함수로 구현되어있음.
왼쪽 자식 -> 오른쪽 자식 -> 나 자신 순서이다.
void postOrder(int here)
{
if (visited[here] == 0)
{
if (adj[here].size() == 1) postOrder(adj[here][0]);
if (adj[here].size() == 2)
{
postOrder(adj[here][0]);
postOrder(adj[here][1]);
}
visited[here] = 1;
cout << here << endl;
}
}전위 순회
먼저 자신의 노드를 방문하고 그 다음 노드들을 방문하는 것을 말한다(DFS를 생각하면된다)
void preOrder(int here)
{
if (visited[here] == 0)
{
visited[here] = 1;
cout << here << endl;
if (adj[here].size() == 1) preOrder(adj[here][0]);
if (adj[here].size() == 2)
{
preOrder(adj[here][0]);
preOrder(adj[here][1]);
}
}
}중위 순회
std::map이 중위 순회 도는거는 알제?
왼쪽 노드 -> 나 자신 -> 오른쪽 노드

void inOrder(int here)
{
if (visited[here] == 0)
{
if (adj[here].size() == 1)
{
inOrder(adj[here][0]);
visited[here] = 1;
cout << here << endl;
}
else if (adj[here].size() == 2)
{
inOrder(adj[here][0]);
visited[here] = 1;
cout << here << endl;
inOrder(adj[here][1]);
}
else
{
visited[here] = 1;
cout << here << " ";
}
}
}레벨 순회
이거 그냥 BFS룰 생각을 하면은 된다.

