
상수 시간
Big O 표기법은 알고있었는데
예전부터 상수시간 복잡도? 이부분에서 뭐가 상수시간이라는 건지 햇갈렸음..
엄밀히 말하면 상수시간이 아니겠지만
Big O 표기법으로 아래와 같은 애들을 상수시간 복잡도 O(1)을 가진다고한다.
그냥 간단한 연산이나 비교같은 부분들? 정도
-
상수 시간 복잡도 O(1)
입력크기와 상관없이 일정한 시간 복잡도를 가지는 것을 말한다.
-
ex)
1 입력과 출력 cin, cout, scanf, printf
2 곱하기 : 나누기, 나머지 연산 등등
3 간단한 if문
4 배열 인덱스 참조
Q1
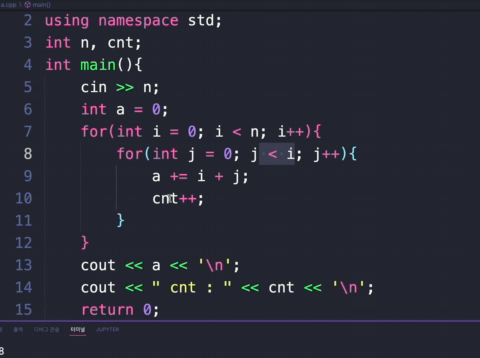
이거 시간복잡도 구해봐라

시간 복잡도는 1/2(n^2 - n)이다.
처음에 N^2이라고는 생각을 했는데
사각형을 그려서 떠올리는 생각은 못함.
Q2
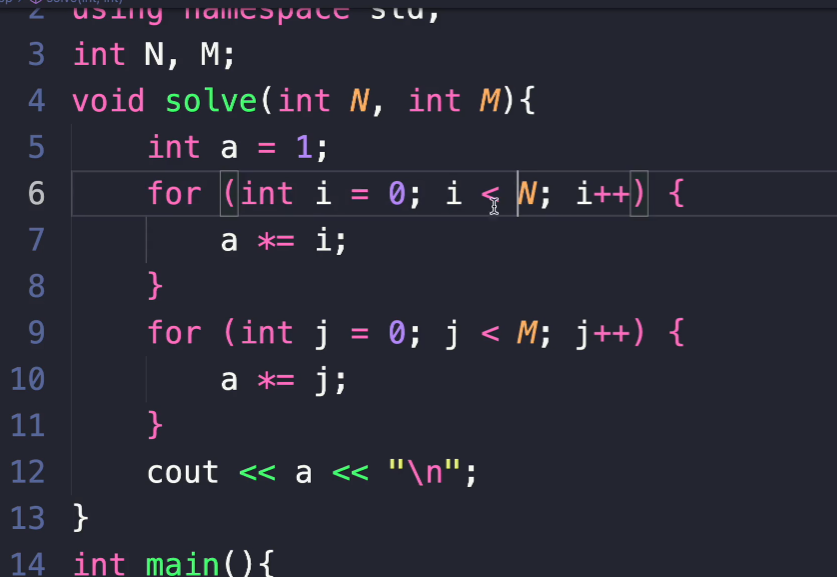
이거 시간 복잡도 구해라
O(n) + O(n)이라 2 * O(n) => O(n)이다.

이거 빅오로 나타내면 O(N^2 + M^2) 일거같다.(ㅇㅇ 맞음)
Q3 ❗

이거 시간 복잡도는?
=> 그냥 일단 직감적으로는 O(log n)이다.
반씩 쪼개니까..
위에 틀렷다 시간은 2n - 1을 가진다.
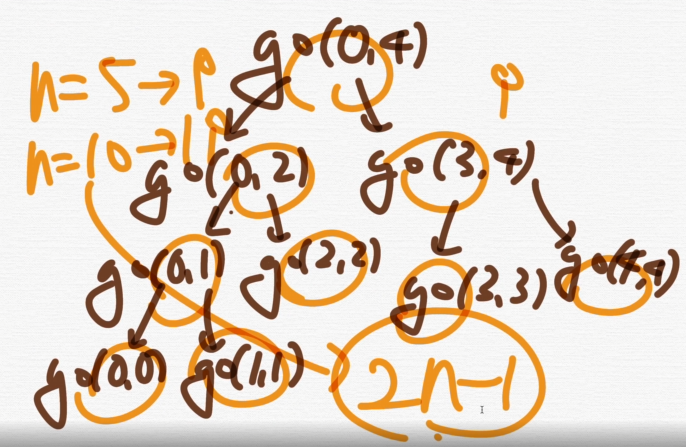
빅오는 O(N)임.
Q4
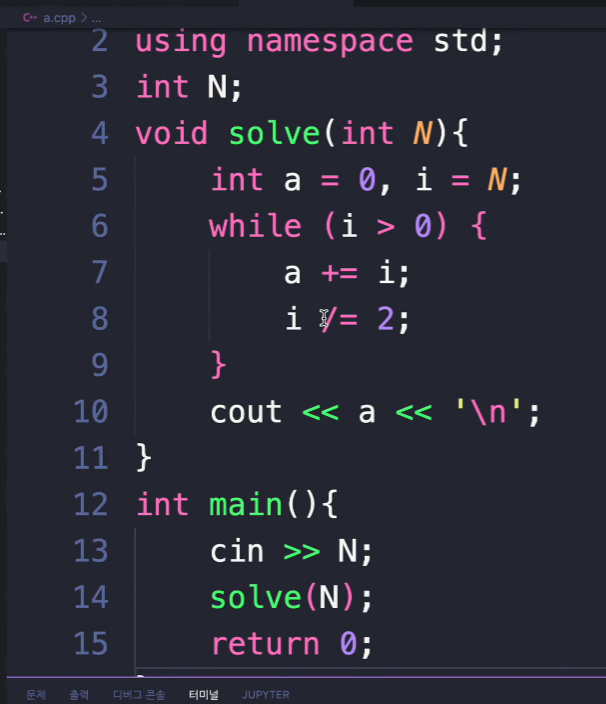
이거 시간 복잡도는?
여기서 O(log n)이 나오네..
절반씩 i가 줄어드니까.
log
log는 지수함수의 역함수이다.
어떤 수를 나타내기 위해 고정된 밑을 몇번 곱하여야 하는지를 나타낸다고 볼 수 있다.
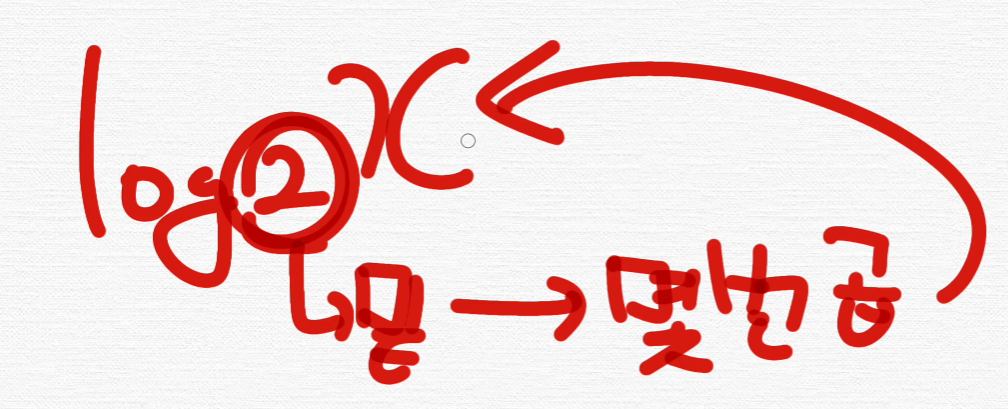
2를 몇번 곱해야 x가 되는지를 log 2 x로 표현을 함.
그래서 계속 2로 나누니까 log n임.
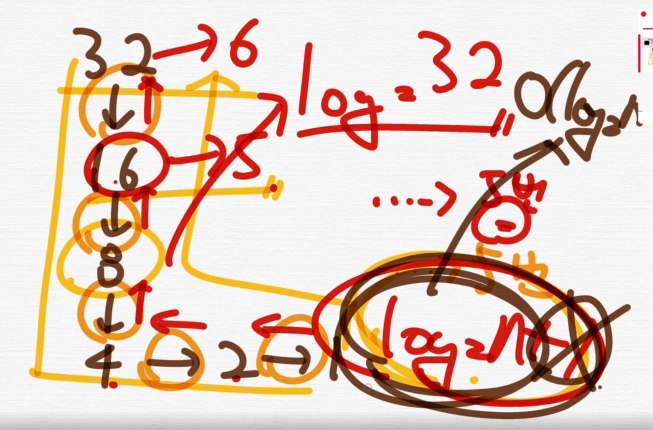
Q5 ❗
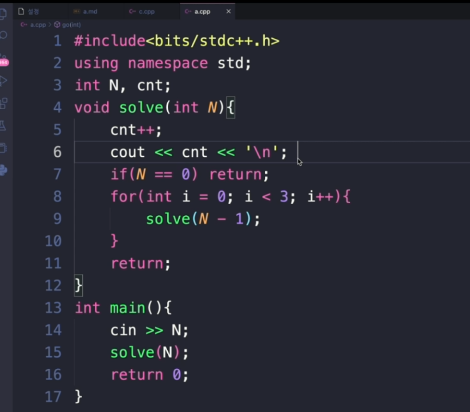
이거 시간복잡도?
❌ 모르겠다.
힌트
등비수열의 합이 힌트이다.

비가 늘어나는 항.
첫항이 3, 공비가 3, 횟수는 N이니까
Sn = 3 * (3^n - 1) / (3 - 1)
Sn = (3^(n+1) - 3) / 2
반복횟수는 (3^(n+1) - 3) / 2회이다.
재귀함수의 시간복잡도 구하는 방법 ❓
재귀함수의 시간복잡도는
"Main Logic * 함수 호출 쵯수" 이다.
시간복잡도
그래서 그냥 N이 3일때도 계산해보고 N일때 계산을 하면 시간복잡도는
O(3^N)이다.
야매 이해 (팁)❓❓❓ 👍👍👍
함수 하나당 반복문 호출 횟수를 4이라고 하면은
함수가 호출되는 시간 복잡도는 O(4^n)이다.

만약 i < 10이라면은
10^n 이된다.
시간복잡도만 구하면 되니까 다시 등비수열 구해보면은

이렇게됨. 이렇게되는 이유는
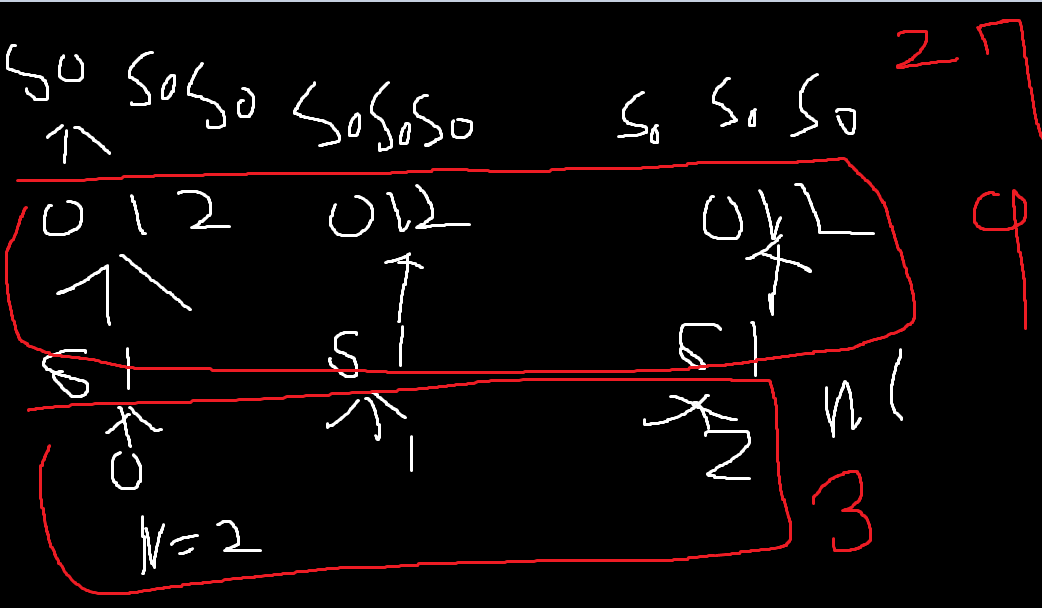
위의 그림처럼 n == 2일 경우에도 이런식으로 호출을 함.
함수하나당 반복문이 3번 돌기 때문에
5라면은
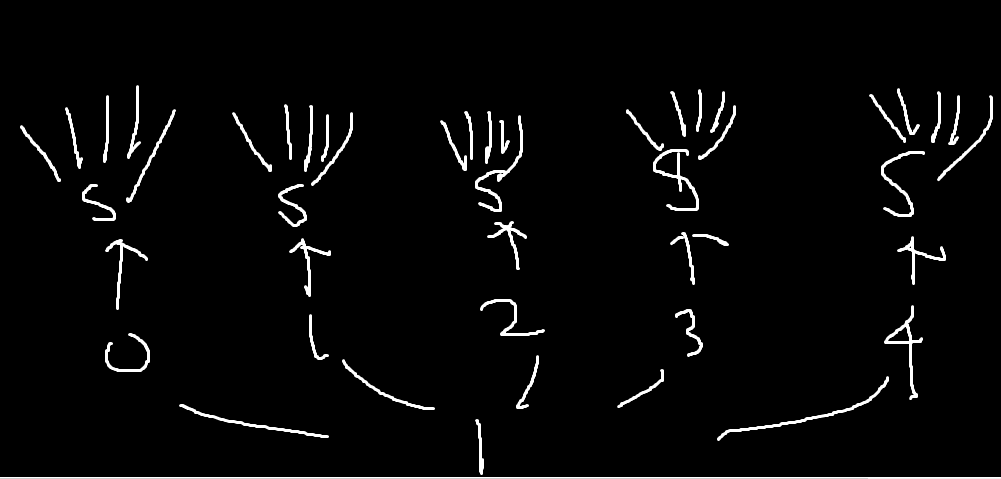
이렇게 5개씩 뻗어나가니까
초항 1이고 공비가 5임.
그림 보면은 처음 1 -> 5 -> 25 ... -> 이런순임.
ㅇㅋㅇㅋ??

