1. WHY?
- 왜 쓰는지에 대해 이해하는 것이 중요하다.
- BFS, DFS 용어에서 유추가 되듯이 먼저,
탐색(Search)에 대해 생각해 볼 필요가 있다.
1.1 탐색(Search)
- 알고리즘을 시작하면서 쉽게 접하게 되는 주제이다.
- 단순히 이름 그대로 원하는 데이터를 검색하는데 최적으로 도달하기 위한 기법이라고 하기에는 다양한 문제(분야)에 접목이 된다. ( 위키피디아 - 검색 알고리즘 )
- 여러 탐색 알고리즘 ( 현재 정확히 알고 있는 알고리즘 기준)
- 완전탐색
- 이진탐색 (Binary search)
- 깊이우선탐색 ( Depth-First Search )
- 너비우선탐색 ( Breadth-First Search)
- 해시탐색 (아직 잘 모르는 개념 - 시간이 가장 빠른 것만 알고 있음)
여기까지 보았을 때 탐색 알고리즘에는 각 특징들이 있고 왜? 쓰는지에 대해 대략적으로 해소는 되지만 실제 코딩 문제에 봉착했을 때 DFS를 쓸 지 BFS에 대해서는 판단 기준은 서지 않는다. 일단은 DFS와 BFS에 대해 자세히 알아보자!
2. depth-first search (DFS)
2.1 DFS란?
- 먼저, input으로 들어가게 되는 인접행렬, 인접 리스트와 같은 개념은 생략하였다.
- 백문이 불여일견이다.

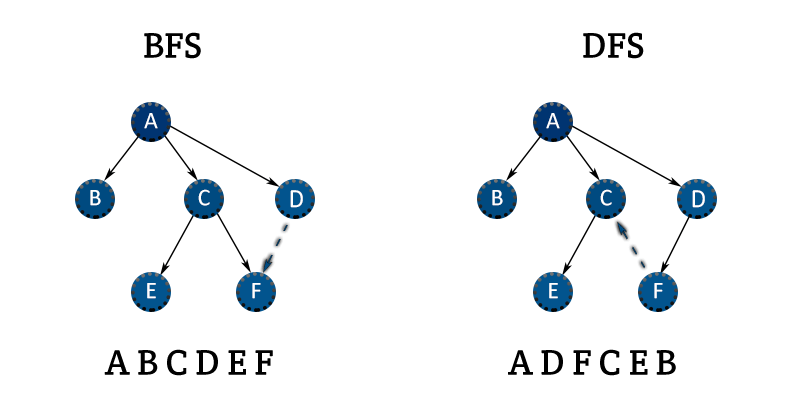
- 왼쪽부터 계층을 모두 거쳐 오른쪽으로 탐색을 진행한다.
- 위의 그림을 보았을 때 깊이 우선 탐색이라는 말이 와닿는다.
- 다시 말하면, 갈 수 있는 만큼 계속해서 탐색하다가 갈 수 없게 되면 다른 방향으로 다시 탐색하는 구조입니다.
- 실행 과정
- 노드를 방문하고 깊이 우선으로 인접한 노드를 방문한다. ( 1 → 2 )
- 또 그 노드를 방문해서 깊이 우선으로 인접한 노드를 방문한다. ( 2 → 3 → 4 )
- 만약 끝에 도달했다면 리턴한다. ( 4 → X )
반복하다가 → 갈 수가 없게 되면 → 탈출 조건
즉, 재귀함수를 이용해서 구현할 수 있음
재귀함수는 stack 특성을 가짐 즉, stack을 이용해 DFS를 구현한다는 것을 의미
재귀함수는 F(n+1) = ? X F(n) 구조를 찾는 것이 중요! (TIL-1 재귀함수 참고)
DFS(node) = node + DFS(node와 인접하지만 방문하지 않은 다른 node)로 생각해 볼 수 있음
2.2 DFS 구현
- 예시 1) 인접 리스트가 주어질 때, 모든 노드를 DFS 순서대로 방문하시오.
2.2.1 인접 리스트 (Adjacent list)
graph = {
1: [2, 5, 9],
2: [1, 3],
3: [2, 4],
4: [3],
5: [1, 6, 8],
6: [5, 7],
7: [6],
8: [5],
9: [1, 10],
10: [9]
}
graph = [[],
[2, 5, 9],
[1, 3],
[2, 4],
[3],
[1, 6, 8],
[5, 7],
[6],
[5],
[1, 10],
[9]]- 인접리스트를 딕셔너리로 표현하느냐, 리스트로 표현하느냐에 따른 표현의 차이 ( 접근하는 슬라이싱만 제대로하면 문제될게 없음)
- 짧지만 코딩 문제 경험상 이중 리스트 구조로 표현하는 것이 괜찮을 것으로 보인다. ( [ [] *len()])과 같은 표현으로 쉽게 구성 가능 )
- graph[i] 에서 i의 의미는 "i에서"라는 시작의 의미이므로 graph[0]은 빈 리스트를 가진다.
- 위의 그림의 예제를 이용한 것이다. 따라서 DFS에 의해 방문 순서를 구하게 되면 [1,2,3,4,5,6,7,8,9,10]이 정답이 된다.
2.2.2 구현을 위한 생각
-
구현 방법
1. 루트 노드부터 시작한다.
2. 현재 방문한 노드를 visted =[] 에 추가한다.
3. 현재 방문한 노드와 인접한 노드 중 방문하지 않은 노드에 방문한다.
4. 2, 3을 반복하며 계층 끝에 도달한다. -
왜 stack을 이용하는지에 대한 생각
stack은 FILO인 선입후출 개념
따라서 처음 시작 노드와 인접한 노드를 모두 저장해두고
가장 왼쪽의 노드의 모든 계층을 탐색한 이후
되돌아와 저장해 둔 노드 중 방문하지 않은 다음 노드로 넘어감
→ 이런 논리는 stack으로 구현하면 알맞음 -
예시를 통한 이해
1과 인접한 (2, 5, 9) 저장
→ 2와 인접한 3
→ 3과 인접한 4
→ 다시 돌아와 1과 인접한 5를 탐색 이후 반복
2.2.3 구현
- 구현 방법에 따른 코드
visited = []
# dictionary의 경우
def dfs_recursion(adjacent_graph, cur_node, visited_array):
visited_array.append(cur_node)
for adjacent_node in adjacent_graph:
if adjacent_node not in visited_array:
dfs_recursion(adjacent_graph, adjacent_node, visited_array)
return
# list의 경우
def dfs_recursion(adjacent_graph, cur_node, visited_array):
visited_array.append(cur_node) # (1)
for adjacent_node in adjacent_graph[cur_node]: # (2)
if adjacent_node not in visited_array: # (2)
dfs_recursion(adjacent_graph,adjacent_node,visited_array) # (3)
return visited_array # (4)
dfs_recursion(graph, 1, visited)
print(visited)(result)
[1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
- (1) : 현재 노드를 visted에 추가
- (2) : 인접 리스트를 통해 추가된 노드와 인접한 노드를 찾은 후, visited에 없는지 확인
- (3) : (1)과(2)는 반복적인 작업이므로 재귀함수를 통해 cur_node만 바꿔줌
- (4) visted_array는 방문 순서를 나타냄
위의 예제는 DFS의 가장 뼈대가 되는 것으로 이해가 중요!
3. Breadth-first search (BFS)
3.1 BFS란?
- 백문이 불여일견

- 같은 계층을 모두 탐색한 이후 다음 계층을 탐색하는 과정을 거침
- 1에 인접한 [2, 3, 4] 노드를 모두 queue에 저장한 이후 가장 처음에 넣은 노드를 꺼내서 탐색을 시작함
- "가장 처음에 넣은 노드"가 의미하는 것이 큐를 이용하여 BFS를 구현할 수 있음
3.2 BFS 구현
3.2.1 인접 리스트
graph = [[],
[2, 3, 4],
[1,5],
[1,6, 7],
[1,8],
[2,9],
[3,10],
[3],
[4],
[5],
[6]]- 이중 리스트로 결과가 [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]이 나올 수 있도록 구성
3.2.2 구현 방법
- 루트 노드를 큐에 넣습니다.
- 현재 큐의 노드를 빼서 visited에 추가한다.
- 현재 방문한 노드와 인접한 노드 중 방문하지 않은 노드를 큐에 추가한다.
- 2와 3을 반복한다.
- queue가 비면 탐색을 종료한다.
3.2.3 구현
- 구현 방법에 따른 코드
from collections import deque
def bfs_queue(adj_graph, start_node):
queue = deque([start_node]) # (1)
visited = [] # (1)
while queue: # (2)
current_node = queue.popleft() #(3)
visited.append(current_node) #(3)
for adj_node in adj_graph[current_node]:
if adj_node not in visited:# (4)
queue.append(adj_node)
return visited- 리스트로 구현할 수 있지만 실제 프로젝트에서 queue를 구현한다고 했을 때 내장된 자료구조인 deque를 이용하는 것이 좋음
- (1) : 시작 노드를 queue에 넣어주고 방문 정보 역할을 하는 visited라는 빈 리스트를 생성한다.
- (2) : queue에 원소가 없을 때 까지 while을 돌린다.
- (3) :
queue.popleft()를 이용해 첫번째 인덱스의 원소를 꺼낸 후 visited에 추가한다. - (4) : current_node와 인접해 있는 노드 중 visited에 있지 않은 노드를 queue에 추가한다.
확실히, 재귀함수를 이용하는 DFS보다 이해하기는 쉬움!