BackToBasics - Data Structure (1)

I took a data structure course in the fall of 2021 and it's been a year since then. Recently, I was told by a co-worker at my internship company, who has been a software developer for about more than 10 years, that it is always the best to make the basics as clear and strong as possible. So I decided to write some posts about the basics - data structure, operating system and computer architecture etc. Each post won't be so long so that I can stay focused to finish posting. Let's start on my first BackToBasics post.

Inductive proof

The very first thing that I ran into was the induction. It is widely explained as dominos.

For a predicate (e.g.$\sum_{i=1}^{k+1} 2^0...2^{n-1} = 2^n - 1$),
1) Set a base case and prove the base case.
2) Show that the predicate holds for n+1 when the predicate holds for n (induction step).

What is data structures?

An efficient way of organizing data for computer.

Why do we need data structures?

With appropriate algorithms, we can have better performances when it comes to solving problems.

Performance, here by, means how fast and small your programs are (and, of course, always must be correct).

How to measure performance?

Usually by theoretical analysis because experimental measurement can differ by many factors, for example, hardware, language, compiler and OS etc.

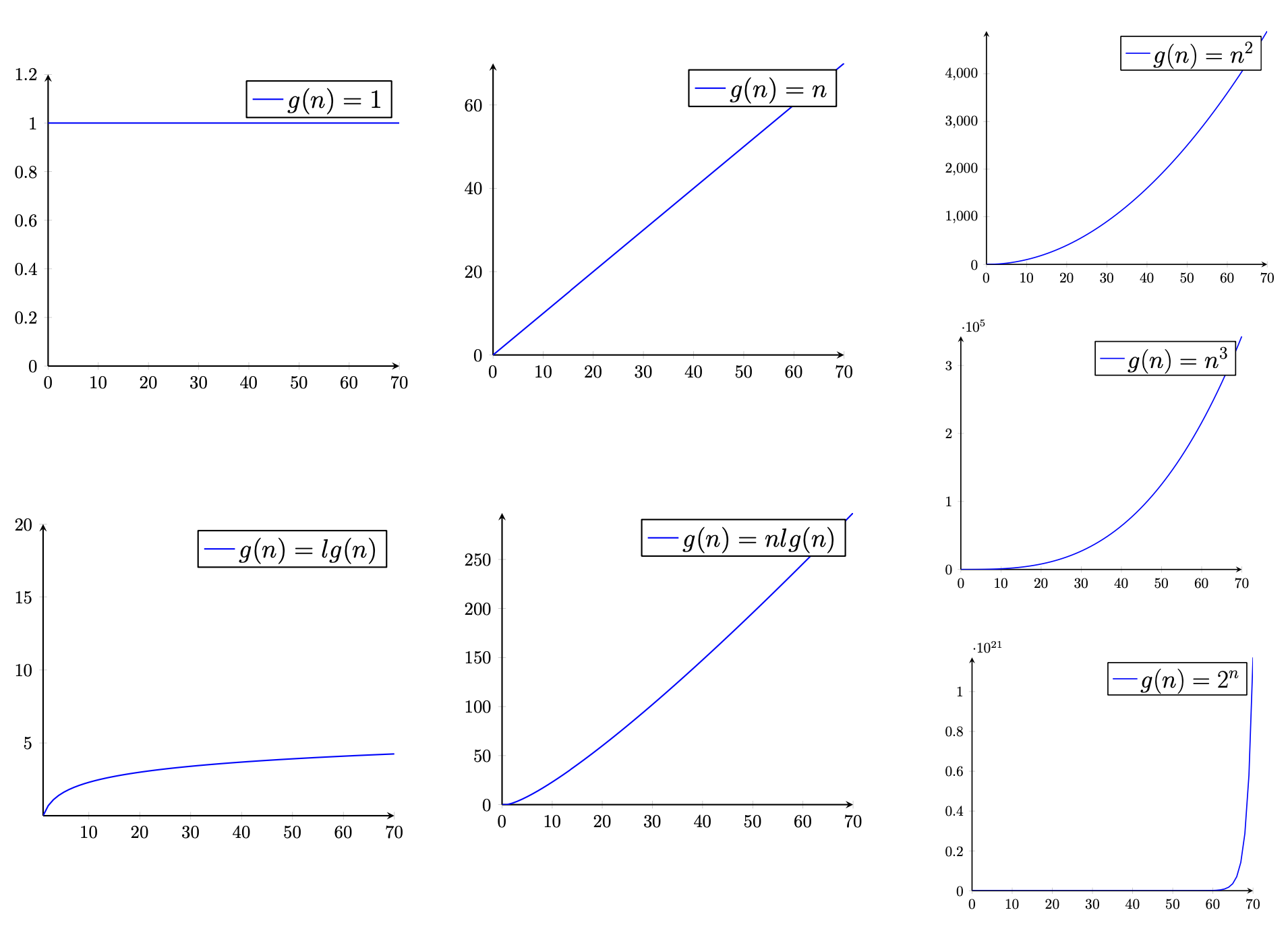
Big-O notation

One of the most popular notation when it comes to measuring performances and denoting time complexity. n means the number of inputs from now on.

1) $O(1)$ : The fastest time complexity. a.k.a constant time complexity, which means the run time is irrelevant to the number of inputs. It does not mean some operation exactly has to be 1 computation.
2) $O(log n)$ : Very efficient. The base of logarithm is always 2 without specific mentions.
3) $O(n)$ : a.k.a linear time complexity.
4) $O(nlogn)$ : The fastest time complexity of sorting algorithms without any additional information.
5) $O(n^2)$ : Quadratic time complexity.
6) $O(n^3)$ : Cubic time complexity.
7) $O(2^n)$ : Exponential time complexity.

Mathematical definition of Big-O notation

Given functions $f(n)$ and $g(n)$,
we say that $f(n)$ is $O(g(n))$ if there are positive constants $c$ and $n_0$ such that

$f(n) ≤ cg(n)$ for $n ≥ n_0$

It simply means that $f(n)$ is bounded by $g(n)$.

Big-Omega

$f(n)$ is $\Omega(n)$ if
$f(n) ≥ cg(n)$ for $n ≥ n_0, c > 0$

Big-Theta

$f(n)$ is $\Theta(n)$ if
$c'g(n) ≤ f(n) ≤ c''g(n)$ for $n ≥ n_0, c' > 0$ and $c'' > 0$