Queue(큐)란?
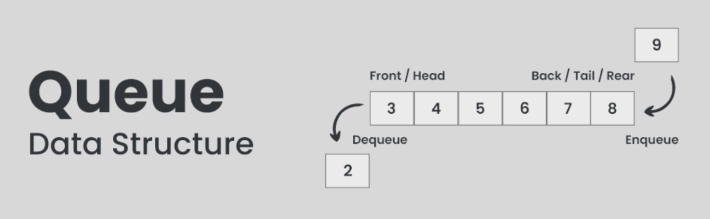
큐(Queue)는 컴퓨터 과학에서 사용되는 데이터 구조 중 하나입니다.
큐는 데이터를 저장하는 추상 자료 구조로, 먼저 들어온 데이터가 먼저 나가는 선입선출(FIFO, First-In-First-Out) 방식으로 동작합니다.

드라이브 스루와 같이
먼저 들어온 차가 먼저 나가는 것을 떠올리면 쉽게 이해할 수 있습니다.
기본 동작:
Enqueue(인큐): 데이터를 큐의 뒤쪽에 추가하는 작업을 의미합니다.
Dequeue(디큐): 큐의 앞쪽에서 데이터를 제거하고 반환하는 작업을 의미합니다.
용도:
프로세스 관리: 작업 대기열을 관리하거나, 시스템 리소스에 대한 접근을 제어할 때 사용됩니다.
네트워크 통신: 데이터 전송이나 메시지 큐에 사용되어 패킷이나 메시지가 도착한 순서대로 처리됩니다.
알고리즘: 너비 우선 탐색(BFS) 등 다양한 알고리즘에서 활용됩니다.
구현:
큐는 배열(Array)이나 연결 리스트(Linked List)로 구현될 수 있습니다. 배열을 사용하면 큐의 크기가 고정되지만, 연결 리스트를 사용하면 크기에 제한이 없습니다.
이러한 큐를 활용한 너비 우선 탐색(BFS)에 대해 알아보겠습니다.
너비 우선 탐색(BFS)란?
너비 우선 탐색(BFS, Breadth-First Search)은 그래프를 탐색하는 알고리즘 중 하나로, 루트 노드로부터 시작하여 인접한 노드를 먼저 모두 탐색한 후, 그 다음 레벨의 노드를 탐색하는 방식입니다. 이는 그래프를 수평적으로 탐색하는 것으로 생각할 수 있습니다.

알고리즘 동작:
- 시작 노드를 큐에 넣습니다.
- 큐가 비어 있지 않은 동안 다음을 반복합니다:
- 큐에서 노드를 하나 꺼냅니다.
- 해당 노드의 이웃한 모든 미방문 노드를 큐에 추가합니다.
- 방문한 노드를 기록합니다.
용도:
최단 경로 탐색: 두 노드 간의 최단 경로를 찾을 때 사용됩니다.
그래프의 연결 여부 확인: 그래프가 연결되어 있는지 확인할 때 유용합니다.
네트워크 트래픽 분석: 네트워크의 특정 지점에 도달하기 위한 경로를 찾을 때 사용됩니다.
구현:
BFS는 주로 큐를 사용하여 구현됩니다. 시작 노드를 큐에 넣고, 큐가 빌 때까지 다음 노드를 꺼내고 그 노드의 이웃을 탐색합니다.
이러한 너비우선탐색을 이용하여
프로그래머스 '가장 먼 노드'라는 문제를 풀어보겠습니다.
가장 먼 노드
n개의 노드가 있는 그래프가 있습니다. 각 노드는 1부터 n까지 번호가 적혀있습니다.
1번 노드에서 가장 멀리 떨어진 노드의 갯수를 구하려고 합니다.
가장 멀리 떨어진 노드란 최단경로로 이동했을 때 간선의 개수가 가장 많은 노드들을 의미합니다.
노드의 개수 n, 간선에 대한 정보가 담긴 2차원 배열 vertex가 매개변수로 주어질 때, 1번 노드로부터 가장 멀리 떨어진 노드가 몇 개인지를 return 하도록 solution 함수를 작성해주세요.
제한사항
- 노드의 개수 n은 2 이상 20,000 이하입니다.
- 간선은 양방향이며 총 1개 이상 50,000개 이하의 간선이 있습니다.
- vertex 배열 각 행 [a, b]는 a번 노드와 b번 노드 사이에 간선이 있다는 의미입니다.
입출력 예
n vertex return
6 [[3, 6], [4, 3], [3, 2], [1, 3], [1, 2], [2, 4], [5, 2]] 3
입출력 예 설명
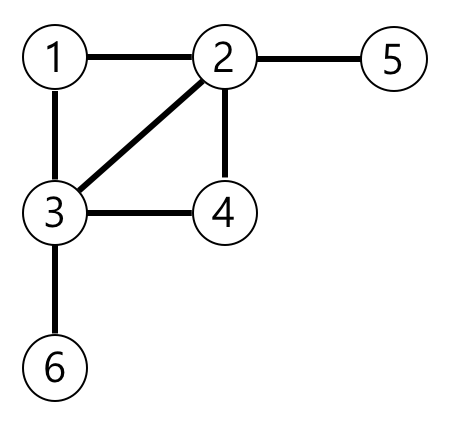
예제의 그래프를 표현하면 아래 그림과 같고, 1번 노드에서 가장 멀리 떨어진 노드는 4,5,6번 노드입니다.
해당 문제는 1번 노드에서
이어진 노드들의 최단거리를 찾아가면서
가장 먼 거리를 가지는 노드들을 찾으면 되겠습니다.
그림으로 이해하면 다음과 같습니다.
- 양방향 그래프이므로 양쪽 모두 기록해준다
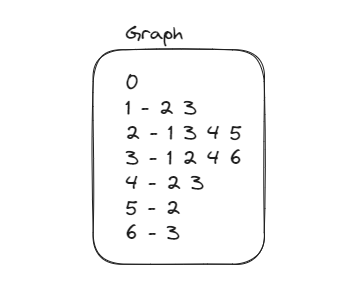
-
출발 노드 + depth(는 0) 을 큐에 넣는다

-
큐에서 노드를 꺼내고 연결된 노드들을 DEPTH와 함께 큐에 넣는다
-
현재 노드를 방문 처리한다.

- 큐가 빌 때까지 3,4 과정을 반복한다
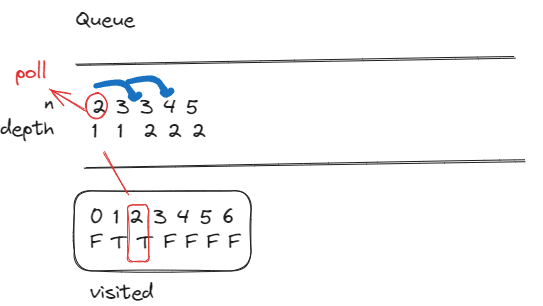
큐와 너비우선탐색을 활용한 코드는 다음과 같습니다.
import java.util.*;
class Solution {
/*
* 각 노드에 연결된 다른 노드들을 리스트로 관리한다. 이것은 양방향 그래프에서 각 노드의 이웃을 저장하는 방법이다.
* 각 엣지에 대해 두 개의 노드 간의 연결을 양쪽으로 기록한다.
* 방문한 노드를 추적하여, 너비 우선 탐색을 수행한다.
*/
// 양방향 그래프를 담을 리스트
ArrayList<ArrayList<Integer>> graph = new ArrayList<>();
public int solution(int n, int[][] edge) {
// 리스트 내 리스트 초기화
for(int i=0; i<=n; i++) graph.add(new ArrayList<>());
// 양방향 그래프이므로 양쪽 모두 기록해준다
for(int[] i: edge) {
int v = i[0];
int w = i[1];
graph.get(v).add(w);
graph.get(w).add(v);
}
// 방문배열 선언 및 초기화
boolean[] visit = new boolean[n+1];
// 그래프, 시작점, 방문배열을 인자로 bfs(너비우선탐색) 진행
return bfs(graph, n, visit);
}
public static int bfs(ArrayList<ArrayList<Integer>> graph, int n, boolean[] visit) {
// 노드 + depth를 함께 들고 다니기 위해 int[]의 Queue 선언
Queue<int[]> queue = new LinkedList<>();
int answer = 0;
int maxDepth = 0;
// 현재 노드(1) + 현재 depth(0)을 큐에 넣는다
queue.offer(new int[] {1, 0});
// 노드 1를 방문 처리한다.
visit[1] = true;
// 큐에 값이 있는 동안 탐색을 계속한다
while(!queue.isEmpty()) {
int[] arr = queue.poll();
int v = arr[0];
int depth = arr[1];
if(maxDepth == depth) answer++; // 최대 길이 노드라면 answer++;
else if(maxDepth < depth) { // 더 긴 거리에 노드가 있다면 answer = 1, maxDepth 갱신
maxDepth = depth;
answer = 1;
}
// v에 대한 ArrayList 순회
for(int i=0; i<graph.get(v).size(); i++) {
int w = graph.get(v).get(i);
// 방문하지 않은 경우 스택에 쌓음 + 방문처리
if(!visit[w]) {
queue.offer(new int[] {w, depth+1});
visit[w] = true;
}
}
}
return answer;
}
public static void main(String[] args) {
Solution sol = new Solution();
int n = 6;
int[][] edge = {{3, 6}, {4, 3}, {3, 2}, {1, 3}, {1, 2}, {2, 4}, {5, 2}};
int result = sol.solution(n, edge);
System.out.println(result);
}
}
풀이 방식은 조금씩 다를 수 있겠습니다.
더 효율적인 코드로 작성 가능하다면 언제든 좋은 피드백 부탁드립니다 :)
이상 큐와 너비우선탐색을 활용한 프로그래머스 - 가장 먼 노드 풀이였습니다.
