Big-O notation
- 알고리즘의 효율성 표기방법 중 하나.
- 시간복잡도: 실행속도. 입력된 N의 크기에 따라 걸리는 시간.
- 공간복잡도: 사용되는 메모리의 양.
- 시간복잡도를 표현할 때 최고차항만 표기.
점근적 표기법(가장 큰 영향을 주는 항만 계산)
- 오메가 표기법 (Big-Ω Notation) : 최상의 실행시간
- 세타 표기법 (Big-θ Notation) : 평균의 실행시간
- 빅오 표기법 (Big-O Notation) : 최악의 실행시간
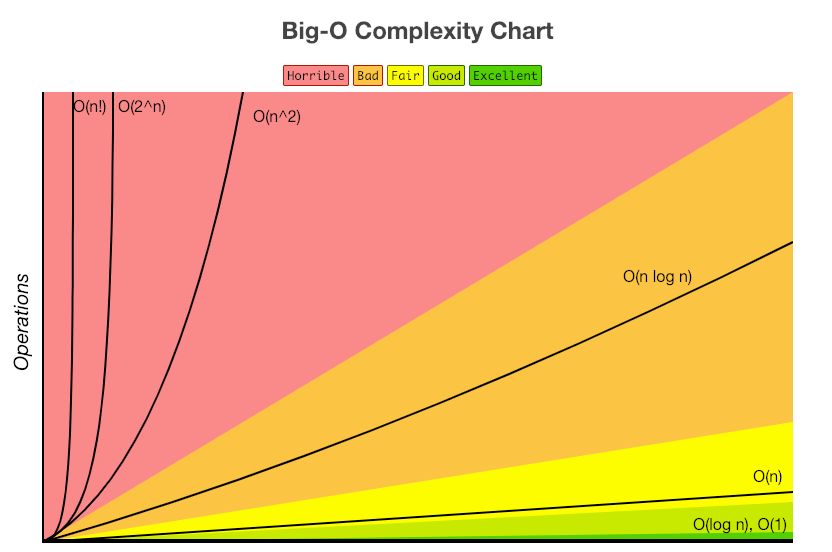
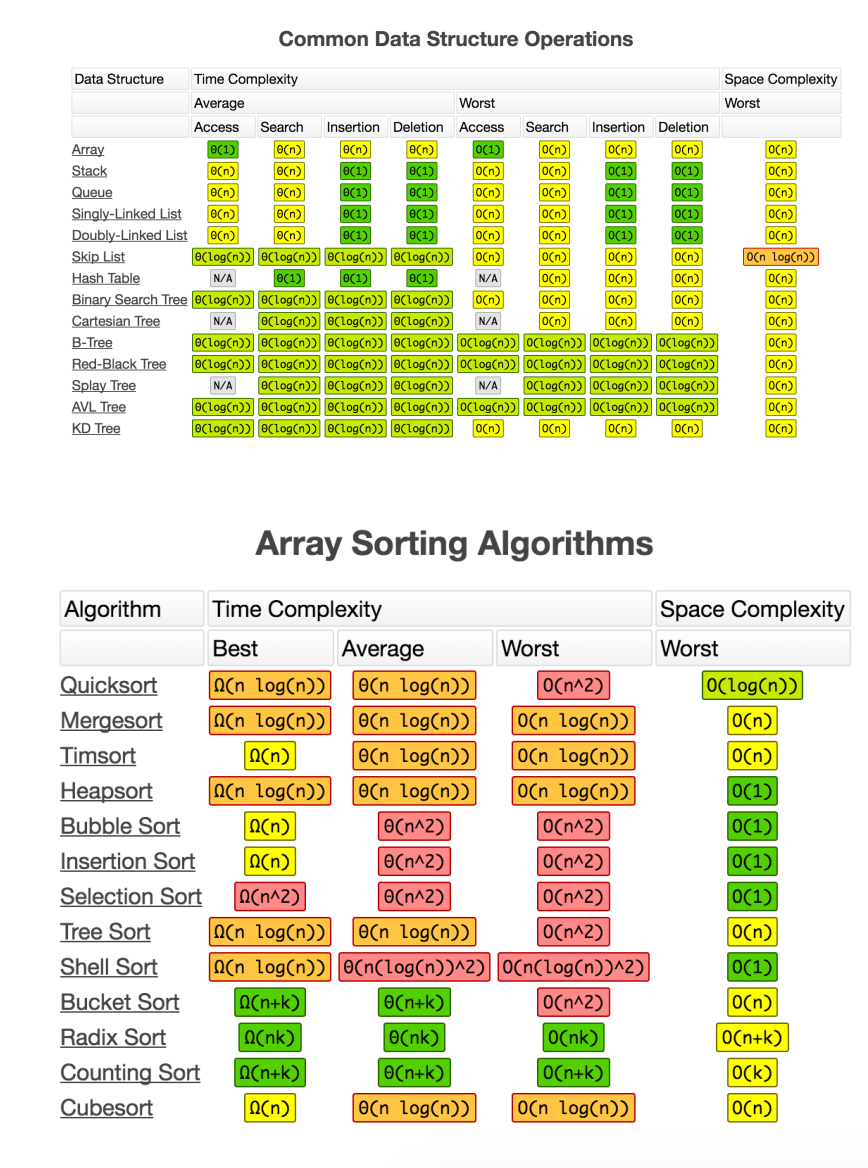
시간복잡도
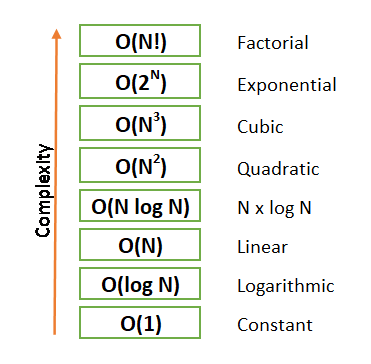
- O(1): 상수(Constant) 시간, 문제 해결 위해 한 단계 실행.
- O(log N): 로그(Logarithmic)시간, 문제 해결위해 필요한 단계들이 특정요인에 의해 줄어듬.
- O(N): 직선적(Linear) 시간, 문제 해결 위해 단계의 수와 입력값 n이 1:1 관계를 가짐.
- O(N log N): 선형로그형, Nlog N, 문제 해결 위해 단계의 수가 N(log2N)번 만큼의 수행시간을 가짐.
- O(N^2): 2차(Quadratic) 시간, 문제 해결 위한 단계의 수는 입력값 N의 제곱
- O(2^N): 지수(Exponential) 시간, 문제 해결 위한 단계의 수는 주어진 상수값 C의 N제곱
| Complexity | 1 | 10 | 100 |
|---|---|---|---|
| O(1) | 1 | 1 | 1 |
| O(log N) | 0 | 2 | 5 |
| O(N) | 1 | 10 | 100 |
| O(N log N) | 0 | 20 | 461 |
| O(N^2) | 1 | 100 | 10000 |
| O(2^N) | 1 | 1024 | 1267650600228229401496703205376 |
| O(N!) | 1 | 3628800 | 표현불가 |
O(1): Constant
입력과 상관없이 복잡도 동일.
def sayHello():
print("hello world")
def sayHi():
print("hello world")
print("hello world")
# 두 method의 복잡도는 똑같음O(N): Linear
입력이 증가하면 시간과 공간 복잡도 또한 선형으로 증가.
def sayHello(n):
for _ in n:
print("hello world")입력 받은 n만큼 반복문 실행.
O(N^2): square
반복문이 두번 있고, 둘 다 n만큼 반복하는 경우.
def sayHello(n):
for x in n:
for y in n:
print(x,y)O(log N)O(N log N)
주어진 입력크기에 따라 처리 시간이 증가하는 정렬 알고리즘에서 많이 사용.
# 이진검색
def binary_search(n, item, first=0, last=None):
if not last:
last = len(n)
midpoint = (last-first)/2+first
if n[midpoint] == item:
return midpoint
elif n[midpoint] > item:
return binary_search(n,item,first,midpoint)
else:
return binary_search(n, item,midpoint,last)시간복잡도 예시
O(1) time
- 배열 인덱스의 원소에 접근 (int a = ARR[5];).
- Linked list에 node 추가.
- Stack에 push/pop 할 때.
- Queue에 insertion/removal 할 때.
- array에 저장된 tree에서 node의 parent 또는 왼/오 child 찾을 때.
- 이중 Linked list에서 다음/이전 요소로 갈 때.
O(n) time
실행 시간이 n의 입력 크기에 비례.
- 하나의 루프를 사용하여 단일 요소 집합을 반복 하는 경우.
- 컬렉션의 절반 이상 을 반복 하는 경우 : O (n / 2) -> O (n).
- 두 개의 다른 루프를 사용하여 두 개의 개별 콜렉션을 반복 할 경우 : O (n + m) -> O (n)
- Palindrome 확인(i.g. eye, madam): 역순으로 읽어도 같음.
- 두 문자열 비교.
- 선형 검색(Linear Search): 순차적으로 검색. linked list에서 자주 쓰임.
- Linked list의 특정 요소 제거할 때(정렬되지않은 상태).
O(log n) time
실행시간이 입력 크기의 log에 비례.
- 이진검색(Binary Search) : 중간값 부터 탐색, tree 구조에서 자주 쓰임.
- 이진 검색 트리에서 최댓값/최소값 찾기.
- 피보나치 수(Fibonacci numbers) 계산 : 피보나치 수는 첫 번째와 두 번째 값이 1이고 다음부터는 그 전의 수와 그전전의 수를 더하는 방식.
O(n log n) time
실행시간이 입력 크기와 입력크기의 log 곱에 비례.
- 컬렉션 정렬을 사용하는 경우 : O(n*log(n)).
- Merge Sort.
- Heap Sort.
- Quick Sort.
O(n^2) time
실행시간이 입력크기의 제곱에 비례.
- 두 개의 중첩 루프를 사용하여 단일 컬렉션을 반복하는 경우 : O (n²).
- 두 개의 중첩 루프를 사용하여 두 개의 다른 콜렉션을 반복 할 경우 : O (n * m) -> O (n²).
- Bubble Sort.
- Insertion Sort.
- Selection Sort.
- 이차원 배열 탐색.
O(n!) time
-
모든 순열 생성.
Ref: