적의 적

풀이

나는 이 문제를 DFS로 접근했다.

1. 처음에 0으로 초기화된 visited 배열을 설정한다.
2. 입력으로 적대관계(a, b)가 주어지는데
   2.1. if 방문하지 않았다면(visited[a]==0 || visited[b]==0), -> visited[a]와 visited[b] 배열의 값이 서로 반대 부호(1, -1)가 되도록 설정
   2.2. if 방문했었다면(visited[a] !=0 && visited[b] != 0), -> visited[a]와 visited[b]가 서로 반대 부호인지 확인

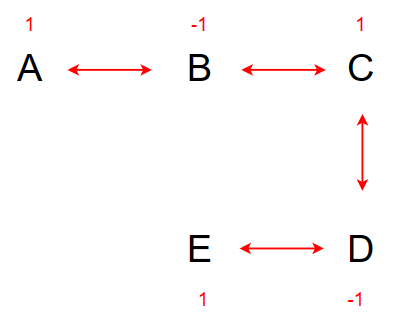
A와 적대 관계인 B가 있고, B와 적대 관계인 C가 있을 때 A와 C는 우호 관계에 있다 -> A와 C는 서로 같은 부호
C와 적대 관계인 D가 있다면, A 역시 D와 적대관계다. -> A와 D는 서로 반대 부호
D와 적대관계인 E가 있다면 E는 A, C와 우호 관계가 된다. -> E는 A, C와 서로 같은 부호
같은 맥락으로, B와 D 역시 우호 관계가 된다. -> B와 D는 서로 같은 부호

시간 복잡도 : O(N+M)

Java

import java.io.*;
import java.util.ArrayList;
import java.util.List;
import java.util.StringTokenizer;

public class Main {

    static List<List<Integer>> graph;
    static int[] visited;

    static int flag = 1;
    public static void DFS(int a, int value){
        if(flag == 0){
            return;
        }
        else {
            visited[a] = value;
            for (int tem : graph.get(a)) {
                if (visited[tem] == 0) {
                    visited[tem] = value * -1;
                    DFS(tem, value*-1);
                } else if (visited[tem] == value) {
                    flag = 0;
                    return;
                }
            }
        }
    }

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));

        StringTokenizer st = new StringTokenizer(br.readLine());
        int N = Integer.parseInt(st.nextToken());
        int M = Integer.parseInt(st.nextToken());

        graph = new ArrayList<>();
        for(int i=0; i<N+1; i++){
            graph.add(new ArrayList<>());
        }

        for(int i=0; i<M; i++){
            st = new StringTokenizer(br.readLine());
            int A = Integer.parseInt(st.nextToken());
            int B = Integer.parseInt(st.nextToken());
            graph.get(A).add(B);
            graph.get(B).add(A);
        }
        visited = new int[N+1];

        for(int i=1; i<N+1; i++){
            if(visited[i]==0){
                DFS(i, 1);
            }
        }
        bw.write(String.valueOf(flag));

        bw.flush();
        bw.close();
        br.close();
    }
}