오큰수

풀이

 백준 골드 4 난이도인 문제다. 단순하게 이중 for문을 사용해서 문제를 풀면 시간복잡도 O(N^2)으로 시간초과 판정이 나온다. 따라서 어떻게 하면 시간복잡도를 줄일 수 있을까 고민하다가 스택이 떠올랐다. 문제의 핵심 아이디어는 스택에 새로 들어오는 수가 top에 존재하는 수보다 크면 그 수는 오큰수가 된다는 것이다.

 이 문제는 시간복잡도 판정에 유의해야 한다. 나는 처음에 for문 안에 while문을 넣었기 때문에 O(N^2)으로 생각했다. 시간초과 판정이 뜨지 않고 정답 판정이 뜬 이유는 기존의 O(N^2)보다는 스택을 활용했기에 약간의 최적화를 했어서라고 생각했다. 하지만 아래 그림을 보면 알 수 있듯이 한 원소는 최대 두 번(push, pop) 연산만을 수행하므로 결과적으로 총 시간복잡도는 O(2N) ->O(N)을 보장한다.

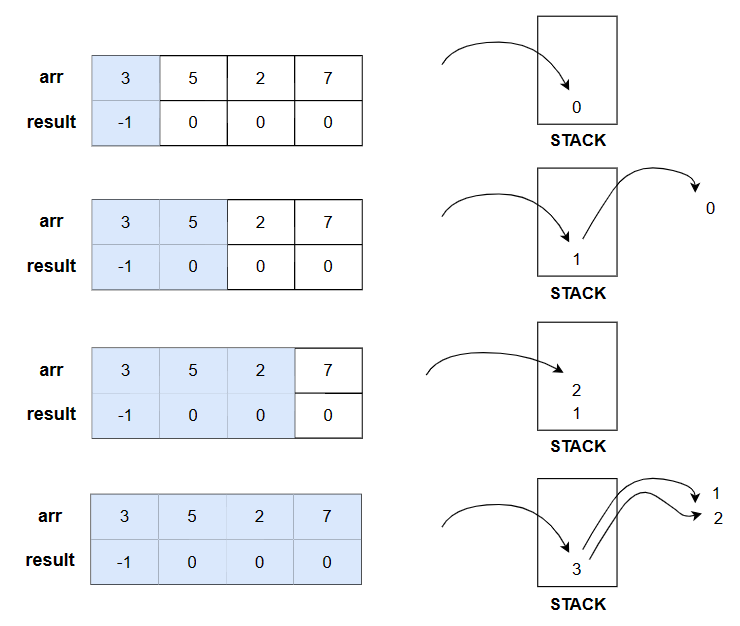
시간 복잡도 : O(N)

Java

import java.io.*;
import java.util.Stack;
import java.util.StringTokenizer;

public class Main {

    public static void main(String[] args) throws IOException {
        // input
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
        int N = Integer.parseInt(br.readLine());
        int[] arr = new int[N];
        int[] result = new int[N];
        Stack<Integer> stack = new Stack<>();
        StringTokenizer st = new StringTokenizer(br.readLine());
        for(int i=0; i<N; i++){
            arr[i] = Integer.parseInt(st.nextToken());
        }

        // code
        for(int i=0; i<N; i++){
            if(stack.isEmpty() || arr[stack.peek()]>=arr[i]){
                stack.push(i);
                result[i] = -1;
            }
            else{
                while (!stack.isEmpty() && arr[stack.peek()]<arr[i]){
                    int tem = stack.pop();
                    result[tem] = arr[i];
                }
                stack.push(i);
                result[i] = -1;
            }
        }

        // output
        for(int i=0; i<N; i++){
            bw.write(String.valueOf(result[i])+" ");
        }
        bw.flush();
        bw.close();
        br.close();
    }
}