순열과 조합을 구할 땐 itertools 모듈의 combinations / permutations도 사용할 수 있지만, 재귀로 풀 수도 있습니다.

백준 문제 4가지를 통해 방법을 소개해 보겠습니다.

순열 구하기

백준 / 실버 3 / 15649. N과 M (1)

• $1$부터 $N$까지 자연수 중에서, 원소 $M$개를 중복 없이, 순서를 고려하여 뽑기
• e.g., $1$부터 $3$까지 자연수 중 $3$개를 고르는 순열은 총 6개
  • $(1, 2, 3)$, $(1, 3, 2)$, $(2, 1, 3)$, $(2, 3, 1)$, $(3, 1, 2)$, $(3, 2, 1)$

어떻게?

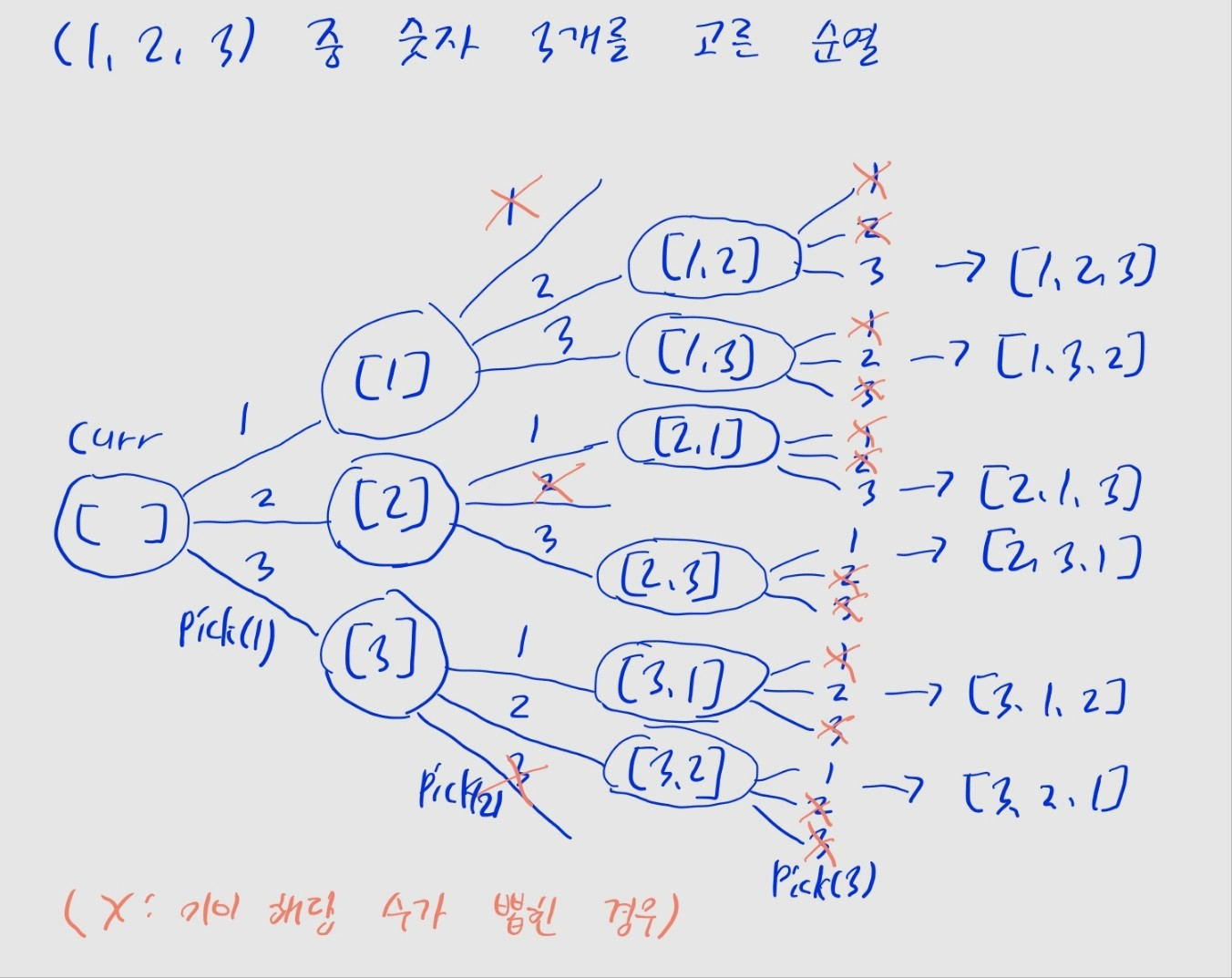
• $1$부터 $N$까지 각 숫자를 순열에 추가하려고 시도합니다.
• 단 해당 숫자가 이미 순열에 뽑힌 경우, 추가하지 않고 다음 숫자를 시도해 봅니다.

풀이

N, M = map(int, input().split())

picked = [False] * (N + 1) 	# 각 숫자를 골랐는지 여부 저장
curr = []					# 순열의 원소를 담은 배열

• 각 숫자가 선택됐는지 여부를 저장하는, $(N + 1)$ 길이의 배열 picked 정의
  • pick[n] -> True: n이 선택됨
  • pick[n] -> False: n이 선택되지 않음
  • 맨 처음엔 순열이 비어 있으므로, 모든 값을 False로 초기화
• 순열의 숫자를 저장할 배열 curr 정의

# 순열의 i번째 숫자 고르기
def pick(i):
	# 모든 숫자를 다 고름
    if i > M:
        for c in curr:
            print(c, end=" ")
        print()
    else:
    	# 순열에 추가할 숫자를 반복문으로 순회
        for k in range(1, N + 1):
            if not picked[k]:		# 순열에 없는 숫자인 경우
                picked[k] = True	# 순열에 추가하기
                curr.append(k)
                pick(i + 1)			# 다음 숫자를 뽑기
                curr.pop()			# 이후 순열에서 빼기
                picked[k] = False
                
pick(1)

• 함수 pick(i) 정의: 순열의 i번째 원소를 선택하는 함수
  • 일단 1번째 원소부터 골라야 하므로 pick(1)부터 호출
• pick() 내부에선 for문을 통해 $1$부터 $N$까지의 수 k를 하나씩 순열에 추가하려고 시도
  • 단, 이미 선택된 수 (picked[k]가 참일 때)의 경우 선택 불가능
• 수 k를 추가할 때, picked 배열의 해당 인덱스 값을 True로 바꿔 주고, curr 배열에 k를 추가
• 이후 pick(i + 1)을 호출하여, 다음 숫자를 선택하기
• 해당 재귀함수 호출이 마무리되면, curr.pop()으로 curr 배열에서 k를 빼고, picked 배열의 해당 인덱스 값을 False로 바꿔야 함
• $i > M$인 경우 완성된 순열 curr을 출력

조합 구하기

백준 / 실버 3 / 15650. N과 M (2)

• $1$부터 $N$까지 자연수 중에서, 원소 $M$개를 중복 없이, 순서 없이 뽑기
• 조합: 주어진 $N$개의 원소들 중 $M$개를 사용하여 만들 수 있는 경우의 수로, 순서를 고려하지 않음
• e.g., $1$부터 $4$까지 자연수 중 $3$개를 고르는 조합은 총 $4$개
  • $(1, 2, 3)$, $(1, 2, 4)$, $(1, 3, 4)$, $(2, 3, 4)$
• 조합 내 숫자는 오름차순이여야 함

어떻게?

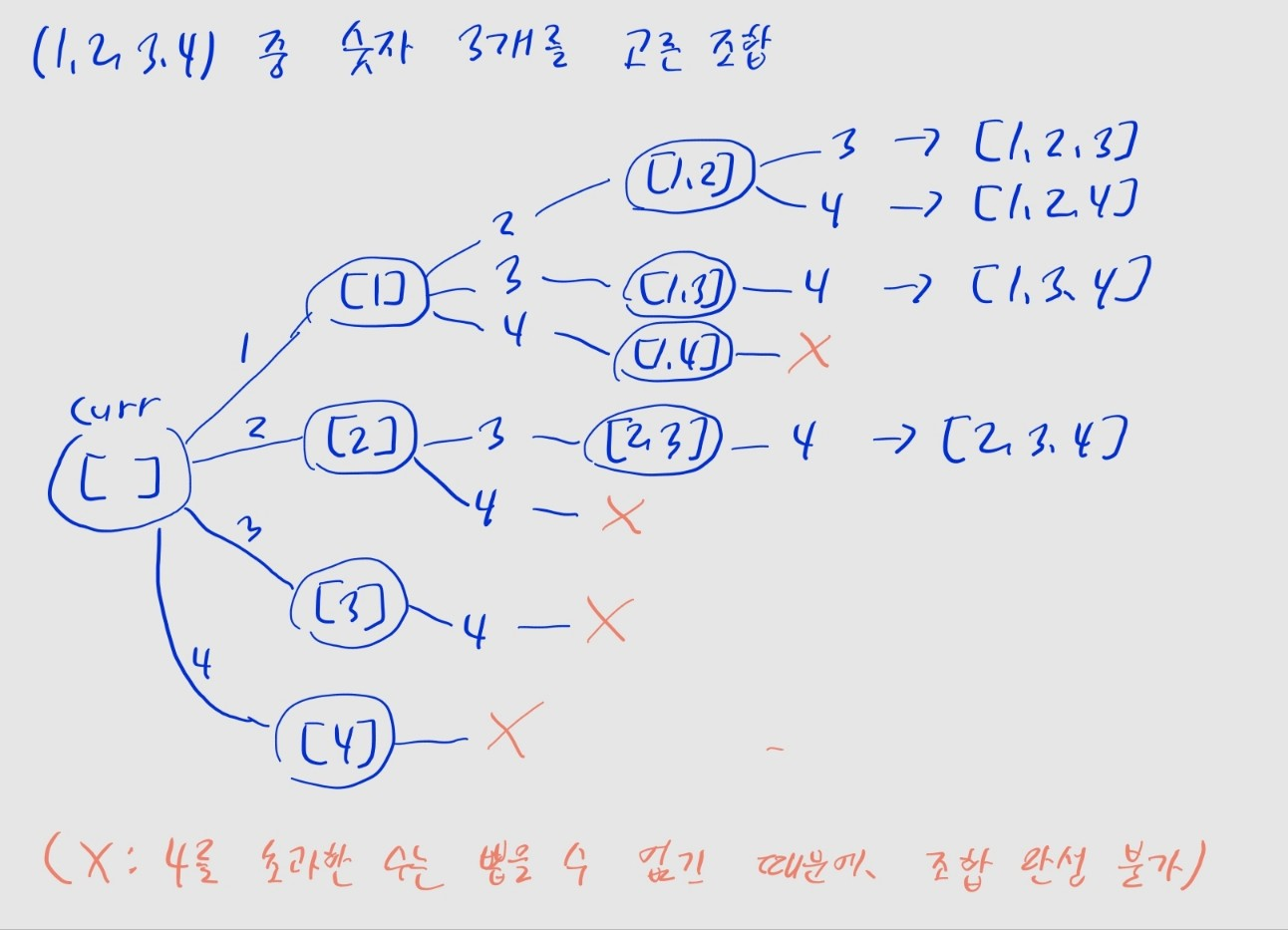
• $1$부터 $N$까지 각 숫자를 조합에 추가하려고 시도합니다.
• 단, 현재 조합에 포함된 수의 최댓값보다 더 큰 수만 추가할 수 있습니다.

풀이

N, M = map(int, input().split())
curr = []

• 순열 내 숫자를 저장할 배열 curr 정의
• 이번엔 picked는 굳이 필요없음: 그 이유는 이후 코드에 설명

def pick(i, begin):
    # 모든 숫자를 다 고름
    if i > M:
        for c in curr:
            print(c, end=" ")
        print()
    else:
    	# 조합에 추가할 수를 반복문으로 순회
        for k in range(begin, N + 1):
            curr.append(k)		# 조합에 추가하기
            pick(i + 1, k + 1)	# 다음 수 뽑기: k + 1부터만 뽑을 수 있음
            curr.pop()         	# 이후 조합에서 빼기
pick(1, 1)

• 함수 pick(i, begin) 정의: 조합 i번째 원소를 선택하는 함수
  • 단, begin 이상의 수만 고를 수 있음 (본 문제에선 조합 내 수를 오름차순으로 나열해야 함)
  • 일단 1번째 원소부터 골라야 하고, 1부터 고를 수 있으니 pick(1, 1)부터 호출
• pick() 내부에선 for문을 통해 begin부터 $N$까지의 수 k를 하나씩 조합에 추가하려고 시도
• 수 k를 추가할 때, curr 배열에 k를 추가
• 이후 pick(i + 1, k + 1)을 호출하여, 다음 수를 선택하기
  • 조합 내 수는 오름차순이여야 함: k 미만의 수를 뽑을 수 없음
  • 조합은 중복을 허용하지 않음: 수 k를 뽑을 수 없음 (이거 때문에 순열에 썼던 picked는 여기선 필요 없음)
  • 즉 begin 매개변수는 k+1로 설정
• 해당 재귀함수 호출이 마무리되면, curr.pop()으로 curr 배열에서 k를 빼야 함
• $i > M$인 경우 완성된 조합 curr을 출력

중복순열 구하기

백준 / 실버 3 / 15651. N과 M (3)

• $1$부터 $N$까지 자연수 중에서, 원소 $M$개를 중복을 허용하고, 순서를 고려하여 뽑기
• e.g., $1$부터 $3$까지 자연수 중 중복을 허용해 $2$개를 구하는 순열은 총 $9$개
  • $(1, 1)$, $(1, 2)$, $(1, 3)$, $(2, 1)$, $(2, 2)$, $(2, 3)$, $(3, 1)$, $(3, 2)$, $(3, 3)$

어떻게?

• $1$부터 $N$까지 각 숫자를 순열에 추가하려고 시도합니다.
• 중복을 허용하므로, 각 숫자가 이미 포함됐는지 확인할 필요가 없습니다!

풀이

N, M = map(int, input().split())
curr = []

def pick(i):
    if i > M:
        for c in curr:
            print(c, end=" ")
        print()
    else:
    	# 이미 같은 수가 선택됐는지 확인하지 않아도 됨
        for j in range(1, N + 1):
            curr.append(j)
            pick(i + 1)
            curr.pop()
            
pick(1)

• 순열 풀이와 거의 동일하지만, 중복이 허용되니 picked 배열은 필요없음
• 순열에 수를 더할 때, 이미 선택됐는지 확인하는 절차가 생략됨

중복조합 구하기

백준 / 실버 3 / 15652. N과 M (4)

• $1$부터 $N$까지 자연수 중에서, 원소 $M$개를 중복을 허용하고, 순서 없이 뽑기
• e.g., $1$부터 $3$까지 자연수 중 중복을 허용해 $2$개를 고르는 조합은 총 $6$개
  • $(1, 1)$, $(1, 2)$, $(1, 3)$, $(2, 2)$, $(2, 3)$, $(3, 3)$
• 조합 내 숫자는 오름차순이여야 함

어떻게?

• $1$부터 $N$까지 각 숫자를 조합에 추가하려고 시도합니다.
• 기존 조합에선, 현재 조합의 수 중 최댓값을 초과하는 수만 추가할 수 있었습니다.
• 중복조합에선 중복을 허용하므로, 현재 조합의 수 중 최댓값 이상의 수만 추가할 수 있는 걸로 조건을 바꿉니다.

풀이

N, M = map(int, input().split())
curr = []

def pick(i, begin):
    if i > M:
        for c in curr:
            print(c, end=" ")
        print()
    else:
        for k in range(begin, N + 1):
            curr.append(k)		
            pick(i + 1, k)	    # 동일 값을 허용: k+1가 아닌 k부터 뽑기 허용
            curr.pop()         	
pick(1, 1)

• 조합 풀이와 동일하지만, 동일 값을 뽑는 것을 허용
• 즉 재귀함수 호출 시, begin 자리에 올 값을 k + 1(이번에 뽑은 수 다음 수)에서 k(이번에 뽑은 수)로 수정

기억할 점

이렇게 풀지 마시고 itertools.permuations, itertools.collections 쓰세요....
ㅠㅠㅠㅠㅠ