정규화 란?
- 정규화(Normalization)의 기본 목표는 테이블 간에 중복된 데이터를 허용하지 않는 것이다.
- 데이터의 중복을 최소화하기 위해 여러 개의 관련된 테이블로 데이터를 묶는 것이다.
- 중복된 데이터를 허용하지 않음으로써 무결성(integrity)를 유지할 수 있으며, DB의 저장 공간 효율을 높일 수 있다.
왜 정규화를 해야 할까?
-
정규화를 하지 않으면 테이블에 중복된 데이터가 많아지고 데이터의 삽입, 삭제, 수정 등을 하기 어려워진다. 이를 이상현상(anomaly)이라고 한다.
-
이러한 이상현상을 제거하기 위해서 정규화가 필요하다.
-
예를 들어 고객 테이블에 다음과 같은 컬럼이 있다고 가정하면
고객번호 | 고객명 | 전화번호 | 등급 | 할인율 -
삽입 이상: 테이블에 새로운 레코드를 삽입할 때, 필요한 컬럼의 값이 없어서 레코드를 삽입하지 못하는 경우를 말한다.
- 기존 테이블의 등급 컬럼에는 VIP(10%), GOLD(7%), SILVER(5%)의 세가지 등급이 있고 등급에 따라 할인율이 결정되는 상황을 가정해보자.
- 이런 상황에서 고객 테이블에 새로운 NEW 등급과 할인율 3%를 적용하고 싶은 경우 NEW 등급의 고객 정보가 없어 테이블에 추가할 수 없다.
- 즉, 신규회원을 위한 등급을 새로 만들려고 하지만 등록할 신규회원이 전혀 없는 상태에선 새로운 등급 자체를 만들 수 없다는 것이다.
-
삭제 이상: 데이터의 삭제 시 의도하지 않았던 전혀 다른 데이터가 삭제되는 현상을 말한다.
- 예를 들어 등급이 NEW인 고객이 단 한 명 있을 때 이 고객을 삭제해버리면 NEW 등급과 NEW 등급의 할인율 정보도 삭제되어버린다.
-
수정 이상: 하나의 테이블이 불필요한 중복 레코드들을 포함하여 데이터베이스의 일관성이 훼손되는걸 말한다.
- 만약 VIP 등급의 할인율을 10%에서 8%로 하향하는 수정 작업을 해야 한다면 고객 테이블의 모든 데이터를 수정해야 한다. 이러한 수정 작업은 고객 테이블에 레코드의 개수가 많을 수록 더 많은 시간이 필요하다.
- 만약 수정 작업 중간에 오류가 발생한다면, 같은 VIP 등급 고객들간에 적용되는 할인율이 달라질 수 있다. 이는 데이터의 일관성이 훼손된 것이다.
-
이상 현상 외에도 다음과 같은 목적이 있다.
- 어떠한 릴레이션이라도 데이터베이스 내에서 표현할 수 있도록 만든다.
- 좀 더 간단한 관계 연산에 기초하여 검색 알고리즘을 효과적으로 만든다.
- 새로운 형태의 데이터가 삽입될 때 릴레이션을 재구성할 필요성을 줄인다.
함수적 종속성(functional dependency)
- 함수적 종속성이란 속성들 간의 값의 연관관계를 표현한 것으로, 특정 시점의 릴레이션 인스턴스를 분석하여 파악할 수 있다.
| 고객번호 | 고객명 | 전화번호 | 등급 | 할인율 |
|---|---|---|---|---|
| c1 | 홍길동 | 010-1234-5678 | GOLD | 5% |
| c2 | 김철수 | 010-4567-1234 | VIP | 10% |
| c3 | 이영희 | 010-8794-5651 | NEW | 3% |
| c4 | 윤봉길 | 010-5443-5678 | GOLD | 5% |
| c5 | 안창호 | 010-3633-5678 | VIP | 10% |
| c6 | 김구 | 010-6766-5678 | NEW | 3% |
- 위 테이블을 보면 고객의 등급에 따라 할인율이 결정된다.
- 이러한 두 속성에 대한 연관성을 함수적 종속이라고 하며 아래와 같이 표기한다.
{등급} -> {할인율} - 좌측의 속성을 결정자(determinant)라고 하며 우측의 속성을 종속자(dependency)라고 한다.
- 함수적 종속성의 형식적 정의는 다음과 같다.
임의의 릴레이션 스키마 R의 인스턴스에 포함되는 서로 다른 두 레코드 r1, r2와 속성(컬럼)집합 X와 Y에 대해, r1[X]=r2[X]일 때, r1[Y]=r2[Y]이면 함수적 종속성 X -> Y가 성립한다. - 위 테이블과 같이 함수적 종속성이 예외없이 성립하면 적법한 릴레이션(legal relation)이라 하고 예외가 있다면 적법하지 않은 릴레이션(illegal relation)이라 한다.
- 함수적 종속성을 검사하면 어느 속성에 의해 중복되는 데이터가 발생하는지 알 수 있다. 위 테이블에선 10%, 5%, 3% 라는 데이터가 두 번씩 중복되는 것을 알 수 있다.
함수적 종속성의 추론 규칙과 카노니컬 커버
- 함수적 종속성은 데이터의 중복과 갱신 이상 현상을 제거하는 작업에 있어 중요한 판단 기준이 되므로 테이블 내에 존재하는 모든 함수적 종속성을 추출하는 것이 매우 중요하다.
- 하지만 테이블의 크기가 방대하거나 3개 이상의 속성이 함수적 종속성에 연관될 경우 함수적 종속성 여부를 진단하기 어렵다.
- 이를 위해 함수적 종속성 집합을 논리적으로 확장하여 찾아내지 못한 종속성을 모두 찾기 위한 추론 규직을 적용할 수 있다.
- 함수적 종속성 추론 규칙은 다음과 같다.
- 재귀성 규칙 : Y가 X의 부분 집합이면 X → Y 이다. (Y ⊆ X이면, X→Y이다.)
- 부가성 규칙 : X → Y 이면 XZ → YZ 이다.
- 이행성 규칙 : X → Y 이고 Y → Z 이면 X → Z 이다.
- 분해 규칙 : X → YZ 이면 X → Y 이다.
- 합집합 규칙 : X → Y 이고 X → Z 이면, X → YZ 이다.
- 의사 이행성 규칙 : X → Y 이고 WY → Z 이면, WX → Z 이다.
- 규칙 1, 2, 3은 암스트롱의 추론 규칙이라고 한다.
- 규칙 4, 5, 6은 암스트롱의 추론 규칙으로부터 유도된 규칙이다.
- 고객 테이블에서 함수적 종속성
{고객번호} → {고객명}과{고객명} → {전화번호}가 성립하면 추론 규칙을 통해{고객번호} → {전화번호}도 성립한다는 걸 유추할 수 있다. - 이렇게 명시적으로 주어진 함수적 종속성과 그로부터 추론될 수 잇는 모든 종속성 집합을 F의 클로저(closure)라고 부르고
F+로 표기한다. - 함수적 종속성 추론 규칙을 통해 모든 함수적 종속을 찾아내어 클로저를 유도했다 하더라도 클로저에는 자명한 종속성(예를 들어 A → A 등)과 중복된 종속성(A → BC와 A → B, A → C 등)이 포함된다.
- 이러한 불필요한 함수적 종속성을 제거하려면 종속 정보에 대한 손실 없이 간소화된 함수적 종속성 집합인
카노니컬 커버(canoical cover)를 구해야 한다. - 카노니컬 커버의 커버(cover)란?
주어진 함수적 종속성 집합 E에 대해 E가 함수적 종속성 집합F+(F의 클로저)에 포함되면 E의 모든 함수적 종속성들이 F로부터 추론될 수 있으며, 이때 F가 E를 커버한다고 표현한다. - F의 카노니컬 커버는
F+에 존재하는 모든 함수적 종속성을 커버할 수 있는 최소한의 함수적 종속성들로만 이루어진 집합이다.
정규형(Normal Form)
- 정규형은 특정 갱신 이상 현상이 제거된 릴레이션의 형식이다.
- 순서에 따라 규칙이 누적되므로 상위 정규형은 하위 정규형의 조건을 모두 만족해야 한다.
예를들어 제3정규형은 제1정규형과 제2정규형의 조건을 모두 만족해야 한다. - 그러나 일부 특수한 경우에는 누적조건을 만족하지 못할 수도 있다.
- 대부분의 경우 정규화는 제3정규형이나 보이스-코드 정규형까지만 진행하며 그 이상의 정규형이 필요한 상황은 드물다.
- 또한 정규화를 많이 할수록 조인(JOIN) 연산이 증가하므로 그에 대한 비용이 늘어날 수 있다.
- 하지만 그러한 비용보다 편익이 크다면, 그 이상의 정규형을 적용하는걸 고려할 수 있다.
정규형의 단계와 그 방법
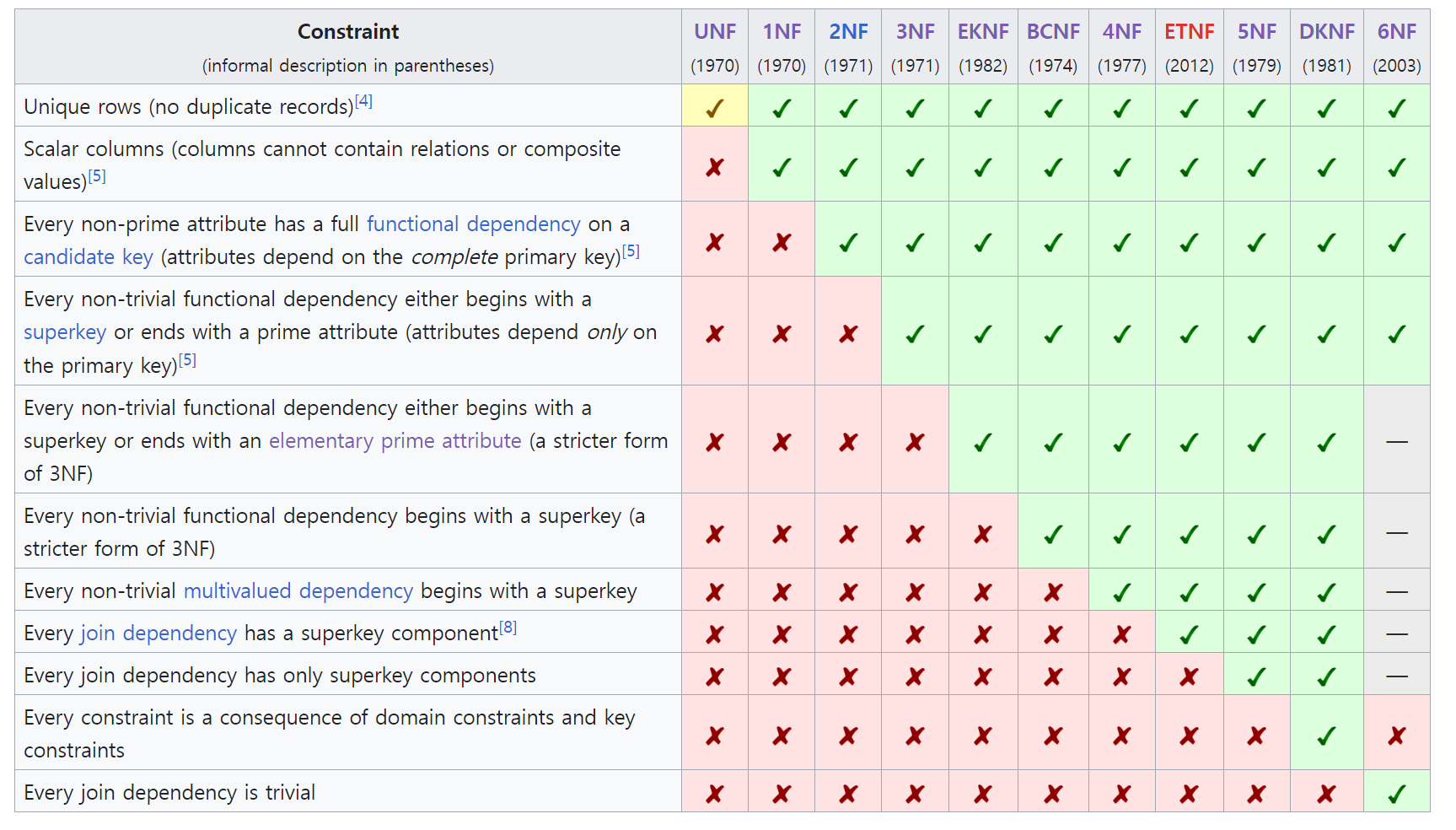
비정규형(Unnormalized form, UNF): 아직 정규화 되지 않은 상태를 말한다. 어떤 정규형의 조건도 만족하지 않는다.제1정규형(1NF): 각 열(속성)은 원자적인 값만을 가져야 되고 각 행은 유일한 식별자(Primary Key)를 가져야 한다.제2정규형(2NF): 제1정규형에서 부분적 함수 종속 제거제3정규형(3NF): 제2정규형에서 이행적 함수 종속 제거기본 키 정규형(Elementary key normal form, EKNF): 제3정규형을 약간 개선한 것보이스-코드 정규형(BCNF): 제3정규형에서 결정자이면서 후보키가 아닌 것 제거제4정규형(4NF): 보이스-코드 정규형에서 다중값 종속성 제거ETNF(Essential tuple normal form): 모든 조인 종속성에 슈퍼키 구성 요소가 있음제5정규형(5NF 또는 PJNF(projection–join normal form)): 모든 조인 종속성에는 수퍼키 구성 요소만 있음도메인-키 정규형(Domain-key normal form, DKNF): 도메인 제약 조건 및 키 제약 조건 이외의 제약 조건이 없음제6정규형(6NF): 사소한 조인 종속성만 충족
1NF: 모든 속성은 원자적인 값만을 가지고 각 행은 식별자를 가짐
- 모든 속성에 반복 그룹이 존재하면 안되고 원자적인 값 만을 가져야 된다.
- 모든 행은 식별자로 완전하게 구분되어야 한다.
- 한 릴레이션 안에 내포된 릴레이션이 없어야 한다.
- DB의 모든 테이블은 적어도 제1정규형 조건을 만족해야 한다.
- 각 행의 데이터에 (사과, 포도) 같은 식으로 여러개의 데이터가 들어가면 안된다.
- 한 컬럼의 모든 데이터는 같은 자료형이어야한다. 예를 들면 어떤 값은 숫자 자료형인데 어떤 값은 문자 자료형이면 안된다
- 모든 컬럼은 고유한 이름을 가져야 한다.
- 데이터가 저장된 순서는 중요하지 않다.
2NF: 1NF에서 부분적 함수 종속 제거
- 1NF 테이블의 모든 비기본 속성(non-prime attribute, 후보 키에 속하지 않은 속성)들이 후보 키에 속한 속성들 전체에 함수 종속됐다면 이 테이블은
2NF이다. - 다시 말하면 기본키가 아닌 모든 속성들이 기본키에 완전 함수 종속되야 한다는 것이다.
- 다음과 같은 시험점수 테이블이 있다.
점수id | 학생번호 | 과목번호 | 점수 | 교수 - 교수는 기본키(PK)인 학생번호와 과목번호가 아니라 과목번호에만 종속돼있다.
- 따라서 과목 테이블을 따로 만들고 거기에 교수 컬럼을 넣거나 과목과 교수 테이블을 각각 따로 만들어주는 방식으로 위 테이블을 분해하면 2NF를 충족할 수 있다.
점수id | 학생번호 | 과목번호 | 점수
과목번호 | 과목명 | 교수
3NF: 2NF에서 이행적 함수 종속 제거
- 2NF 테이블 내의 모든 속성이 기본 키에만 의존하며, 다른 후보 키에 의존하지 않으면
3NF가 된다. X → Y이고Y → Z이면X → Z이다. 여기서 Z는 X에 이행적으로 함수 종속(transitive dependency)되어있다고 한다.- 다음과 같은 테이블이 있다.
고객번호 | 등급 | 할인율 - 기본키는 고객번호이고 등급은 기본키가 아니지만 할인율은 등급에 종속되어 있다.
- 위 테이블을 고객번호별 등급과 등급별 할인율을 나타내는 테이블로 분해하면 3NF를 충족할 수 있다.
고객번호 | 등급
등급 | 할인율
보이스-코드 정규형(BCNF): 3NF에서 결정자이면서 후보키가 아닌 것 제거
- 3NF에서 모든 결정자가 후보키가 되도록 만든 것이
BCNF이다. - 다음과 같은 수강 테이블이 있다.
학번 | 과목 | 강사 - 요구사항은 다음과 같다.
- 학생은 여러 개의 과목을 수강할 수 있지만 같은 과목명을 여러 개 수강하지 못한다.
- 각 강사는 하나의 과목만 담당한다.
- 여기서
{학번, 과목} → 강사이고강사 → 과목이다. 하지만 강사는 후보키가 아니다. - 그러므로 다음과 같이 테이블을 분해하면 BCNF를 충족할 수 있다.
학번 | 강사
강사 | 과목
제4정규형(4NF): BCNF에서 다중값 종속성 제거
- BCNF 테이블에서 다중값 종속성(multi-valued dependency)을 제거한 테이블이
4NF이다. - 테이블에 컬럼이 최소 3개 이상이어야 다중값 종속성이 생길 수 있다.
- 테이블에
A | B | C3개의 컬럼이 있고, 하나의 A값이 B의 여러 값에 영향을 미치면서, B와 C컬럼이 서로 독립적이면, 다중값 종속성이 있다고 할 수 있다. - 예를 들면 다음과 같은 학생 테이블이 있다.
학번 | 과목 | 취미 - 한 학생이 여러 개의 과목을 수강할 수 있고 과목과 취미가 서로 상관이 없다면 이 테이블은 다중값 종속성이 있다고 볼 수 있다.
- 따라서 다음과 같이 테이블을 분해하면 4NF를 충족할 수 있다.
학번 | 과목
학번 | 취미
제5정규형(5NF 또는 PJNF): 모든 조인 종속성에는 수퍼키 구성 요소만 있음
- 4NF 테이블에서 조인 종속성(join dependency)를 제거한 테이블이
5NF이다. - 조인 종속성이란 한 테이블을 분해한 테이블들을 다시 서로 조인했을 때 원래의 테이블과 동일하게 복원되는 것을 말한다.
- 예를 들면 다음과 같은 4NF 테이블과 조건이 있다.
판매자 | 제품 | 고객 - 판매자는 제품을 여러 고객에게 판매할 수 있다.
- 고객은 판매자의 여러 제품을 구매할 수 있다.
- 제품은 고객에게 사용되는데, 같은 제품도 여러 판매자가 있을 수 있다.
- 다음과 같이 테이블을 3개로 분해하면 5NF를 충족할 수 있다.
판매자 | 제품
판매자 | 고객
고객 | 제품
도메인-키 정규형(DKNF): 도메인 제약 조건 및 키 제약 조건 이외의 제약 조건이 없어야 함
- 5NF 테이블에서 도메인 제약 조건 및 키 제약 조건 이외의 제약 조건이 제거된 테이블이
DKNF이다. - 도메인 제약 조건은 지정된 특성에 대해 허용되는 값을 정의하는 제약조건이다.
- 키 제약 조건은 지정된 테이블에서 행을 고유하게 식별하는 특성을 정의하는 제약조건이다.
- 3NF, BCNF, 4NF, 5NF는 모두 도메인-키 정규형의 특수한 사례이다.
- 예를 들면 다음과 같은 부자 목록 테이블과 조건이 있다.
| 부자 이름 | 부자 등급 | 달러 순자산 |
|---|---|---|
| Steve | 백만장자 | 124,543,621 |
| Roderick | 억만장자 | 6,553,228,893 |
| Katrina | 억만장자 | 8,829,462,998 |
| Gary | 백만장자 | 495,565,211 |
- 부자 도메인은 사전 정의된 부자 샘플의 모든 부자 이름으로 구성되어 있다.
- 부자 등급 도메인은 '백만장자'와 '억만장자' 값으로 구성되어 있다.
- 순자산 도메인은 1,000,000 이상의 모든 정수로 구성되어 있다고 가정한다.
- 부자 등급과 달러 순자산을 연결하는 제약조건이 있다.
- 백만장자는 1,000,000에서 999,999,999의 달러 순자산을 갖고, 억만장자는 1,000,000,000또는 그 이상의 달러 순자산을 가진다.
- 이러한 제약 조건은 도메인 제약 조건도 아니고 키 제약 조건도 아니다.
- 이 제약조건을 테이블에서 제거함으로써 일관성 없는 데이터가 삽입되는 문제를 예방할 수 있다.
- 예를 들면 달러 순자산이 1,500,000,000인데 백만장자 등급으로 데이터가 삽입되면 데이터의 일관성이 없어진다.
- 위 테이블에서 부자 등급 컬럼을 다음과 같이 분해하면 DKNF를 충족할 수 있다.
- 부자 목록 테이블
| 부자 이름 | 달러 순자산 |
|---|---|
| Steve | 124,543,621 |
| Roderick | 6,553,228,893 |
| Katrina | 8,829,462,998 |
| Gary | 495,565,211 |
- 달러 순자산 범위에 대한 부자 등급 테이블
| 부자 등급 | 최소 | 최대 |
|---|---|---|
| 백만장자 | 1,000,000 | 999,999,999 |
| 억만장자 | 1,000,000,000 | 999,999,999,999 |
- 백만장자 또는 억만장자의 지위는 부자 등급 테이블에 정의된 달러 순자산에 의해 결정되므로 정규화 후에도 유용한 정보가 손실되지 않는다.
역정규화(Denormalization)
- 정규화의 반대 과정으로 정규화를 통해 분리되었던 릴레이션을 다시 통합하는 것이다.
- 정규화되지 않은 스키마와 역정규화 스키마는 전혀 다른 것이다.
- 역정규화를 효율적으로 하기 위해선 우선 스키마가 정규화되어 있어야 한다.
- 역정규화는 정보의 부분적 중복을 허용하지만 데이터 접근 성능을 개선하는 기법이다.
- 정규화를 많이 진행할 수록 하나의 릴레이션이 여러 개의 릴레이션으로 분리되므로 조인 연산이 증가한다.
- 일반적으로 조인이 증가할 수록 데이터를 조회하는 쿼리의 실행속도는 느려진다.
- 따라서 정규화에 따른 성능 문제를 개선하기 위해 역정규화를 고려할 수 있다.
- 단 역정규화를 하면 데이터의 중복이 늘어나므로 데이터의 삽입, 삭제, 갱신 속도는 느려질 수도 있다.