SymPy는 컴퓨터 대수 프로그램(CAS)을 지원하는 Python 라이브러리입니다. SymPy의 내장 기능을 사용하여 벡터 미적분학 문제를 쉽게 해결하고, 시각화할 수 있습니다.
from sympy import * # SymPy의 기본적인 함수들입니다.
from sympy.vector import * # 벡터 관련 기능을 사용할 수 있습니다.
import numpy as np # SymPy의 계산 결과를 수치 해석적으로 분석할 수 있습니다.
import plotly.express as px # 시각화를 위한 라이브러리입니다.
import plotly.graph_objects as go
import plotly.figure_factory as ff가독성을 위해서, 몇 가지 변수들의 LaTeX 형식을 조정할 필요가 있습니다. 단위 벡터(unit vector)는 , , 를 사용합니다.
N = CoordSys3D('N')
x, y, z = N.x, N.y, N.z # 변수로 사용할 x, y, z
x._latex_form = 'x'
y._latex_form = 'y'
z._latex_form = 'z'
i, j, k = N.i, N.j, N.k # 단위 벡터로 사용할 i, j, k
i._latex_form = '\mathbf{\hat i}'
j._latex_form = '\mathbf{\hat j}'
k._latex_form = '\mathbf{\hat k}'벡터장(vector field)
벡터장 를 정의해봅시다.
F = -y * i + x * j
F[출력 결과]
, 에 값을 대입하여 해당 좌표에서의 벡터를 구할 수 있습니다.
for pt in ((1, 0), (2, 2), (3, 0), (0, 1), (-2, 2),):
print(pt, F.subs({x: pt[0], y: pt[1]}), sep=': ')[출력 결과]
(1, 0): N.j
(2, 2): (-2)*N.i + 2*N.j
(3, 0): 3*N.j
(0, 1): (-1)*N.i
(-2, 2): (-2)*N.i + (-2)*N.j벡터장을 그릴 수도 있습니다! NumPy와 Plotly를 사용하여 벡터장을 그려봅시다.
# F를 lambdify(NumPy에서 사용할 수 있게 함)합니다.
vars = symbols('x y')
F_func = F.subs({key: value for key, value in zip((x, y,), vars)}) # 기존 N.x, N.j는 lambdify를 지원하지 않기 때문에 변수 변경
x_func = lambdify(vars, F_func.coeff(i), modules='numpy')
y_func = lambdify(vars, F_func.coeff(j), modules='numpy')
# [-5, 5]x[-5, 5]에서 벡터장을 그립니다.
xy = np.meshgrid(np.linspace(-5, 5, 11), np.linspace(-5, 5, 11))
xx = xy[0].flatten() # 모두 flatten하여 1D array로 만듭니다.
yy = xy[1].flatten()
uu = x_func(*xy).flatten()
vv = y_func(*xy).flatten()
fig = ff.create_quiver(xx, yy, uu, vv) # Quiver (화살표 그래프)를 그립니다.
fig.update_yaxes( # 비율(aspect-ratio)를 1로 조정합니다.
scaleanchor='x',
scaleratio=1,
)
fig.show()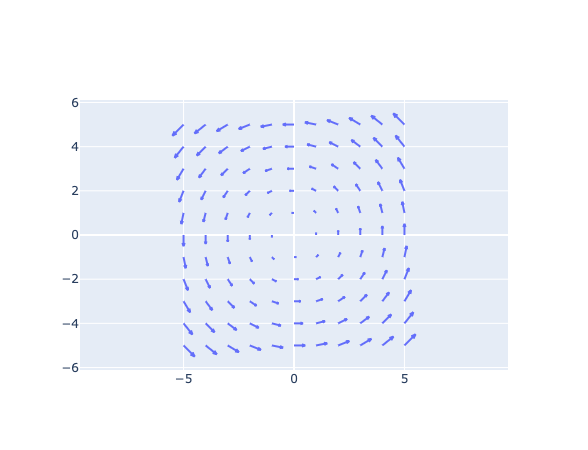
이를 간단히 함수화할 수 있습니다.
def draw_vector_field(F, meshgrid):
vars = symbols('x y')
F_func = F.subs({key: value for key, value in zip((x, y,), vars)})
x_func = lambdify(vars, F_func.coeff(i), modules='numpy')
y_func = lambdify(vars, F_func.coeff(j), modules='numpy')
xx = meshgrid[0].flatten()
yy = meshgrid[1].flatten()
uu = x_func(*meshgrid).flatten()
vv = y_func(*meshgrid).flatten()
fig = ff.create_quiver(xx, yy, uu, vv)
fig.update_yaxes(
scaleanchor='x',
scaleratio=1,
)
fig.show()
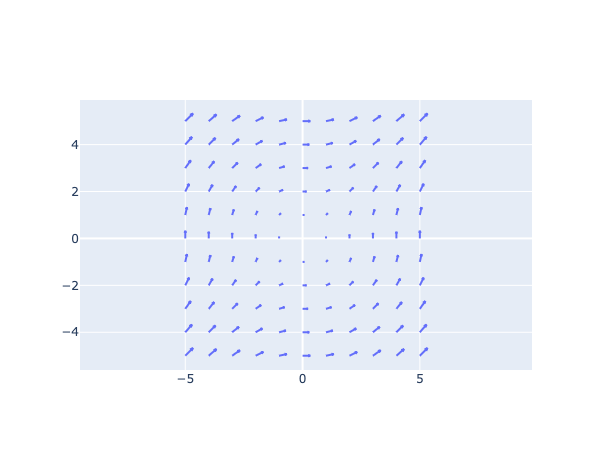
draw_vector_field(
log(1+y**2) * i + log(1+x**2) * j,
np.meshgrid(np.linspace(-5, 5, 11), np.linspace(-5, 5, 11))
)
선적분 (Line Integrals)
다음 문제를 해결하여 봅시다.
와 를 각각 다음과 같이 변수 ()로 매개화합니다.
따라서 선적분을 다음과 같이 기술할 수 있습니다.
from sympy.abc import t
x = cos(t)
y = sin(t)
f = 2 + x**2*y
integrate(f*sqrt(x.diff(t)**2 + y.diff(t)**2), (t, 0, pi))[출력 결과]
또는 벡터 기능을 사용하여...
x, y, z = N.x, N.y, N.z
x._latex_form = 'x'
y._latex_form = 'y'
z._latex_form = 'z'
f = 2 + x**2*y # 함수
region = ParametricRegion((cos(t), sin(t)), (t, 0, pi)) # 매개 곡선
vector_integrate(f, region)[출력 결과]
만일 구하고자 할 곡선이 반원이 아닌 원이라면, 또는 기타 primitive한 도형일 경우 도형을 불러오는 것도 가능합니다.
from sympy.geometry import Point, Circle
vector_integrate(f, Circle(Point(0, 0), 1)) # 중심이 원점인 단위원[출력 결과]
vector_integrate(f, Triangle(Point(-2, 3), Point(2, 3), Point(0, 5))) # (-2, 3), (2, 3), (0, 5)를 잇는 삼각형[출력 결과]
보존장 여부 확인하기
어떤 벡터장이 보존장(conservative field)인지 확인할 수 있습니다.
is_conservative((3 + 2*x*y) * i + (x**2 - 3*y**2) * j)[출력 결과]
Trueis_conservative((x - y) * i + (x - 2) * j)[출력 결과]
FalseScalar Potential 구하기
를 만족하는 를 구하고 싶을 경우 scalar_potential 함수를 이용합니다.
scalar_potential((3 + 2*x*y) * i + (x**2 - 3*y**2) * j, N)[출력 결과]
scalar_potential((y**2) * i + (2*x*y + exp(3*z)) * j + 3*y*exp(3*z) * k, N)[출력 결과]
만일 가 보존장이 아니라면 오류가 발생합니다.
scalar_potential((x - y) * i + (x - 2) * j, N) # ValueError: Field is not conservative