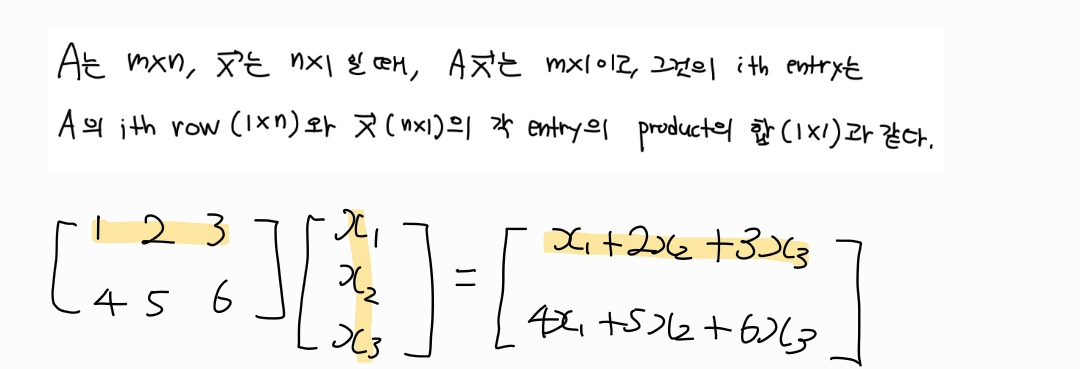[선형대수] 3-1. Vector Equations and Matrix Equation

Vectors in $\mathbf{R^2}$

다음과 같이 Column이 하나뿐인 벡터는 column vector, 또는 그냥 vector라고 부른다.

$\mathbf{w} = \begin{bmatrix} w_{1} \\ w_{2} \end{bmatrix}$

이처럼 두 개의 entries를 가지는 모든 vectors의 set을 $\mathbf{R^2}$이라고 한다(단, 각 entry는 real number). 즉 $\mathbf{v} \in \mathbf{R^2}$ 이다.

Vector Equations

벡터에 대해서 adding과 scaling이 가능하다. 단, 두 벡터를 더하려면 사이즈가 같아야 한다(둘 다 $\mathbf{R^n}$에 속해야 함).

Geometric Descriptions of $\mathbf{R^2}$

$\mathbf{R^2}$에 속하는 어떠한 벡터는 2차원 좌표평면에 표시할 수 있다. $\mathbf{v} = \begin{bmatrix} a \\ b \end{bmatrix}$ 일 때, $\mathbf{v}$는 원점으로부터 $(a, b)$라는 점을 가리키는 arrow로 표시될 수 있다.

또한 $\mathbf{R^2}$는 좌표평면의 모든 점의 집합과 같다.

Parallelogram Rule for Addition

$\mathbf{u}, \mathbf{v} \in \mathbf{R^2}$일 때, $\mathbf{R^2}$는 좌표평면에서 $\mathbf{u}, \mathbf{v}, \mathbf{0}$을 다른 세 꼭짓점으로 가지는 평행사변형의 꼭짓점에 해당한다.

Linear Combinations

벡터 $\mathbf{v_1}, ..., \mathbf{v_p} \in \mathbf{R^n}$ 과 스칼라 $\mathbf{c_1}, ..., \mathbf{c_p}$가 주어졌을 때, $\mathbf{y} = c_1\mathbf{v_1} + ... + c_p\mathbf{v_p}$ 를 만족하는 벡터 $\mathbf{y}$는 linear combination of $\mathbf{v_1}, ..., \mathbf{v_p}$ with weights $\mathbf{c_1}, ..., \mathbf{c_p}$라고 한다.

$\\$
Example)

$\mathbf{a_1}=\begin{bmatrix} 1 \\ -2 \\ -5 \end{bmatrix},$ $\mathbf{a_2}=\begin{bmatrix} 2 \\ 5 \\ 6 \end{bmatrix},$ $\mathbf{b}=\begin{bmatrix} 7 \\ 4 \\ -3 \end{bmatrix}$ 이라고 하자.
이때 $\mathbf{b}$가 $\mathbf{a_1}, \mathbf{a_2}$의 linear combination으로 표현될 수 있는지 알고 싶다면?
즉, $x_1\mathbf{a_1} + x_2\mathbf{a_2} = \mathbf{b}$로 표현했을 때 $x_1, x_2$라는 weights가 존재하는지 알고 싶다면?

=>

$x_1\begin{bmatrix} 1 \\ -2 \\ -5 \end{bmatrix} + x_2\begin{bmatrix} 2 \\ 5 \\ 6 \end{bmatrix} = \begin{bmatrix} 7 \\ 4 \\ -3 \end{bmatrix}$ 로 바꿔쓸 수 있고, 이는 곧

$\begin{bmatrix} x_1 + 2x_2 \\ -2x_1 + 5x_2 \\ -5x_1 + 6x_2 \end{bmatrix} = \begin{bmatrix} 7 \\ 4 \\ -3 \end{bmatrix}$ 과 같다. 이것은

$\begin{cases} x_1 + 2x_2 = 7 \\ -2x_1 + 5x_2 = 4 \\ -5x_1 + 6x_2 = -3 \end{cases}$ 이러한 system으로 표현할 수 있다.

이 system을 solve하려면? 앞서 배운 row reduction을 통해 augmented matrix의 REF를 구하면 된다. 그러면 $x_1 = 3, x_2 = 2$라는 해를 구할 수 있고, $\mathbf{b}$는 $\mathbf{a_1}$과 $\mathbf{a_2}$의 linear combination이라는 것을 알 수 있다.

이때, augmented matrix인

$\begin{bmatrix} 1 & 2 & 7\\ -2 & 5 & 4\\ -5 & 6 & -3\\ \end{bmatrix}$ 는 $\begin{bmatrix}\mathbf{a_1} & \mathbf{a_2} & \mathbf{b}\end{bmatrix}$ 로 표현될 수 있다(둘은 동일함).

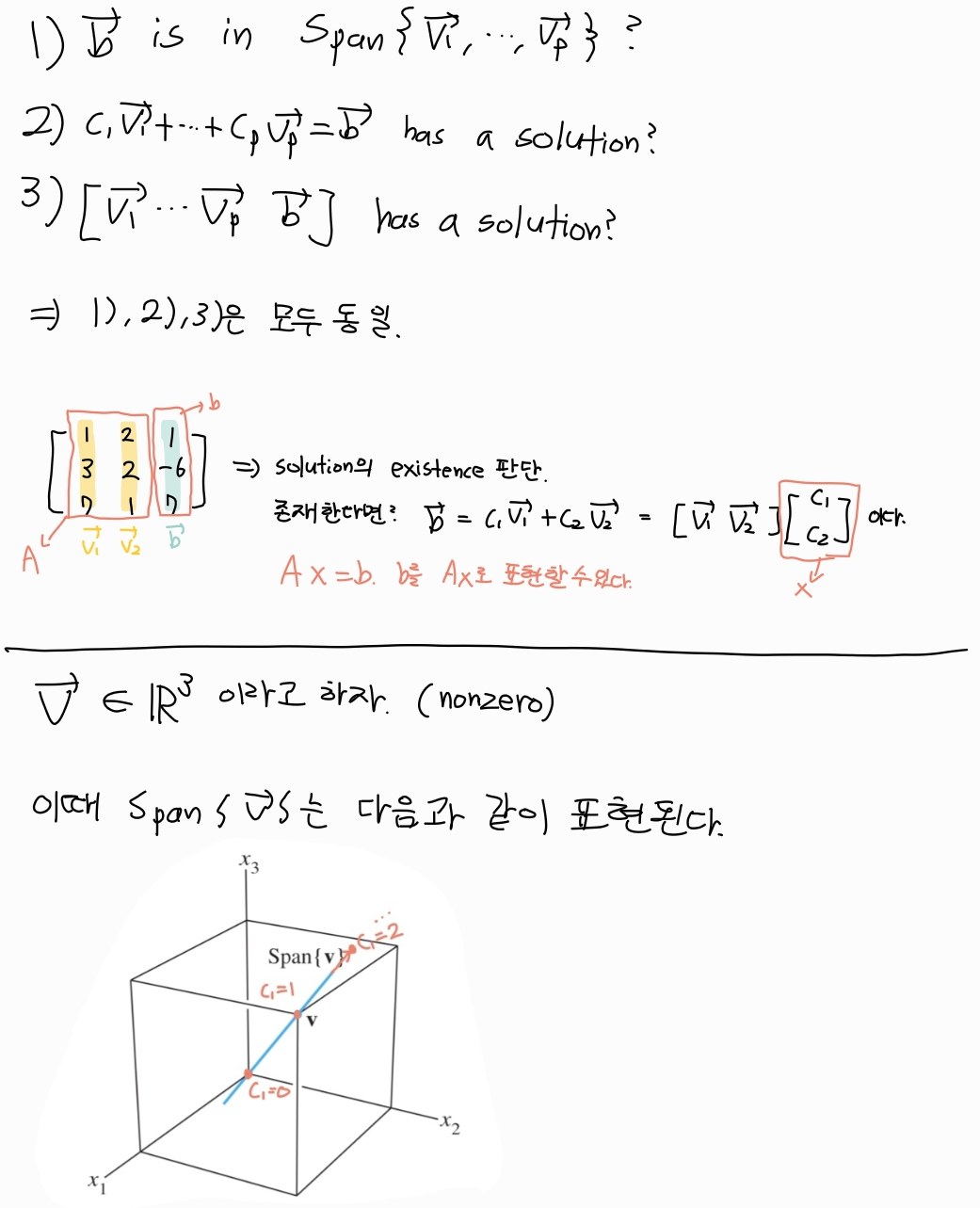
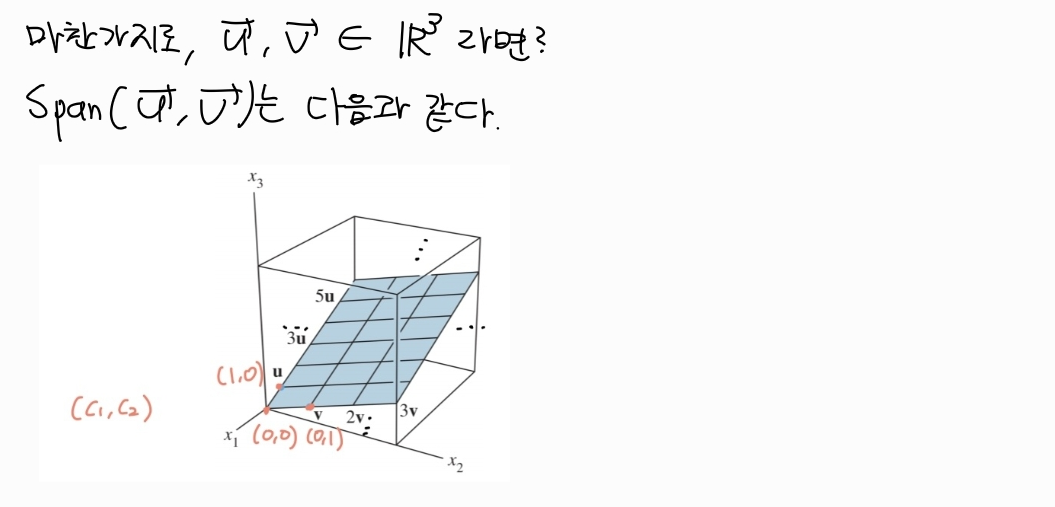
Span

$\mathbf{v_1}, ..., \mathbf{v_p} \in \mathbf{R^n}$ 일 때, 이들의 모든 linear combinations의 집합을 Span{$\mathbf{v_1}, ..., \mathbf{v_p}$}라고 한다.

Matrix Equation Ax = b

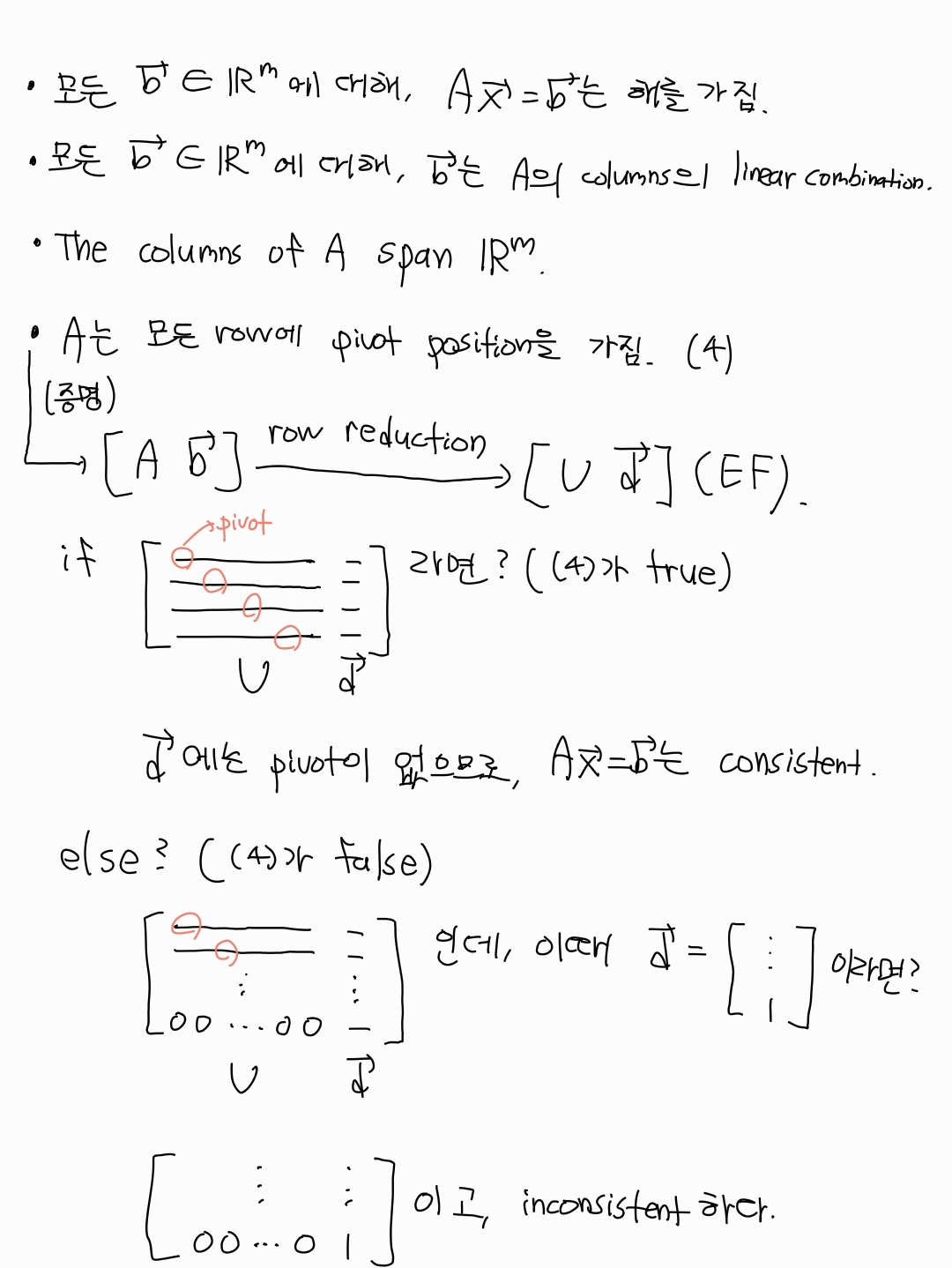
Existence of Solutions

A가 m*n matrix일 때, 다음 statements는 logically equivalent하다.

Row-Vector Rule for Computing Ax

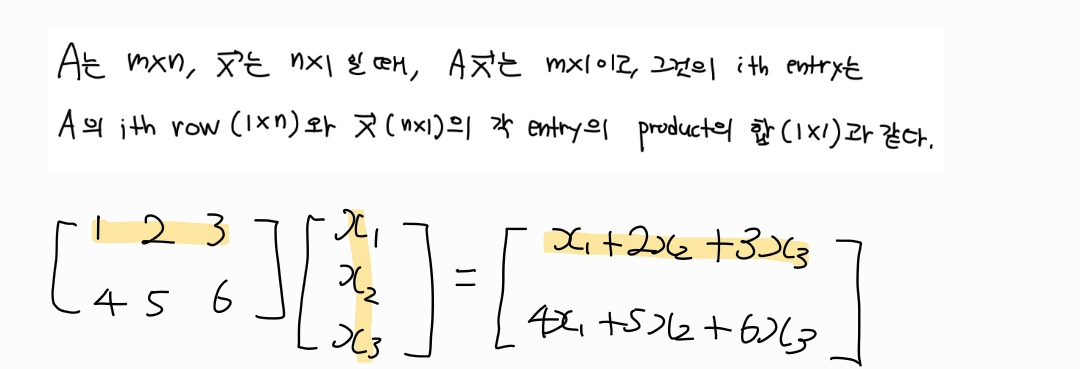
Identity Matrix