🎆백준 1260번 DFS와 BFS🎆
📌문제
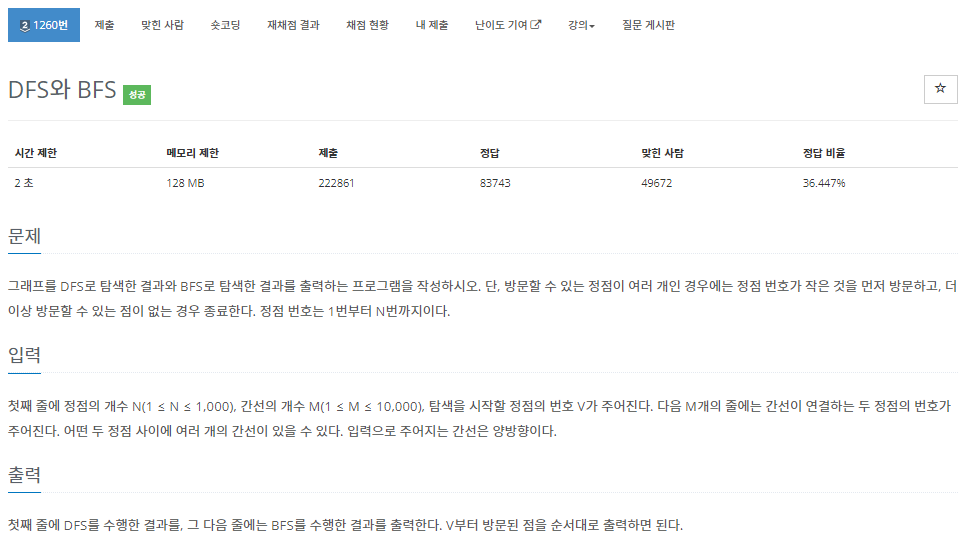
🔍문제 설명
문제 링크 : https://www.acmicpc.net/problem/1260
🔍예제 입력
4 5 1
1 2
1 3
1 4
2 4
3 4
🔍예제 출력
1 2 4 3
1 2 3 4
📌풀이
🔍풀이 설명
그래프 생성
linkedlist의 배열로 그래프를 선언했고, 노드의 수만큼 linkedlist를 생성했다. 그 후 간선은 양방향이므로 두 노드 모두에게 관계를 add해준다.
static LinkedList<Integer>[] Graph;
//LinkedList 로 graph 생성, 초기화
public static void graphLinkedList(int v){
Graph = new LinkedList[v+1];
for(int i=1; i<v+1; i++){
Graph[i] = new LinkedList<>();
}
}
//간선 추가 (양방향)
public static void addEdge(int v1, int v2){
Graph[v1].add(v2);
Graph[v2].add(v1);
}DFS
DFS 깊이 우선 탐색
DFS는 스택을 이용한 탐색 방법으로 정점(a)에서 시작하여 이웃하는 하나의 정점(b)을 방문하고, 방문한 정점(b)의 이웃 정점(c)을 방문하며, 더 이상 방문할 정점이 없다면 이전 정점으로 돌아와 방문하지 않은 이웃을 탐색하는 방법으로 깊이 우선으로 그래프를 탐색한다.
public static void DFS(int V, int N){
//DFS 깊이 우선 탐색 : Stack이용
Stack<Integer> stack = new Stack<>();
stack.push(V);
//방문여부 검사
boolean []visited = new boolean[N + 1];
//우선 모두 false로 초기화
Arrays.fill(visited, Boolean.FALSE);
//방문하는 요소
int w =0;
//스택에 요소가 있을 때만 수행
while(!stack.empty()) {
w = stack.pop(); //가장 마지막에 들어간 노드 하나 빼기
//방문하지 않았다면
if(!visited[w]) {
//노드 출력
System.out.print(w + " ");
//방문한 상태로 저장
visited[w] = true;
//정점 번호가 작은 것 먼저 방문해야하므로 FILO인 스택에서는 내림차순으로 정렬
Collections.sort(Graph[w], Collections.reverseOrder());
//노드에 연결된 노드들 수만큼 반복
for(int j=0; j<Graph[w].size(); j++) {
//노드 하나씩 가져와서
int g_node = Graph[w].get(j);
//방문 안한 상태면 스택에 넣어줌
if(!visited[g_node]) {
stack.push(g_node);
}
}
}
}
}BFS
BFS 너비 우선 탐색
BFS는 큐를 이용한 탐색 방법으로 정점(a)에서 시작해 정점(a)의 이웃하는 모든 정점(b), (c)... 을 방문하고, 방문한 정점들(b)의 이웃 정점들(d)..을 모두 방문하는 방식으로 그래프를 탐색한다.
public static void BFS(int V, int N){
//BFS 너비 우선 탐색 : Queue이용
Queue<Integer> queue = new LinkedList<>();
queue.add(V);
//방문여부 검사
boolean []visited = new boolean[N + 1];
//우선 모두 false로 초기화
Arrays.fill(visited, Boolean.FALSE);
//방문하는 요소
int w =0;
//큐에 요소가 있을 때만 수행
while(!queue.isEmpty()) {
w = queue.remove(); //가장 처음에 들어간 노드 하나 빼기
//방문하지 않았다면
if(!visited[w]) {
//노드 출력
System.out.print(w + " ");
//방문한 상태로 저장
visited[w] = true;
//정점 번호가 작은 것 먼저 방문해야하므로 FIFO인 큐에서는 오름차순으로 정렬
Collections.sort(Graph[w]);
//노드에 연결된 노드들 수만큼 반복
for(int j=0; j<Graph[w].size(); j++) {
//노드 하나씩 가져와서
int g_node = Graph[w].get(j);
//방문 안한 상태면 큐에 넣어줌
if(!visited[g_node]) {
queue.add(g_node);
}
}
}
}
}🔍전체 코드
package Graph;
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.*;
//DFS와 BFS
//graph 탐색 문제의 기본!
public class p1260 {
static LinkedList<Integer>[] Graph;
//LinkedList 로 graph 생성, 초기화
public static void graphLinkedList(int v){
Graph = new LinkedList[v+1];
for(int i=1; i<v+1; i++){
Graph[i] = new LinkedList<>();
}
}
//노드 추가 (양방향)
public static void addEdge(int v1, int v2){
Graph[v1].add(v2);
Graph[v2].add(v1);
}
public static void DFS(int V, int N){
//DFS 깊이 우선 탐색 : Stack이용
Stack<Integer> stack = new Stack<>();
stack.push(V);
//방문여부 검사
boolean []visited = new boolean[N + 1];
//우선 모두 false로 초기화
Arrays.fill(visited, Boolean.FALSE);
//방문하는 요소
int w =0;
//스택에 요소가 있을 때만 수행
while(!stack.empty()) {
w = stack.pop(); //가장 마지막에 들어간 노드 하나 빼기
//방문하지 않았다면
if(!visited[w]) {
//노드 출력
System.out.print(w + " ");
//방문한 상태로 저장
visited[w] = true;
//정점 번호가 작은 것 먼저 방문해야하므로 FILO인 스택에서는 내림차순으로 정렬
Collections.sort(Graph[w], Collections.reverseOrder());
//노드에 연결된 노드들 수만큼 반복
for(int j=0; j<Graph[w].size(); j++) {
//노드 하나씩 가져와서
int g_node = Graph[w].get(j);
//방문 안한 상태면 스택에 넣어줌
if(!visited[g_node]) {
stack.push(g_node);
}
}
}
}
}
public static void BFS(int V, int N){
//BFS 너비 우선 탐색 : Queue이용
Queue<Integer> queue = new LinkedList<>();
queue.add(V);
//방문여부 검사
boolean []visited = new boolean[N + 1];
//우선 모두 false로 초기화
Arrays.fill(visited, Boolean.FALSE);
//방문하는 요소
int w =0;
//큐에 요소가 있을 때만 수행
while(!queue.isEmpty()) {
w = queue.remove(); //가장 처음에 들어간 노드 하나 빼기
//방문하지 않았다면
if(!visited[w]) {
//노드 출력
System.out.print(w + " ");
//방문한 상태로 저장
visited[w] = true;
//정점 번호가 작은 것 먼저 방문해야하므로 FIFO인 큐에서는 오름차순으로 정렬
Collections.sort(Graph[w]);
//노드에 연결된 노드들 수만큼 반복
for(int j=0; j<Graph[w].size(); j++) {
//노드 하나씩 가져와서
int g_node = Graph[w].get(j);
//방문 안한 상태면 큐에 넣어줌
if(!visited[g_node]) {
queue.add(g_node);
}
}
}
}
}
public static void main(String[] args)throws Exception{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
//정점수
int N = Integer.parseInt(st.nextToken());
//간선수
int M = Integer.parseInt(st.nextToken());
//탐색을 시작할 정점의 번호
int V = Integer.parseInt(st.nextToken());
//그래프 생성
graphLinkedList(N);
for(int i=0; i<M; i++){
st = new StringTokenizer(br.readLine());
int v1 = Integer.parseInt(st.nextToken());
int v2 = Integer.parseInt(st.nextToken());
addEdge(v1, v2);
}
DFS(V, N);
System.out.println();
BFS(V, N);
}
}
👋마무리👋
dfs, bfs는 중요한 알고리즘이라고 들었는데 이번 문제 풀이를 통해 기본 로직을 구현할 수 있어서 좋았다.! 앞으로 깊이 우선, 너비 우선 탐색을 이용한 문제를 풀 때 이 글을 참고하면 좋을 것 같다!! ㅎㅎ

