[ Algorithm ] 백준 2805번 : 나무 자르기 - [JAVA]

Minsu Lee·2023년 3월 1일

Java algorithm

baekjoon

목록 보기

14/16

🎆백준 2805번 나무 자르기🎆

📌문제

🔍문제 설명

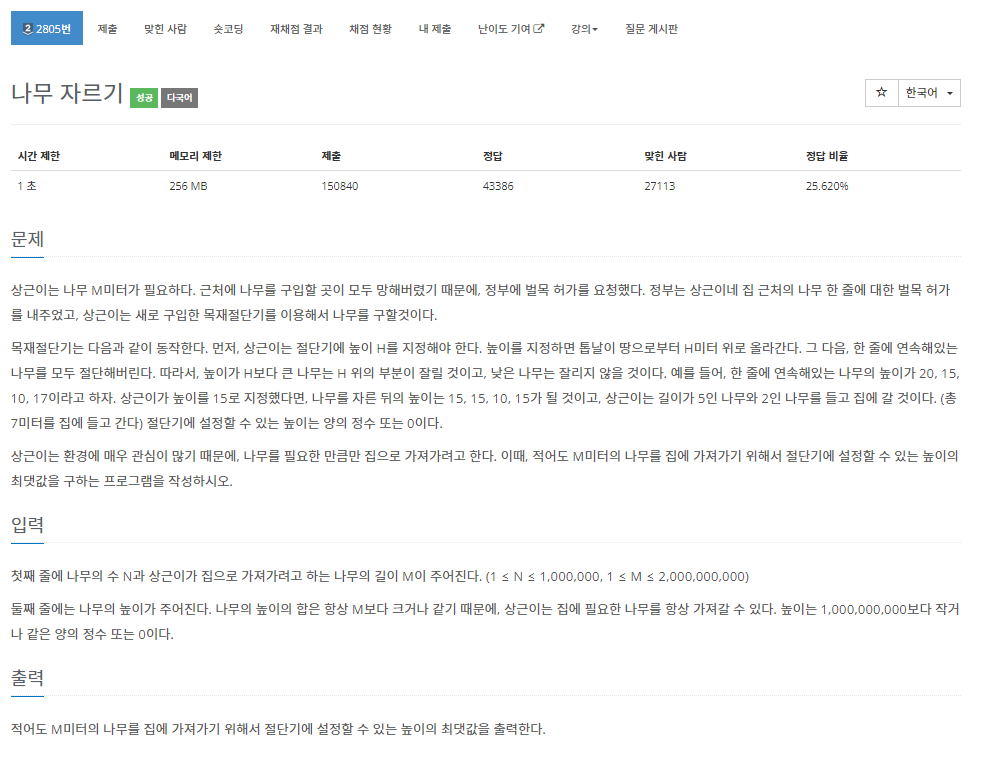
문제 링크 : https://www.acmicpc.net/problem/2805

🔍예제 입력

4 7
20 15 10 17

🔍예제 출력

15

📌풀이

🔍풀이 설명

이분 탐색(Binary Search)을 이용한 문제였다.

이분탐색 (Binary Search) : 이진 탐색(이분 탐색) 알고리즘은 정렬되어 있는 리스트에서 탐색 범위를 절반씩 좁혀가며 데이터를 탐색하는 방법이다.

이진 탐색은 정렬된 데이터를 이용해 탐색하는 방법이므로 탐색하고자 하는 리스트, 배열 내부의 데이터가 정렬되어 있어야만 사용할 수 있는 알고리즘이다.

변수 3개(start, end, mid 혹은 min max, mid 등)를 사용하여 탐색한다. 찾으려는 데이터와 중간점 위치에 있는 데이터를 반복적으로 비교해서 원하는 데이터를 찾는 것이 이진 탐색의 과정이다.

이 문제에서 구해야할 것은 절단기에 설정할 길이이므로 절단기에 설정할 길이가 이분 탐색에서 이용되어야 한다. 이진 탐색 구조는 다음과 같다.

길이에서 최대값(max)은 주어진 나무의 길이중 최대값+1로 설정하고 최소값(min)은 0으로 시작한다.
mid = (min+max)/2로 설정한 후 tree의 길이에서 잘라진 나무의 길이의 합을 구한다.
M과 H를 비교해 H<M이면 max = mid로 설정해 잘라지는 길이가 더 증가하도록 설정하고 아닌 경우 min = mid+1로 잘라지는 길이가 더 줄어들도록 설정한다.
위의 과정을 min<max인 경우 반복한다.

주의할 점 데이터의 크기(잘랐을 때 구해지는 길이..)가 int의 범위를 넘을 수 있으므로 long으로 설정하고 실행한다.

🔍코드

package Binary_Search;

import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.StringTokenizer;

//나무 자르기
public class p2805 {
    public static void main(String[] args)throws Exception{
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(br.readLine());

        int N = Integer.parseInt(st.nextToken());
        long M = Integer.parseInt(st.nextToken());

        long tree[] = new long[N];
        long max = Integer.MIN_VALUE;
        st = new StringTokenizer(br.readLine());

        for(int i=0; i<N; i++) {
            long number = Long.parseLong(st.nextToken());
            tree[i] = number;
            if (max < number) {
                max = number;
            }
        }
        //절단기 설정 길이 값을 최대길이 +1로 잡아야함
        max++;
        long min = 0;
        long mid = 0;
        //절단기에 설정하는 길이 자체를 가지고 binary search..

        while(min < max){
            mid = (max+min) / 2;

            long H=0;   //잘랐을 때 구해지는 길이
            for(int i=0; i<N; i++){
                if(tree[i]- mid > 0){
                    H += (tree[i]-mid);
                }
            }
            //구해진 길이가 원하는 길이보다 작을 경우 잘라지는 길이가 많아지도록 max를 줄인다
            if(H < M){
                max = mid;
            }
            //구해진 길이가 원하는 길이보다 클 경우 잘라지는 길이가 줄어들도록 min값을 늘린다.
            else{
                min  = mid + 1;
            }
        }
        System.out.print(min-1);
    }
}