[다이나믹 프로그래밍]정수 삼각형-파이썬

문제

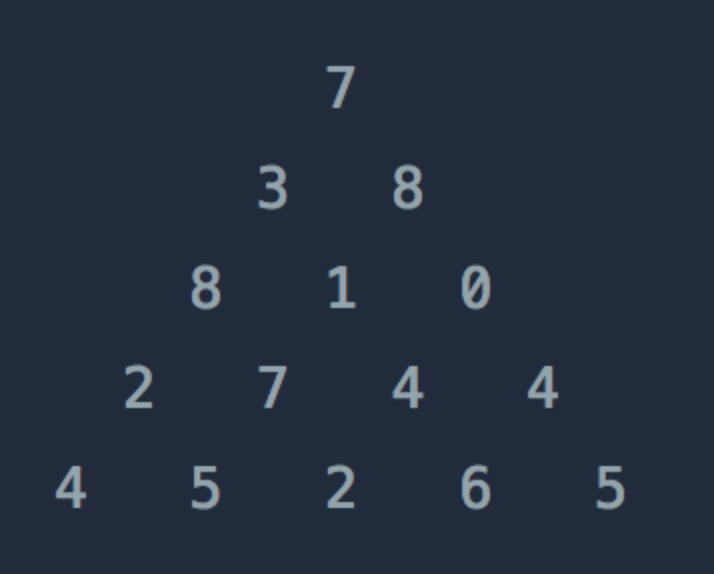
위와 같은 삼각형의 꼭대기에서 바닥까지 이어지는 경로 중, 거쳐간 숫자의 합이 가장 큰 경우를 찾아보려고 합니다. 아래 칸으로 이동할 때는 대각선 방향으로 한 칸 오른쪽 또는 왼쪽으로만 이동 가능합니다. 예를 들어 3에서는 그 아래칸의 8 또는 1로만 이동이 가능합니다.

삼각형의 정보가 담긴 배열 triangle이 매개변수로 주어질 때, 거쳐간 숫자의 최댓값을 return 하도록 solution 함수를 완성하세요.

제한 조건

• 삼각형의 높이는 1 이상 500 이하입니다.
• 삼각형을 이루고 있는 숫자는 0 이상 9,999 이하의 정수입니다.

입출력 예

triangle	result
[[7], [3, 8], [8, 1, 0], [2, 7, 4, 4], [4, 5, 2, 6, 5]]	30

풀이

def solution(triangle):
    #memoization을 위한 depth
    depth = []
    #triangle 길이 만큼 빈배열로 초기화
    for _ in range(len(triangle)):
        depth.append([])
    depth[0].append(triangle[0][0])
    for i in range(1,len(triangle)):
        for j in range(i+1):
            #맨 왼쪽은 전  depth[전단계][0]에서 현재 triangle더하기
            if j == 0:
                depth[i].append(depth[i-1][0]+triangle[i][j])
            #맨 오른쪽은 depth[전단계][j-1]에서 현재 triangle더하기
            elif j == i:
                depth[i].append(depth[i-1][j-1]+triangle[i][j])
            #중간인 경우 depth[전단계][j-1]과 depth[전단계][j] 중에 큰 수를 현재 triangle에 더하기
            else:
                depth[i].append(max(depth[i-1][j-1],depth[i-1][j])+triangle[i][j])
    #가장 아래층에서 가장 큰수 구해서 return
    return max(depth[len(depth)-1])
print(solution([[7], [3, 8], [8, 1, 0], [2, 7, 4, 4], [4, 5, 2, 6, 5]]))

💡TIL

처음에는 각 자리까지 오는 모든 경우의 수를 다 구해서 하려고 했다.
예) depth[2]에[10,[11,16],15]
한번 푼것은 memoization에 저장하고 다시 풀지 않는것이 다이나믹 프로그래밍의 정의이다. 각 자리까지 오는 모든 경우의 수를 저장 할 필요 없이 해당 자리에서의 해를 구하면 되는것이다.