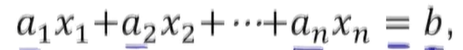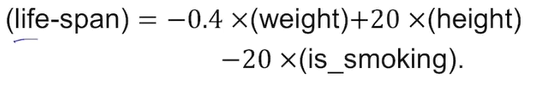선형방정식, 선형시스템

선형방정식

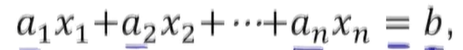
• 상수와 confficients a1..an으로 한다

선형시스템

• linear 방정식의 집합

예시

• 대문자 A는 메트릭이며 계수들을 모아 놓은 것
• 몸무게 키 흡연여부를 x인 가중치 벡터에 모아 놓는다
• b는 결과들을 벡터로 모아놓은 것

• 간단하게 이렇게 표현이 가능

Identity Matrix

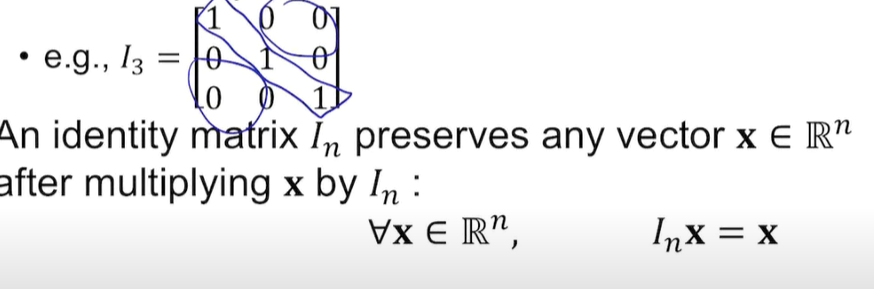
• 항등행렬이란 가운데 있는 값들이 1이고 나머지는 0
• 항등행렬은 어떤 벡터랑 곱해져도 자기 자신의 값을 나타내기 때문

Inverse Matrix

• square matrix 정사각형 메트릭만을 대상으로 한다
• 역행렬은 정사각 행렬에서만 존재
• 직사각행렬에서는 둘중에 한쪽의 메트릭스만 만족(둘다 만족 안된다)
  
• 계수 A의 역행렬을 구해서 x(가중치)를 구할 수 있다.

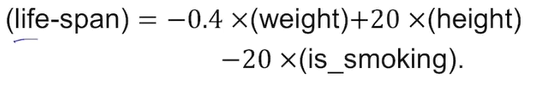
• 역행렬을 통해 구한 x를 통해 입력값들을 곱하고 life-span을 구할 수 있다

Non-Invertible Matrix A for Ax = b

• 역행렬이 존재하지 않는다는 것은 2by2에서는 ad-bc가 0이 된다(det A determinant A라고 한다)
  • a : b = c : d일 경우 역행렬이 존재하지 않는다
• 해가 없거나 무수하게 많아진다

Does a Matrix Have an Inverse Matrix

• 벡터들의 확대 및 축소의 배율을 생각할 수 있다

Rectangular Matrix A in Ax = b

• 데이타수보다 feature의 수가 더 많은 경우
• feaure수보다 데이터수가 많은경우 Regularization를 사용