연쇄행렬곱셈

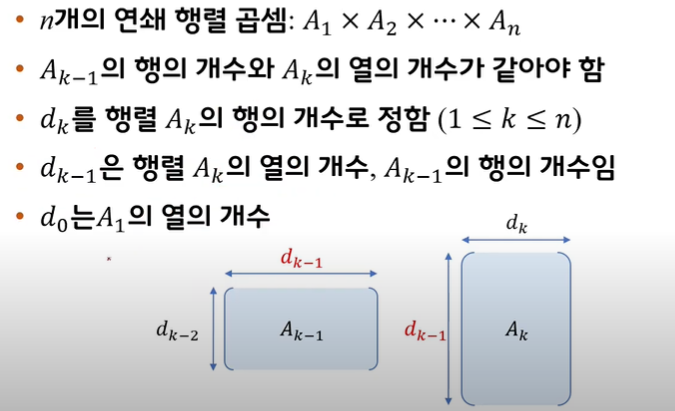
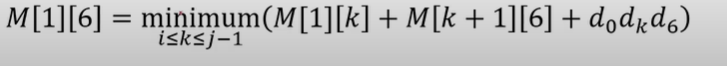연쇄 행렬 곱셈

• 각 원소의 곱셈 횟수가 가장 작아지도록 하는 곱셈 순서가 최적의 순서

최적화 문제

• 원소의 곱셈 횟수를 최소화하는 행렬 곱셈의 순서 찾기

문제의 이해

• 2x3행렬과 3x4행렬 곱하면 2x4나온다.
  • 2x3x4 = 24가 곱하는 횟수이다.

문제의 정의

연쇄 행렬 곱셈(DP)

1단계: 재귀 관계식

• M: 연쇄 행렬을 곱하는데 필요한 곱셈의 최소 회수 행렬
• M[i][j]: A(i~j)까지 행렬을 곱하는데 필요한 곱셈의 최소 회수(1<=i<=j<=n)
• 목표 A(i~j) 행렬을 A(i~k)A(k+1~j)로 분할하는 재귀 관계식 찾기

2단계: 상향식 방법으로 해답을 구한다

• 초기화 M[i][j] = 0(주대각선을 0으로)
• 최종목표: M[1][n]
• 상향식 계산: 대각선1번,...,대각선 n-1번

재귀 관계식

• 분할정복
  n개의 행렬을 두개의 최적 부분행렬의 곱으로 분할
• 6개일 경우 5개로 분할 가능:
  
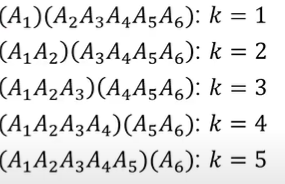
• 각 분할의 곱셈 횟수:
  • 각 부분행렬의 곱셈횟수 + 두 행렬의 곱셈횟수
  • M[1][k] + M[k+1][6]+ d0xdkxd6
• 최적분할
  •