순차탐색 : 리스트 안에 있는 특정한 데이터를 찾기 위해 앞에서 부터 하나씩 확인
이진탐색 : 정렬되어 있는 리스트에서 탐색 범위를 절반씩 좁혀가며 데이터를 탐색 (시작점, 끝점, 중간점을 이용하여 탐색 범위 설정)
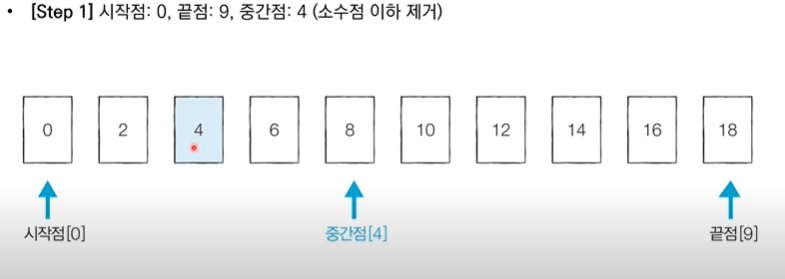
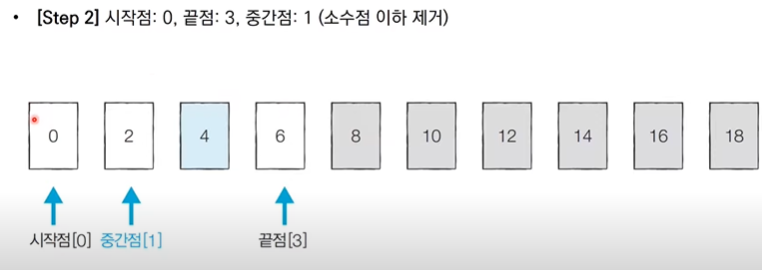
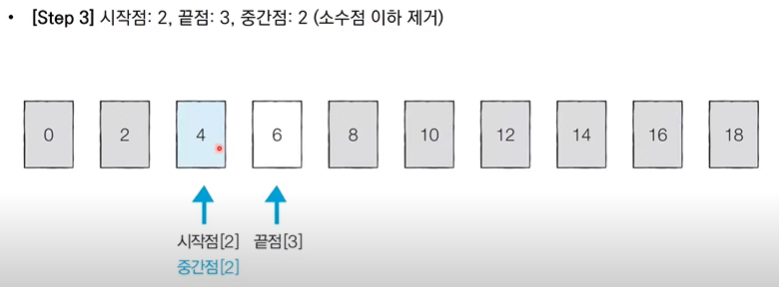
단계마다 탐색 범위를 2로 나누는 것과 통일하다
이는 logN에 비례한다
O(logN)
파이썬 이진탐색 라이브러리
bisect_left(a,x): 정렬된 순서를 유지하면서 배열 a에 x를 삽입할 가장 왼쪽 인데스를 반환
bisect_right(a,x): 정렬된 순서를 유지하면서 배열 a에 x를 삽입할 가장 오른쪽 인덱스를 반환
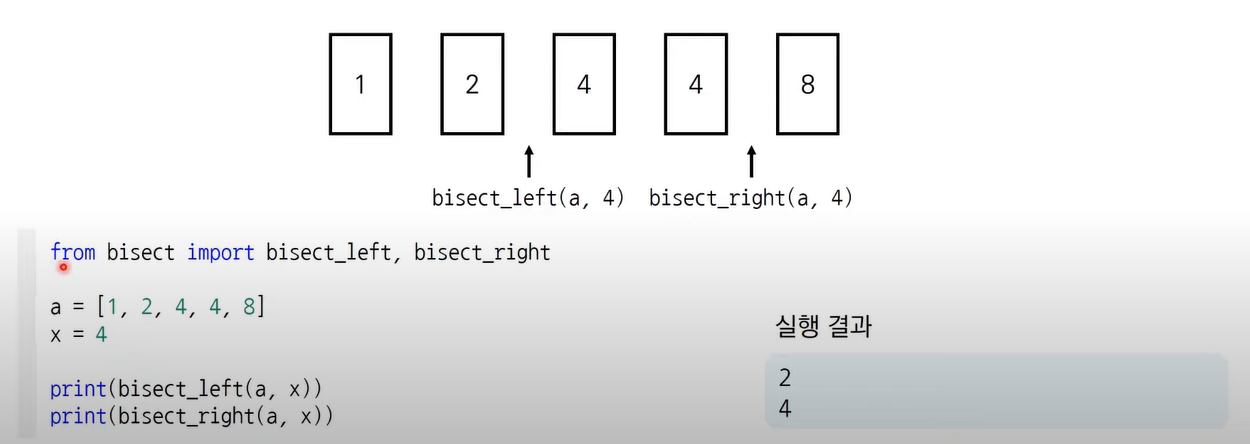
from bisect import bisect_left, bisect_right
#값이 [left_value, right_value]인 데이터의 개수를 반환하는 함수
def count_by_range(a, left_value, right_value):
right_index = bisect_right(a, right_value)
left_index = bisect_left(a, left_value)
return right_index - left_index
#배열 선언
a = [1,2,3,3,3,3,4,4,8,9]
#값이 4인 데이터 개수 출력
print(count_by_range(a,4,4))
#값이 [1,3] 범위에 있는 데이터 개수 출력
print(count_by_range(a,1,3))파라메트릭 서치
최적화 문제를 결정 문제('예' 혹은 '아니오')로 바꾸어 해결
Ex) 특정한 조건을 만족하는 가장 알맞은 값을 빠르게 찾는 최적화 문제
Ex) 떡볶이 문제

조건의 만족 여부("예" 혹은 "아니오")에 따라서 탐색 범위를 좁혀서 해결 가능
큰 탐색 범위를 보면 가장 먼저 이진탐색을 떠올려야한다.
Step1
시작점:0, 끝점:19, 중간점:9
이때 필요한 떡 크기 M=6이므로 결과 저장
잘린떡(10,6,1,8)
Step2
시작점:10, 끝점:19, 중간점:14
이때 필요한 떡 크기 M=6이므로 결과 저장
잘린떡(5,1,0,3)
Step3
시작점:15, 끝점:19, 중간점:17
이때 필요한 떡 크기 M=6이므로 결과 저장하지 않음
잘린떡(2,0,0)
Step4
시작점:15, 끝점:16, 중간점:15
이때 필요한 떡 크기 M=6이므로 결과 저장
Ex)

Ex)
전자 매장에는 부품이 N개 있고, 각 부품은 정수 형태의 고유한 번호가 있다. 부품 M개 종류가 모두 있는지 확인하는 프로그램을 작성해보자.
입력 예시
5
8 3 7 9 2
3
5 7 9
출력 예시
no yes yes