최단 경로 알고리즘

최단경로

가장 짧은 경로를 찾는 알고리즘

• 문제 상황
  • 한 지점에서 다른 한 지점까지의 최단 경로
  • 한 지점에서 다른 모든 지점까지의 최단 경로
  • 모든 지점에서 다른 모든 지점까지의 최단 경로
• 각 지점은 그래프에서 노드로 표현
• 지점 간 연결된 도로는 그래프에서 간선으로 표현
  

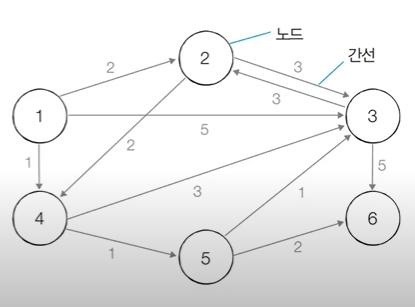
다익스트라 최단 경로 알고리즘

• 특정한 노드에서 출발하여 다른 모든 노드로 가는 최단 경로 계산
• 다익스트라 최단 경로 알고리즘은 간선이 없을 때 정상적 동작
  • 현실 세계의 도로(간선)은 음의 간선으로 표현되지 않습니다.
• 다익스트라 최단 경로 알고리즘은 그리디 알고리즘으로 분류
  • 매 상황에서 가장 비용이 적은 노드를 선택해 임의의 과정 반복

다익스트라 동작 과정

1. 출발 노드를 설정
2. 최단 거리 테이블을 초기화
3. 방문하지 않은 노드 중에서 최단 거리가 가장 짧은 노드를 선택
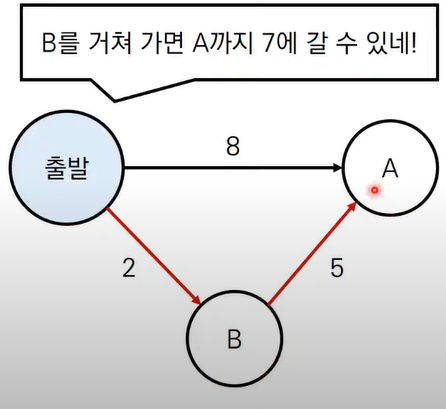
4. 해당 노드를 거쳐 다른 노드로 가는 비용을 계산하여 최단 거리 테이블을 갱신
5. 위 과정에서 3,4번 반복

• 알고리즘 동작 과정에서 최단 거리 테이블은 각 노드에 대한 현재까지의 최단 거리 정보를 가지고 있다.
• 처리 과정에서 더 짧은 경로를 찾으면 '이제부터는 이 경로가 더 짧다.'라고 갱신
  

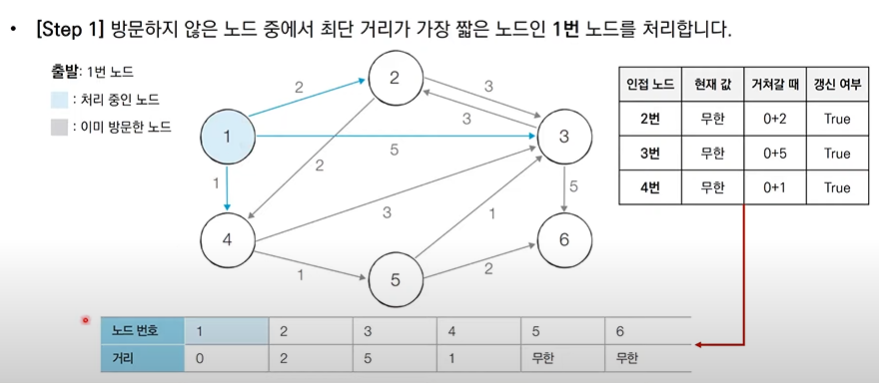
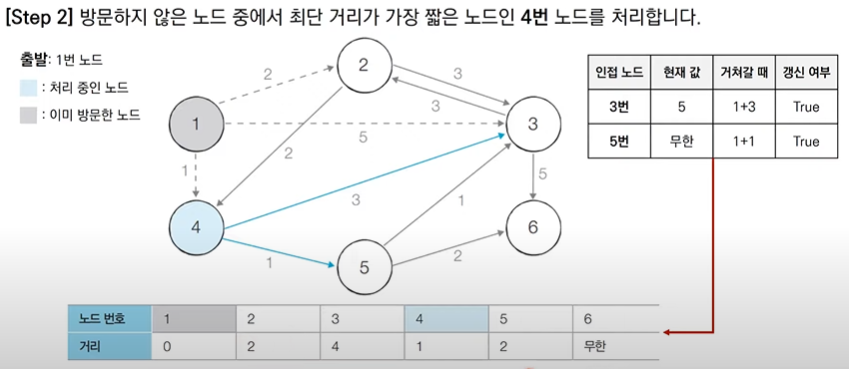
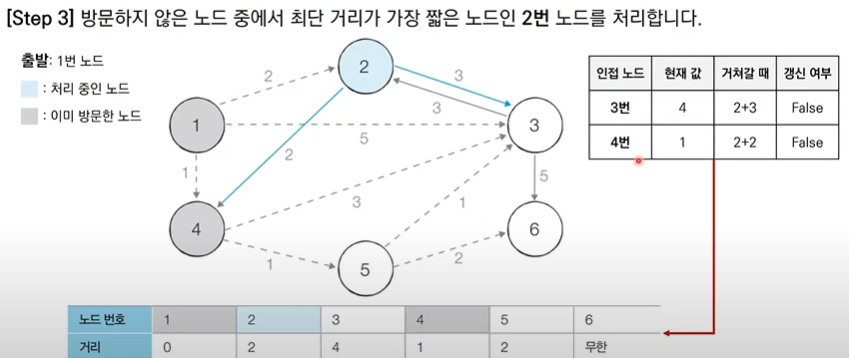
(Step3)
이미 방문 처리된거는 최단거리가 결정되었기 바뀌지 않기 때문에 무시할 수 있다.

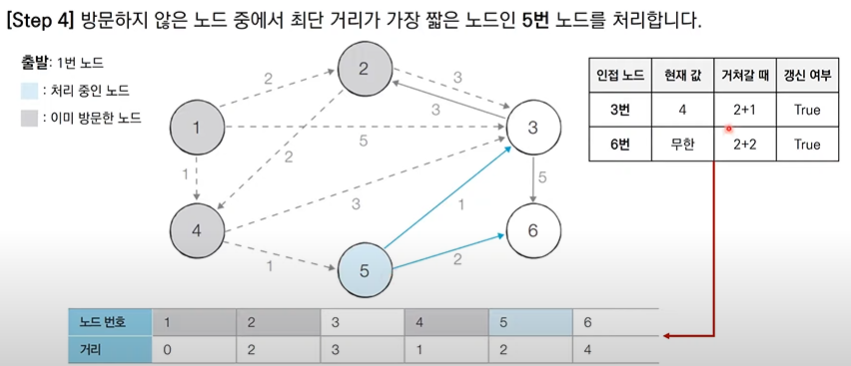
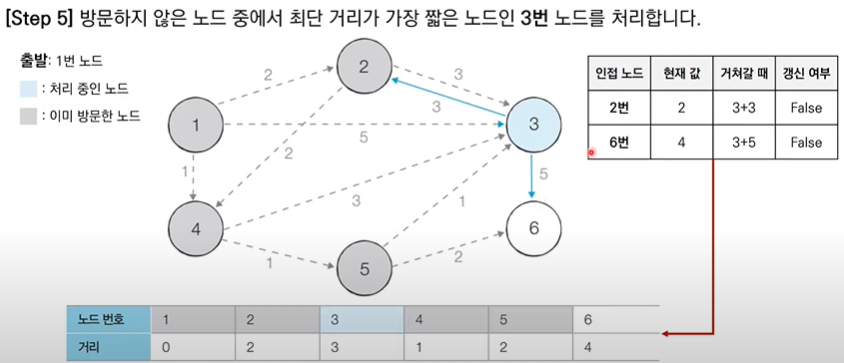
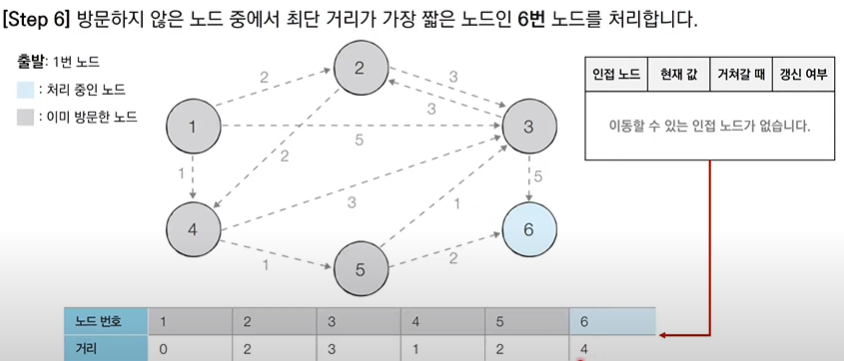
다익스트라 알고리즘 특징

• 그리디 알고리즘: 매 상황에서 방문하지 않은 가장 비용이 적은 노드를 선택해 임의의 과정을 반복
• 단계를 거치며 한 번 처리된 노드의 최단 거리는 고정되어 더 이상 바뀌지 않음
  • 한 단계당 하나의 노드에 대한 최단 거리를 확실히 찾는 것으로 이해할 수 있다.
• 다익스트라 알고리즘을 수행한 뒤에 테이블에 각 노드까지의 최단거리 정보가 저장
  • 완벽한 형태의 최단 경로를 구하려면 소스코드에 추가적인 기능을 더 넣어야 함
• 단계마다 방문하지 않은 노드 중에서 최단 거리가 가장 짧은 노드를 선택하기 위해 매 단계마다 1차원 테이블의 모든 원소를 확인(순차 탐색) 합니다.