평범한 배낭(12865)

배낭채우기 문제

• 보석을 자를 수 있다고 가정하는 Fractional Knapsack (greedy)
• 보석을 자를 수 없다는 0-1 knapsack문제가 있다.(Dp)

기본적으로 (Dynamic Programming: DP)방법을 쓰는 기본적인 문제로 알려짐

1) 모든 경우의 수를 넣어본다.(Brute-Force)

• n개의 보석이 있다고 치면, n개 보석으로 만들 수 있는 가능한 부분집합의 수는 2^n개이다.(들어있거나 안들어있거나) 최악의 경우 2^n번 까지 봐야하는 O(2^n)알고리즘이다.

2) 가격이 높은 보석, 혹은 (가격/무게)의 값이 제일 높은 보석부터 먼저 골라 넣는다.

• 무게당 가치를 계산해서 제일 높은 것부터한다.
• 특정한 기준을 정해놓고 그 기준의 값이 높은 순으로 집는 걸 그리디알고리즘
• 이경우는 분할할 수 있는경우에 가능하다.(Fractional Knapsack)

다이나믹과 그리드 차이

다이나믹

• 다이나믹은 모든 부분 문제를 풀어 항상 최적의 답을 구한다.
  • 최단거리 예제에서는, 가능한 모든 길을 다 살핀 후 그중 최단거리 길 선택
  • 모든 부분문제를 풀기 때문에 전체 문제의 크기가 클수록, 가능한 선택의 경우가 많을 수록 최적해를 찾는데 많은 메모리와 시간이 소요

그리드

• 모든 문제를 풀지 않는다.
• 선택이 필요할 때 마다 이후의 상황은 고려하지 않고 그떄의 최선인 선택
• 속도면에서 다이나믹보다 빠르다.

응용문제 해결

그리드의 경우

• 각 요소들을 특정 기준으로 정렬
• 정렬한 요소들을 훑으며 부분 문제들을 해결하면서 결과적으로 전체문제 해결

DP

• 큰 문제를 작은 문제로 쪼개서 해결, 이전에 계산해둔 값을 메모리에 저장해서 반복작업을 줄이는 기법
• 집합 A를 n개의 보석들 중에서 최적으로 고른 부분집합이라 가정
  • 집합 A가 n번째 보석을 포함하고 있지 않다면 A는 n번째 보석을 뺀 나머지 n-1개의 보석들 중에서 최적으로 고른 부분집합과 같다.
  • 집합 A가 n번째 보석을 포함하고 있다면 A에 속한 보석들의 총 가격은 n-1개의 보석들 중에서 최적으로 고른 가격의 합에다가 보석 n의 가격을 더한것과 같다.
    (단, n번째 보석을 넣었을 때 배낭이 터지지 않아야 한다.)

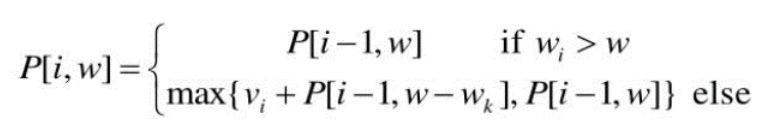
• P[i,w] 란 i개의 보석이 있고 배낭의 무게 한도가 w일 때 최적의 이익을 의미

  • i번째 보석이 배낭의 무게 한도보다 무거우면 넣을 수 없으므로 i번째 보석을 뺀 i-1개의 보석들을 가지고 구한 전단계의 최적값을 그대로 가져온다.
  • 그렇지 않은 경우, i번째 보석을 위해 i번째 보석만큼의 무게를 비웠을 떄의 최적값에 i번째 보석의 가격을 더한 값 or i-1개의 보석들을 가지고 가지고 구한 전 단계의 최적값 중 큰 것을 선택

• P라는 2차원 리스트를 채워나가면서, 필요한 경우 "앞에서 계산했던 다른 칸의 값을 이용해서" 다음 칸의 값을 계산

보완1

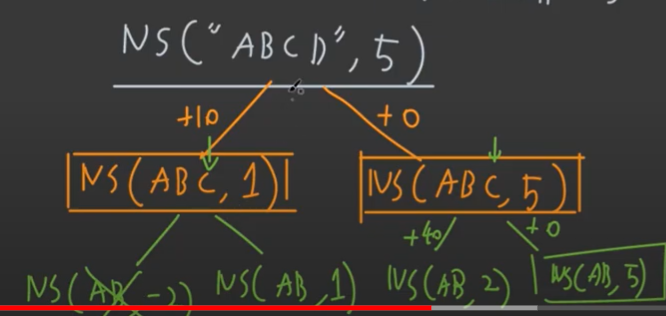
• Problem ("abcd",5)
  SubProblem: d가 있는경우 없는경우

• c가 있는경우 없는경우

• 이런식으로 계속 진행

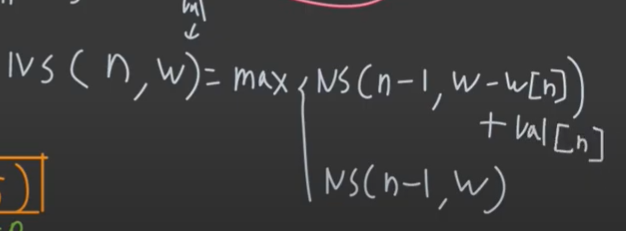
• 점화식으로 표현하면 처음 n개에서 d가 있는 경우 없는경우 둘다 -1하고 있는경우 ns(개수-1, 처음무게-없는 d의 무게)+그것의 가치
• 다른 하나는 ns(n-1,w)

보완2

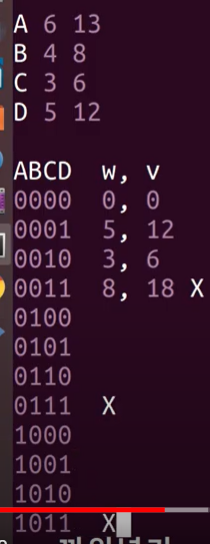
• 모든 경우를 써보자 그리고 0011의 무게가 7을 넘는 순간 0111 1011다 X다
  즉, 0011부터는 계산을 할 필요가 없다. 이런식으로 나머지도

• 1000부터는 0000~0111구한거에 더하면 된다.
  

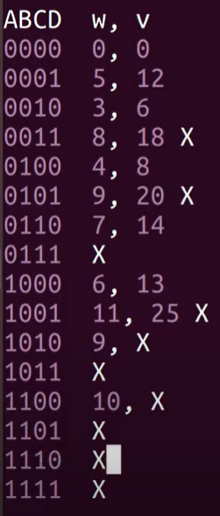
• weight에 테이블 대해서 가치를 관리하면 될꺼같다.

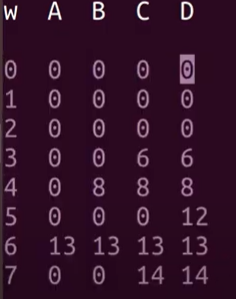
• 넣을 때 뺄 때 다하면 2^n이 될텐데 해볼필요가 없는 경우도 있으므로 제외해줄 방법을 생각하다가 weight에 대한 테이블로 만들면 그 이상의 값인 것들은 무시하면 된다.

결국 복잡성은 개수(한계값)x무게(한계값)

보완3

그리디로 하기 힘든 이유

• 무게가 작은 순으로 넣어보기
  • 1kg/1, 2kg/1, 3kg/2, 4kg/2 가치합은 6이된다.
  • 만약 5kg/10이라 한다면 가치가 더 크다.
• 가치가 큰 순으로 넣어보기
  • 10kg/10, 1kg/9, 2kg/5
  • 이 경우에도 1+3kg의 가치가 더 큰데 10kg에서 끝남

결국 모든 경우의 수를 해봐야 한다.